
Рефераты по рекламе
Рефераты по философии
Рефераты по финансам
Рефераты по химии
Рефераты по цифровым устройствам
Рефераты по экологическому праву
Рефераты по экономико-математическому моделированию
Рефераты по экономической географии
Рефераты по экономической теории
Рефераты по этике
Рефераты по юриспруденции
Рефераты по языковедению
Рефераты по юридическим наукам
Рефераты по истории
Рефераты по компьютерным наукам
Рефераты по медицинским наукам
Рефераты по финансовым наукам
Рефераты по управленческим наукам
Рефераты по строительным наукам
Психология педагогика
Промышленность производство
Биология и химия
Языкознание филология
Издательское дело и полиграфия
Рефераты по краеведению и этнографии
Рефераты по религии и мифологии
Рефераты по медицине
Рефераты по сексологии
Рефераты по москвоведению
Рефераты по экологии
Краткое содержание произведений
Рефераты по физкультуре и спорту
Топики по английскому языку
Рефераты по математике
Рефераты по музыке
Остальные рефераты
Шпаргалка: Математические модели в естествознании
Шпаргалка: Математические модели в естествознании
Вопросы экзамена
1. Основные понятия и определения генетики.
2. Законы Менделя
3. Закон Харди- Вайнберга
4. Принцип стационарности. Кадрильный закон. Неизбежность концепции гена. Вопрос о группах крови.
5. Инбридинг.
6. Сцепление и кроссинговер.
7. Наследование признаков, сцепленных с полом.
8. Отбор в менделевской бесполой диплоидной популяции.
9. Исследование эволюционных уравнений.
10. Возрастание средней приспособленности.
11. Мутации
12. Взаимодействие отбора и мутаций.
13. Миграции.
14. Дрейф генов
15. Возбудимые системы.
16. Натриево - калиевый цикл.
17. Аксон Ходжкина - Хаксли.
18. Структура и функции нейронов.
19. Формальный нейрон Мак-Каллока - Питтса.
20. Однослойный персептрон - простейшая модель ассоциативной памяти.
Работа над любой математической моделью начинается со сбора и анализа фактического материала. Определяются цели моделирования. Выделяются главные черты изучаемого объекта или явления. Вводятся формализованные характеристики. Принимаются правила работы с ними. В результате возникает математический объект, который и называется математической моделью. Разрабатываются методы математического анализа модели, которыми она исследуется. Полученные результаты математического моделирования интерпретируются в рамках исходного фактического материала, что позволяет оценить степень адекватности модели. Результаты моделирования не должны противоречить выделенным ранее ключевым экспериментальным фактам. Одновременно, модель не может объяснить все стороны изучаемого объекта или явления.
Хорошая модель, кроме объяснения известных, должна давать возможность предсказывать новые свойства. Математическое моделирование широко используется там, где экспериментальные исследования трудоемки и дорогостоящи, или вообще невозможны (например, в изучении социальных явлений).
Кроме задачи о прогнозе, математическое моделирование помогает классифицировать и систематизировать фактический материал, увидеть существующие связи в мозаике фактов. Это вытекает из того, что модель является специфическим -ярким и выразительным языком, предназначенным для описания для описания изучаемого объекта или явления.
Мир математических моделей разнообразен. Существуют различные схемы их классификации. Однако, каждая модель конкретна и предназначена для описания достаточно узкого круга объектов и явлений. Это накладывает определенный отпечаток на предлагаемый лекционный курс. Он включает в себя модели. относящиеся к различным областям естествознания. Модели сильно отличаются друг от друга не только предметными областями, но математической терминологией, а также математическими методами их исследования.
Предпочтение отдается более простым моделям. Отметим, что "простота" (иногда в ущерб точности)-один из принципов, о котором всегда нужно помнить при разработке математической модели.
Часть1 Основы математической генетики
В 1865 г. чешский монах Грегор Мендель опубликовал работу о результатах скрещивания разновидностей гороха. В своих опытах Г. Мендель изучал закономерности наследования семи пар альтернативных признаков. В одном из опытов перекрестно скрещивались растения с гладкими и сморщенными семенами. В результате такого скрещивания в первом поколении все растения имели гладкие семена. Проявляющиеся признаки Г.Мендель назвал доминантными, а не проявляющиеся - рецессивными. Растениям, полученным в первом поколении, была предоставлена возможность самоопыляться. Во втором поколении появились как гладкие, так и сморщенные горошины. При подсчете выяснилось, что 5 474 горошины были гладкими, а 1 850 - морщинистыми. Доля гладких горошин оказалась близкой к 3/4, а морщинистых - к 1/4. Отношение близко к 3:1. Во всех других опытах для каждой пары альтернативных признаков (например, цвет горошин) доминантный признак обнаруживался примерно втрое чаще рецессивного. Для объяснения результатов опытов Г.Мендель предположил, что внешние признаки определяются некоторыми внутренними факторами (генами), которые могут находиться в одной из двух альтернативных форм (теперь они называются аллелями). Были сделаны два допущения.
1. Два фактора, определяющие данный признак, в течении жизни организма сосуществуют независимо друг от друга, не сливаясь и не растворяясь один в другом. Они расщепляются при формировании половых клеток, которые возникают парами. Одна из половых клеток несет в себе один, а другая - оставшийся фактор.
2. Гены, определяющие различные признаки, наследуются независимо.
Работа Г.Менделя была не понята и забыта его современниками. В 1900 г. результаты были открыты вновь. Началось развитие новой науки -генетики. Согласно современным представлениям, носителями генов являются нитевидные тела -хромосомы, которые располагаются в ядре клетки. Организмы, относящиеся к различным биологическим видам имеют разную структуру и число хромосом. У человека каждая клетка содержит 46 хромосом, у гороха -14. Число хромосом четно. Каждая хромосома в клетке присутствует в двух экземплярах, отличающихся, быть может только аллелями (вариантами, или формами) генов. Такие пары хромосом называются гомологичными. Место, занимаемое аллелью гена в хромосоме, называется локусом. Можно представить хромосому как прямолинейный отрезок, а локусы как его последовательные участки.
Половые клетки -гаметы возникают в результате процесса, который называется мейозом. Гомологичные хромосомы расходятся в разные концы клетки, и клетка делится пополам. Гаметы содержат половинный набор хромосом (у человека 23). Зародышевая клетка -зигота образуется путем слияния мужской и женской гамет и содержит полный набор хромосом. Из зиготы путем обычного деления - митоза образуется новый организм. При митозе каждая хромосома создает свою точную копию. Оригиналы и копии расходятся в разные клетки. Набор генов каждой клетки называется генотипом организма. Описанная схема упрощена. но в ней отражаются ключевые моменты, которые используются при разработке математической модели.
Фенотипом называется совокупность всех внешних признаков организма. Фундаментальный принцип генетики - при неизменных внешних условиях фенотип организма определяется его генотипом. Некоторые признаки организма определяются не всем не всем генотипом, а только его частью (в экспериментах Г.Менделя - двумя аллелями одного гена). Пол человека определяется двумя половыми хромосомами X и Y. Женская зигота содержит две хромосомы X, мужская -хромосомы X и Y.
Мать передает своему ребенку одну из хромосом X. Отец передает дочери хромосому X, а сыну - хромосому Y. Таким образом, пол ребенка зависит только от отца.
Совокупность генотипов, у которых часть генных наборов одинакова, называется популяцией (по данным наборам). Численность популяции считается достаточно большой (бесконечной). Описывать популяцию будем набором частот генотипов в данном поколении. Будем считать, что одно поколение сменяет другое, т.е. поколения не перекрываются.
Законы Менделя
Рассмотрим рассуждения Г.Менделя, используя описанные выше термины. За форму семян гороха отвечает двухаллельный ген. Его доминантную аллель (фенотип -гладкие семена) обозначим как , а рецессивную как a (сморщенные семена). Генотип определяется парой аллелей. Возможны три генотипа: AA, Aa, aa. Генотип Aa называется гетерозиготным, а генотипы AA, aa -гомозиготными. Поскольку аллель A является доминантным, то растения первых двух генотипов будут иметь гладкие семена, а третьего -морщинистые.
На первом этапе своего опыта Г.Мендель брал гомозиготные растения AA, aa. Первый тип давал гамета, имеющие аллель A, второму соответствовали гаметы с аллелью a.
Скрещивание гомозиготных растений AA и aa (слияние гамет A и a) дает гетерозиготное растение Aa. Последнее дает гаметы, несущие аллели A и a. Какую из двух аллелей получит конкретная гамета -дело случая и вероятность каждого из событий 1/2.
На втором этапе опыта Г.Менделя скрещивались гетерозиготные растения. Генотип AA у потомка имеет место, если каждый из родителей передал гамету с аллелем A. События независимые. Вероятность P(AA) потомка с генотипом AA равна 1/4. Аналогично, вероятность P(aa) появления потомка aa также 1/4. Вероятность появления потомка с генотипом Aa можно вычислить по дополнению: P(Aa)=1-1/4-1/4=1/2. Вероятность того, что растение -потомок двух гетерозиготных родителей будет иметь гладкие семена: P(AA)+P(Aa)=1/4+1/2=3/4. Морщинистые семена будут наблюдаться с вероятностью P(aa)=1/4.
Такова математическая модель, объясняющая опыты Г.Менделя. Обсудим вопрос об ее адекватности. Напомним, что в опытах соответствующие частоты наблюдались приближенно. Это задача о проверке статистической гипотезы. Для проверки можно использовать критерий Пирсона.
Предположим, что мы наблюдаем
серию из n независимых испытаний. Каждое из них может завершиться одним из m
исходов  .
Вероятности исходов
.
Вероятности исходов  не меняются от испытания к
испытанию. Подлежащая проверке нуль -гипотеза состоит в том, что эти вероятности
равны некоторым заранее заданным числам:
не меняются от испытания к
испытанию. Подлежащая проверке нуль -гипотеза состоит в том, что эти вероятности
равны некоторым заранее заданным числам:  . Относительно числа n
предполагается. что оно достаточно велико. Пусть
. Относительно числа n
предполагается. что оно достаточно велико. Пусть  -полученные в результате опыта
эмпирические частоты наступления исхода
-полученные в результате опыта
эмпирические частоты наступления исхода  . Составляется сумма:
. Составляется сумма:
 ,
,
которая часто называется суммой
Пирсона. Оказывается, что с ростом n распределение статистики S стремится к
предельному распределению  с m-1 степенями свободы, не
зависящему ни от n, ни от чисел
с m-1 степенями свободы, не
зависящему ни от n, ни от чисел  . Для любого e >0 можно указать практическую границу
. Для любого e >0 можно указать практическую границу  такую, что
такую, что
 .
.
Другими словами, неравенство  >
> практически
невозможно. Число e называется уровнем
значимости.
практически
невозможно. Число e называется уровнем
значимости.
Зададимся уровнем значимости e =0.05, который очень популярен в биологии.
В рассматриваемом случае число степеней свободы m-1=1. Распределение суммы
Пирсона для столь большого числа, как n=7 324 практически не отличается от  распределения
с одной степенью свободы. По таблицам определяем
распределения
с одной степенью свободы. По таблицам определяем  »
3.84. Вычислим сумму Пирсона:
»
3.84. Вычислим сумму Пирсона:

Так как сумма Пирсона меньше  , то нуль-
гипотеза хорошо согласуется с результатами эксперимента. Получаем веские
основания считать, что закон Менделя справедлив.
, то нуль-
гипотеза хорошо согласуется с результатами эксперимента. Получаем веские
основания считать, что закон Менделя справедлив.
В генетике развит некий формализм, позволяющий быстро выводить закономерности. Аллельные пары представляют в виде:
 ,
,  ,
,  ,
,
Скрещивание генотипов обозначается знаком '´ ' -умножения. Скобки в формулах раскрываются по привычным правилам и знаки умножения опускаются. Скрещивание гетерозиготных растений описывается формулой:

Полученная формула утверждает, что генотипы AA и aa возникают при скрещивании с вероятностью 1/4, а генотип Aa с вероятностью 1/2. Так как генотипы AA и Aa обладают гладкими семенами, то 3/4 потомства имеют гладкие семена, а 1/4 - морщинистые семена (генотип aa).
Решим простую задачу о скрещивании генотипов Aa и aa:

Таким образом, половина генотипов будет гетерозиготными, а половина гомозиготными.
Большинство признаков генотипа контролируется более чем двумя аллелями. Такие аллели называются множественными. Такие аллели в любом непарном сочетании могут находиться в любой клетке, так как только две аллели одного гена могут одновременно присутствовать в генотипе. Такие генотипы называются диплоидными. Полиаллельными являются гены, контролирующие группы крови. Группа крови человека зависит от присутствия либо отсутствия в эритроцитах специфических белков (A и B). Существуют четыре группы крови: Группа крови A с генотипами AA и AO (группа крови содержит белок A), группа крови B с генотипами BB и BO (содержит белок B), Группа крови AB (содержит оба белка), группа крови OO (отсутствие белков A и B). Таким образом, группа крови контролируется тремя аллелями A, B, O одного гена. Аллели A и B -доминанты по отношению к O. В присутствия аллелей A и B доминантность отсутствует. Таким образом группы крови определяются шестью генотипами AA, AO, AB, BB, BO, OO.
Закон Харди- Вайнберга
В законе Харди -Вайнберга речь идет о частотах генотипов в популяциях. Этот закон сформулировали в 1908 г. независимо друг от друга английский математик Дж.Харди и австрийский врач В.Вайнберг. Рассматривалась следующая задача. Известны частоты генотипов в двухаллельной популяции в нулевом поколении. Требуется проследить изменение частот от поколения к поколению.
Двухаллельная популяция состоит из генотипов: AA, Aa, aa. Их частоты в нулевом (начальном) поколении обозначим через u(0), 2v(0), w(0). Естественно, что u(0)+2v(0)+w(0)=1. Скрещивание предполагается случайным. Удобно следить за эволюцией частот с помощью следующей схемы.
Нулевое поколение
Генотипы Частоты генотипов
AA u(0)
Aa 2v(0)
aa w(0)
Гаметы Частоты гамет
A; p(0)=u(0)+v(0)
a q(0)= v(0)+w(0)
(менделевское формирование гамет)
Первое поколение
Генотипы Частоты генотипов
AA 

Aa  ;
;
aa 
Гаметы Частоты гамет
A 
a; 
;Таким образом, частоты гамет не меняются от поколения к поколению. Дальнейшее скрещивание не меняет и частоту зигот.
Второе поколение
Генотипы Частоты генотипов
AA 

Aa  ;
;
aa 
Частоты зигот устанавливаются в первом поколении и больше не меняются.
Закон Харди-Вайнберга состоит из следующих двух утверждений.
1. Частоты гамет (аллелей) не меняются от поколения к поколению.
2. Равновесные частоты генотипов достигаются за одно поколение. В популяции поддерживается соотношение между гомозиготными и гетерозиготными организмами:
 .
.
Закон Харди-Вайнберга
распространяется на любое число аллелей  . Очевидно, что число гомозигот
. Очевидно, что число гомозигот  суть m, а
гетерозигот
суть m, а
гетерозигот  . Общее число зигот будет
. Общее число зигот будет  . Рассуждения
для многоаллельного случая полностью аналогичны предыдущему.
. Рассуждения
для многоаллельного случая полностью аналогичны предыдущему.
Нулевое поколение
Генотипы Частоты генотипов




Гаметы Частоты гамет


Первое поколение
Генотипы Частоты генотипов





Гаметы Частоты гамет


Таким образом, частоты гамет не меняются от поколения к поколению. Дальнейшее скрещивание не меняет и частоту зигот.
Второе поколение
Генотипы Частоты генотипов




Для всех последующих поколений
частоты генотипов остаются такими же:  ,
,  . Это и есть закон Харди -Вайнберга
для полиаллельного локуса.
. Это и есть закон Харди -Вайнберга
для полиаллельного локуса.
Обсудим некоторые аспекты закона Харди -Вайнберга. В случае доминирования аллеля A над a наблюдаются лишь фенотипы {AA, Aa}, {a,a}. В силу закона Харди -Вайнберга их вероятности равны

где  -частота рецессивного аллеля a.
-частота рецессивного аллеля a.
Если рецессивный аллель -редкий
( ), то
соответствующий фенотип наблюдается еще реже. Частота наблюдения альбиносов
(генотип aa, он же - фенотип)
), то
соответствующий фенотип наблюдается еще реже. Частота наблюдения альбиносов
(генотип aa, он же - фенотип)  . Это - экспериментальный факт. В
силу закона Харди -Вайнберга, скрытые носители рецессивного аллеля (генотип Aa)
встречаются гораздо чаще:
. Это - экспериментальный факт. В
силу закона Харди -Вайнберга, скрытые носители рецессивного аллеля (генотип Aa)
встречаются гораздо чаще:
 .
.
Если доминантный аллель
является редким:  , то частота его проявления
примерно вдвое больше:
, то частота его проявления
примерно вдвое больше:
 .
.
Интересная ситуация складывается сейчас в человеческой популяции. Существуют рецессивные летальные аллели (генотип aa нежизнеспособен). Примером может служить наследственная болезнь фенилкотонурия (ФКУ). Сейчас найдены способы ее лечения. Выздоровевшие люди могут давать потомство и передавать ему аллель ФКУ. Тем самым частота летальных генов будет возрастать.
Сделаем некоторые замечания о
математических аспектах закона Харди -Вайнберга. Обозначим частоты генотипов AA,
Aa, aa через  . Здесь
. Здесь  и
и
 .
.
Эти соотношения выделяют в
трехмерном пространстве треугольник. В следующем поколении частоты  выражаются
через частоты
выражаются
через частоты  по формулам:
по формулам:

 (1)
(1)

Формулы задают отображение треугольника в себя, которое назовем оператором эволюции и обозначим через V. Закон Харди -Вайнберга означает, что
 . (2)
. (2)
Эта формула отражает принцип стационарности, который С.Н. Бернштейн возвел в ранг закона.
Основная проблема, которой
занимался С.Н. Бернштейн, - выявление всех законов наследования, подчиненных
закону стационарности. Он дал ее полное решение для популяций, состоящих из
трех генотипов, а также изучил некоторые случаи большего числа генотипов. Среди
них пример популяции с m -аллельным геном. Пусть его аллели  . Генотипы
популяции:
. Генотипы
популяции:  ,
при этом
,
при этом  .
Обозначим частоты генотипов в текущем поколении через
.
Обозначим частоты генотипов в текущем поколении через  . Неотрицательные числа
. Неотрицательные числа  очевидно удовлетворяют
соотношению:
очевидно удовлетворяют
соотношению:
 .
.
Пусть  частоты генотипов в
следующем поколении. Оператор эволюции имеет следующий вид:
частоты генотипов в
следующем поколении. Оператор эволюции имеет следующий вид:

 .
.
Из закона Харди -Вайнберга для полиаллельных популяций следует, что для данного эволюционного оператора также выполнен принцип стационарности (2).
В одной из работ С.Н.
Бернштейна рассматривался так называемый кадрильный закон наследования,
генетическая интерпретация которого принадлежит Ю.И. Любичу. Введем два вида
"женских " X, x и два вида "мужских" ген Y, y.
Будем считать, что могут существовать лишь четыре генотипа: XY, xy, Xy, xY,
которым присвоим номера 1, 2, 3, 4. Остальные мыслимые комбинации генов
запретим. Частоты генотипов в нулевом поколении обозначим через  , а в следующем -через
, а в следующем -через  . Поскольку
при образовании зиготы объединяется одна женская и одна мужская гаметы, то
следует говорить о частотах гамет X и x среди женских и о
частотах гамет Y и y среди мужских. Частоты женских гамет в
нулевом поколении:
. Поскольку
при образовании зиготы объединяется одна женская и одна мужская гаметы, то
следует говорить о частотах гамет X и x среди женских и о
частотах гамет Y и y среди мужских. Частоты женских гамет в
нулевом поколении:
 ,
, 
 .
.
Частоты мужских гамет:


 .
.
Частоты генотипов в первом поколении:



 .
.
Отсюда получаем:




Данное отображение и изучал С.Н. Бернштейн. Частоты генов в первом поколении

(аналогично для других частот), т.е. сохраняются.
С.Н. Бернштейн показал
неизбежность концепции гена в условиях Менделя. Сформулируем этот результат.
Обозначим через  вероятность появления потомка
вероятность появления потомка  у родителей
у родителей  и
и  . Генотип
. Генотип  называется
исчезающим, если появление потомка
называется
исчезающим, если появление потомка  у любой пары родителей равно нулю.
у любой пары родителей равно нулю.
Теорема. Если в трехмерной популяции

все генотипы не исчезающие и  , (при
скрещивании первого со вторым получается только третий), то популяция
менделевская.
, (при
скрещивании первого со вторым получается только третий), то популяция
менделевская.
Вернемся еще раз к вопросу о группах крови. В 1925 г. Ф. Бернштейн выдвинул гипотезу, что группа крови определяется тремя аллелями A, B, O одного локуса с доминированием A и B над O (в случае присутствия A и B доминантность отсутствует). Фенотипы: {AB}, {AO, AA}, {BO, BB}, {OO}. Согласно закону Харди -Вайнберга для одного трехаллельного локуса имеем:




откуда вытекает соотношение:


Для населения Японии известны
следующие статистические данные: 


 . Экспериментальное значение величины
. Экспериментальное значение величины
 , что
хорошо согласуется со статистическим прогнозом. Данное обстоятельство можно
интерпретировать в пользу гипотезы.
, что
хорошо согласуется со статистическим прогнозом. Данное обстоятельство можно
интерпретировать в пользу гипотезы.
Инбридинг
Закон Харди -Вайнберга действует только тогда, когда скрещивание случайно, т.е. вероятность скрещивания между двумя генотипами равна произведению их частот. В тех случаях, когда скрещивание неслучайно, имеет место ассортивное, или предпочтительное скрещивание. Особи с определенными генотипами скрещиваются чаще, чем следует ожидать на основе случайности. Ассортивное скрещивание не меняет частот генов, но изменяет частоты генотипов.
Особенно интересную форму ассортивного скрещивания представляет собой инбридинг, при котором скрещивание между родственными особями происходит чаще, чем этого можно было бы ожидать на основе случайности. Инбридинг ведет к повышению частот гомозигот и уменьшает частоту гетерозигот по сравнению с ожидаемыми при случайном скрещивании. Самым крайним случаем инбридинга является самоопыление -форма размножения, широко распространенная для некоторых групп растений.
Мерой генетических последствий
инбридинга служит коэффициент инбридинга. Это вероятность того, что особь
является гомозиготной и оба (одинаковых) аллеля идентичны по происхождению,
т.е. унаследованы у одного и того прародителя из некоторого предшествующего
поколения. Отметим, что два одинаковых аллеля могут быть наследованы от разных
предков. Коэффициент инбридинга обозначим через  .
.
Результаты инбридига в случае
самоопыления анализировались еще Г. Менделем. Он исследовал потомство
гетерозиготных растений (генотип Aa) после n поколений
самоопыления. В первом поколении частоты гомозиготных растений: 
 Ясно, что гомозиготные
растения идентичны по происхождению. Гетерозиготные растения не идентичны по
происхождению и их частота
Ясно, что гомозиготные
растения идентичны по происхождению. Гетерозиготные растения не идентичны по
происхождению и их частота  Здесь и ниже нижний индекс -номер
поколения. Коэффициент инбридинга -частота гомозиготных растений, т.е.
Здесь и ниже нижний индекс -номер
поколения. Коэффициент инбридинга -частота гомозиготных растений, т.е.  .
.
Во втором поколении потомки
гомозиготных растений также гомозиготны и идентичны по происхождению. Частоты
гомозиготных растений увеличиваются дополнительно за счет потомков
гетерозиготных растений: 

Частота гетерозиготных растений
во втором поколении:  Коэффициент инбридинга
Коэффициент инбридинга  .
.
Для произвольного n -ого
поколения при самоопылении растений частота гетерозиготных растений 
Если учесть, что  и
и  то в n
-ом поколении частоты гомозиготных растений суть
то в n
-ом поколении частоты гомозиготных растений суть


Коэффициент инбридинга
соответственно 
Он монотонно возрастает с
ростом номера поколения Для самоопыляющихся растений с ростом номера поколения,
снижается доля гетерозиготных и растут частоты гомозиготных растений. В каждом
поколении коэффициент инбридинга в потомстве гетерозиготных растений один
и тот же и равен  . В пределе гетерозиготные растения
вообще исчезают. Этот результат и был получен Г.Менделем.
. В пределе гетерозиготные растения
вообще исчезают. Этот результат и был получен Г.Менделем.
Определим значение коэффициента инбридинга в потомстве сибсов, т.е, особей имеющих общую пару родителей. Родословная потомства от скрещивания сибсов изображена на диаграмме.

Пусть A и B -не
состоящие в родстве родители, из гамет которых образуются зиготы C и D.
Зигота E возникает от слияния гамет от C и D, т.е. от
сибсов. Поскольку A и B не состояли в родстве, что их аллели в
рассматриваемом локусе не идентичны по происхождению. Эти аллели для особи A
обозначим как  , а для особи B - как
, а для особи B - как  (аллели не
идентичны по происхождению, но могут быть идентичны по структуре). Нужно
определить вероятность появления в потомстве сибсов гомозиготной особи. Она
может принадлежать одному из четырех генотипов: или
(аллели не
идентичны по происхождению, но могут быть идентичны по структуре). Нужно
определить вероятность появления в потомстве сибсов гомозиготной особи. Она
может принадлежать одному из четырех генотипов: или  , или
, или  , или
, или  , или
, или  . Вероятность того, что родитель A
передаст аллель
. Вероятность того, что родитель A
передаст аллель  сибсу C суть
сибсу C суть  . В свою очередь, если
особь C получила аллель
. В свою очередь, если
особь C получила аллель  , то она передаст ее особи E так
же с вероятностью
, то она передаст ее особи E так
же с вероятностью  . В итоге особь E получит
аллель
. В итоге особь E получит
аллель  от
A через C с вероятностью
от
A через C с вероятностью  . Вторую алелль
. Вторую алелль  особь E от A
через D приобретет также с вероятность
особь E от A
через D приобретет также с вероятность  . Вероятность того, что
интересующая нас особь E гомозиготна и принадлежит генотипу
. Вероятность того, что
интересующая нас особь E гомозиготна и принадлежит генотипу  есть
есть  . Совершенно
аналогичные рассуждения позволяют определить для особи E вероятности
. Совершенно
аналогичные рассуждения позволяют определить для особи E вероятности  ,
,  ,
,  принадлежать
соответствующему генотипу. Получаем коэффициент инбридинга
принадлежать
соответствующему генотипу. Получаем коэффициент инбридинга  , совпадающий с
вероятностью того, что особь E гомозиготна и получила оба аллеля либо от
прородителя A, либо B.
, совпадающий с
вероятностью того, что особь E гомозиготна и получила оба аллеля либо от
прородителя A, либо B.
Существует простой метод, так
называемый анализ путей, позволяющий определить коэффициент инбридинга
для любого организма с известной родословной. На диаграмме, отражающей
родословную рассматриваются все замкнутые пути, включающие в себя изучаемую
особь, ее родителей и их общих предков. Для каждого i -ого цикла определяется
коэффициент  , где
, где  -число звеньев в цикле. Коэффициент
инбридинга
-число звеньев в цикле. Коэффициент
инбридинга  .
.


Поясним сказанное, вычислив коэффициент инбридинга для особи K, родословная которой изображена на диаграмме.

Согласно диаграмме A и B
общие предки для родителей J и H особи K. Имеются два
замкнутых пути K -J -G -C -A -D -H -K и K -J -G -C -B -D -H -K,
каждый из которых состоит из 7 звеньев. Соответственно  и
и  . Коэффициент инбридинга
. Коэффициент инбридинга
 .
.
Напомним, что в результате
инбридинга частоты гомозигот в популяции возрастают за счет гомозигот. В
популяции с постоянным (не растущим) коэффициентом инбридинга  частота гомозигот будет
составлять
частота гомозигот будет
составлять 
 от частоты в
случайно скрещивающейся популяции. Пусть частоты аллелей A и a
суть p и q. Частоты генотипов в инбредной популяции с
постоянным коффициентом инбридинга можно представить следующим образом:
от частоты в
случайно скрещивающейся популяции. Пусть частоты аллелей A и a
суть p и q. Частоты генотипов в инбредной популяции с
постоянным коффициентом инбридинга можно представить следующим образом:
Генотип Частота
AA  ,
,
Aa  ,
,
aa  .
.
Частоты аллелей, а вместе с
ними и генотипов сохраняются при переходе от поколения к поколению. При
отсутствии имбридинга  частоты удовлетворяют закону Харди
-Вайнберга.
частоты удовлетворяют закону Харди
-Вайнберга.
Селекционеры стремятся вывести сорта растений и породы животных, отличающиеся максимальными показателями хозяйственно полезных признаков. При этом в качестве родителей используют наилучшие организмы, т.е. проводят искусственных отбор. Селекционеры также стараются получить как можно более однородные сорта и породы. Для этого применяют систематический инбридинг, повышающий гомозиготность. Однако, хорошо известно, что инбридинг обычно понижает приспособленность потомства. Это явление принято называть инбредной депрессией. Оно обусловлено повышением степени гомозиготности по вредным рецессивным аллелям.
Инбредной депрессии противопоставляют скрещивание между представителями независимых инбредных линий. Гибриды обычно обнаруживают заметно возросшую приспособленность - в плодовитости, жизнеспособности и т.д. При скрещивании между двумя инбредными линиями можно сохранить в потомстве гомозиготность по искусственно отобранным признакам, тогда как по вредным аллелям особи являются гетерозиготными.
Сцепление и кроссиговер
Г.Мендель наблюдал независимое наследование семе признаков. Это происходило потому, что все семь соответствующих генов расположены в локусах разных негомологиных хромосом. Напомним, что у гороха в каждой клетке находится семь пар гологичных хромосом. Наблюдать независимое наследование дополнительно еще одного признака в принципе невозможно. Гены, расположенные в одной хромосоме, называются сцепленными. Рассмотрим два локуса, одной и той же хромосоме (такие же локусы присутствуют в гомологичной хромосоме). Обозначим аллели гена первого локуса через A и a, а другого -как B и b. В отличие от однолокусного случая, гаметы будем обозначать словами. Таких слов - четере: AB, Ab, aB, ab. Если бы каждая хромосома была неразрывным целым, то мысленно можно было бы объдинить два локуса в один и рассматривать однолокусную четерехаллельную популяцию. Законы наследования в такой популяции изучались выше. Однако, предсказания такой теории вступают в сильные противоречия с некоторыми экспериментальными данными.
Известнейший генетик Томас Морган проводил эксперименты с мухами - дрозофилами. Отслеживались два признака: окраска тела и длина крыльев. В результате экпериментов по скрещиванию сразу же была опровергнута гипотеза, что соответствующие локусы находятся в разных хромосомах (в этом случае признаки должны были бы наследоваться независимо, что не соответствует реальности). Пусть за окраску тела отвечает первый локус. Его аллели: A (доминантный) - коричневая окраска, a (рецессивный) -черная окраска. Длина крыльев определяется вторым локусом. Доминантный аллель B соответствует длинным крыльям, а рецессивный аллель b - коротким. При интерпретации опытов постараемся опираться на однолокусовую черырехаллельную модель. На первом этапе Т.Морган скрещивал черных длиннокрылых самок и коричневых самцов с короткими крыльями. Генотип самок -(aB)(aB), генотип самцов (Ab)(Ab). Результат скрещивания:

Особи этого генотипа имеют коричневую окраску и длинные крылья. На данном этапе предсказания теории полностью соответствовали результатам опыта. На втором этапе полученных самок Т.Морган скрещивал с черными самцами, имеющими короткие крылья. Они принадлежали генотипу (aa)(bb). Попытаемся предсказать результат скрещивания:

Таким образом, в результате
описанной стратегии срещивания дожны появляться с вероятностью  особи двух генотипов (aB)(ab)
и (Ab)(ab). Первые имеют черную окраску и длинные крылья, а вторые
коричневую окраску и короткие крылья. Результат опыта оказался в противоречии с
предсказаниями теории: появились мухи коричневые с длинными крыльями (8.5%) и
черные мухи с короткими крыльями (8.5%). На 8.5% по сравнению с теорией
уменьшилось число особей каждого из первых двух генотипов.
особи двух генотипов (aB)(ab)
и (Ab)(ab). Первые имеют черную окраску и длинные крылья, а вторые
коричневую окраску и короткие крылья. Результат опыта оказался в противоречии с
предсказаниями теории: появились мухи коричневые с длинными крыльями (8.5%) и
черные мухи с короткими крыльями (8.5%). На 8.5% по сравнению с теорией
уменьшилось число особей каждого из первых двух генотипов.
Была высказана гипотеза (она подтверждена), что в процессе мейоза (образавания половых клеток) гамологичные хромосомы могут обмениваться своими частями. Такой обмен аллелями между гомологичными хромосомами называется кросинговером. Его иллюстрирует рисунок.

Обратим внимание на важное обтоятельство, которое легко понять, глядя на рисунок. Пусть в одном из локусов обеих гомологичных хромосом находится один и тот же аллель. Тогда кроссигговер, даже если он произошел, не меняет локусные пары.
Благодаря кроссинговеру сцепленные гены могут передаваться потомству в сочетаниях, отличных от тех, которые были у родителей. В частности на рисунке родительская особь генотипа (AB)(ab) в результате кроссинговера породила гаметы (Ab) и (aB). Без кроссинговера мейоз привел бы к появлению гамет (AB) и (ab).
Обратимся к уравнениям,
описывающим эволюцию в популяции с двумя двухаллельными локусами при условии
кроссинговера. Частоты гамет в текущям и последующем поколениях будем
обозначать как  и
и  . Так, например,
. Так, например,  -частота гамет, у
которых в первом локусе находится аллель A, а во втором - аллель b.
Частоты генотипов в текущем поколении связаны с частотами гамет этого же
поколения (до мейоза). Приведем примеры. Частота гомозиготного генотипа (AB)(AB)
суть
-частота гамет, у
которых в первом локусе находится аллель A, а во втором - аллель b.
Частоты генотипов в текущем поколении связаны с частотами гамет этого же
поколения (до мейоза). Приведем примеры. Частота гомозиготного генотипа (AB)(AB)
суть  , а
частота гетерозиготного генотипа (AB)(ab) - соответственно
, а
частота гетерозиготного генотипа (AB)(ab) - соответственно  . Эти и все
подобные формулы полностью соответствуют случаю одного полиаллельного локуса.
Обозначим через m и l вероятности того, что при мейозе
соответственно произошел или не произошел кроссинговер. Здесь, естественно, m +l
=1. Выпишем уравнения для эволюции частот гамет:
. Эти и все
подобные формулы полностью соответствуют случаю одного полиаллельного локуса.
Обозначим через m и l вероятности того, что при мейозе
соответственно произошел или не произошел кроссинговер. Здесь, естественно, m +l
=1. Выпишем уравнения для эволюции частот гамет:


(3)


Дадим комментарии к правой
части первой формулы (остальные формулы выписываются аналогично). Первое слагаемое
- частота генотипа (AB)(AB). При мейозе каждая особь данного
генотипа с единичной вероятность порождает гаметы (AB). Второе слагаемое
- половинная частота генотипа (AB)(Ab). В силу сделанного выше
замечания, несмотря на кроссиговер, каждая особь этого генотипа с вероятностью  при мейозе
дает гаметы (AB) и (Ab) (нас в данном случае интересуют гаметы (AB)).
Совершенно аналогично, отражает вклад генотипа (AB)(aB) в образование
гамет (AB). Четвертое слагаемое выписывается из следующих соображений.
При условии, что кроссинговер не произошел (вероятность l ), особь генотипа (AB)(ab) с вероятностью
при мейозе
дает гаметы (AB) и (Ab) (нас в данном случае интересуют гаметы (AB)).
Совершенно аналогично, отражает вклад генотипа (AB)(aB) в образование
гамет (AB). Четвертое слагаемое выписывается из следующих соображений.
При условии, что кроссинговер не произошел (вероятность l ), особь генотипа (AB)(ab) с вероятностью  даст гамету (AB).
Частота генотипа (AB)(ab) суть
даст гамету (AB).
Частота генотипа (AB)(ab) суть  . Обратимся к последнему
слагаемому. При условии кроссинговера (вероятность m ) особь генотипа (Ab)(aB) (частота
. Обратимся к последнему
слагаемому. При условии кроссинговера (вероятность m ) особь генотипа (Ab)(aB) (частота  ) с
вероятностью
) с
вероятностью  порождает гамету (AB) (см.
рисунок выше). Осталось заметить, что кроссинговер ни в каком другом генотипе
не может привести к появлению гаметы (AB).
порождает гамету (AB) (см.
рисунок выше). Осталось заметить, что кроссинговер ни в каком другом генотипе
не может привести к появлению гаметы (AB).
Преобразуем формулы (3).
Выкладки проведем на примере первой формулы. Подставляя  , получим
, получим

Здесь учтено, что  .
.
Введем обозначение 
В результаты преобразований формулы (3) приобретают вид:

 (4)
(4)


Величина  называется мерой
неравновесности состояния (если
называется мерой
неравновесности состояния (если  , то частоты гамет постоянны).
Рассмотрим эволюцию
, то частоты гамет постоянны).
Рассмотрим эволюцию  . В силу (4) имеем:
. В силу (4) имеем:

Итак
 . (5)
. (5)
Проследим за эволюцией частот  ,
,  ,
,  ,
,  (нижний индекс
- номер поколения). В силу (4) и(5)
(нижний индекс
- номер поколения). В силу (4) и(5)
 (6)
(6)
 .
.
Это система так называемых разностных уравнений. Она решается следующим образом. Выписывается матрица правых частей уравнений:
 .
.
Находятся ее собственные
значения  и
и
 . Матрица
. Матрица
 -
диагональная, поэтому
-
диагональная, поэтому  ,
,  . Собственные векторы
. Собственные векторы  (нетривиальные
решения систем
(нетривиальные
решения систем  ) суть
) суть
 ,
,  .
.
При вычислении  использовано равенство:
использовано равенство:  . Система
резностных уравнений (6) имеет два линейно независимые решения:
. Система
резностных уравнений (6) имеет два линейно независимые решения:  и
и  . Общим решением
является их линейная комбинация:
. Общим решением
является их линейная комбинация:
 .
.
Константы  и
и  определяются из
начального условия (при
определяются из
начального условия (при  ):
):
 .
.
Получаем  и
и  . В результате получаем
решение системы (6):
. В результате получаем
решение системы (6):
 ,
,
 .
.
Совершенно аналогично исследуется изменение частот гамет (ab), (Ab), (aB):
 ,
,
 ,
,
 .
.
Из полученных формул следует,
что при  (с
ростом номера поколения)
(с
ростом номера поколения)  и
и
 ,
, ,
,  ,
,  .
.
Тем самым, частоты гамет стремятся к состоянию равновесия, которое не достижимо за конечное число поколений. Частоты генотипов определяются через частоты гамет, а, следовательно, также стабилизируются. В отличии от случая, соответствующего закону Харди -Вайнберга, стабилизация в первом поколении не наступает.
Как уже говорилось, начальное
состояние равновесно, т.е. частоты гамет в дальнейшем не меняются, если  , т.е.
, т.е.
 .
.
Исследуем условия равновесности. Рассмотрим частоты генов
 ,
,  ,
,
 ,
,  .
.
Легко видеть, что  ,
,  . Прямые
вычисления показывают:
. Прямые
вычисления показывают:



Таким образом,  . Совершенно аналогично:
. Совершенно аналогично:
 ,
,  ,
,  .
.
В равновесных состояниях частоты гамет являются произведениями частот соответствующих генов. Верно и обратное утверждение.
Формальный нейрон Мак-Каллока - Питтса
Модель отражает единственный
атрибут биологического нейрона -его способность генерировать импульсы “все, или
нечего” в ответ на достаточно сильное воздействие. Нейрон Мак-Каллока - Питтса
функционирует в дискретном времени. Он имеет  входов -синапсов и единственный
выход. Значение выходного сигнала
входов -синапсов и единственный
выход. Значение выходного сигнала  соответствует генерации спайка
(состояние возбуждения). В состоянии покоя выходной сигнал
соответствует генерации спайка
(состояние возбуждения). В состоянии покоя выходной сигнал  . В момент времени
. В момент времени  выходной
сигнал формируется в зависимости от сигналов
выходной
сигнал формируется в зависимости от сигналов  , поступивших на синапсы в момент
времени
, поступивших на синапсы в момент
времени  .
Последние также могут принимать значения ноль или единица. Если синаптический
сигнал равен нулю, то говорят, что синапс находится в состоянии покоя.
Единичное значение соответствует состоянию возбуждения синапса. Сигнал на
синапс поступает либо от выхода другого нейроны, либо от сенсора -специального
входа для внешних сигналов. Первоначально правила формирования выходного
сигнала были введены авторами модели в виде ряда аксиом. Приведем две из них.
.
Последние также могут принимать значения ноль или единица. Если синаптический
сигнал равен нулю, то говорят, что синапс находится в состоянии покоя.
Единичное значение соответствует состоянию возбуждения синапса. Сигнал на
синапс поступает либо от выхода другого нейроны, либо от сенсора -специального
входа для внешних сигналов. Первоначально правила формирования выходного
сигнала были введены авторами модели в виде ряда аксиом. Приведем две из них.
1.
Для возбуждения нейрона в момент времени  необходимо в момент времени
необходимо в момент времени  возбудить
определенное, фиксированное число синапсов, которое не зависит ни от предыдущей
истории, ни от состояния нейрона.
возбудить
определенное, фиксированное число синапсов, которое не зависит ни от предыдущей
истории, ни от состояния нейрона.
2.
Нейрон имеет особые входы -тормозящие синапсы. Возбуждение любого из них
в момент времени  исключает возбуждение нейрона в
момент времени
исключает возбуждение нейрона в
момент времени 
Первая аксиома отражает пороговые свойства нейрона, а вторая - подчеркивает особую роль торможения (на сетях “без запретов” нельзя реализовать произвольный алгоритм).
Впоследствии модель изменилась.
Синаптические сигналы  ( не обязательно бинарные) стали
взвешивать и формировать суммарный входной сигнал
( не обязательно бинарные) стали
взвешивать и формировать суммарный входной сигнал  . Здесь
. Здесь  -числа, которые называют
синаптическими весами. Синапс называют возбудительным, если
-числа, которые называют
синаптическими весами. Синапс называют возбудительным, если  , и тормозным, если
, и тормозным, если  .
Договорились, что в момент времени
.
Договорились, что в момент времени  нейрон находится в возбужденном
состоянии
нейрон находится в возбужденном
состоянии  ,
если суммарный входной сигнал в момент времени
,
если суммарный входной сигнал в момент времени  превысил некоторое пороговое
значение
превысил некоторое пороговое
значение  ,
т.е.
,
т.е.  .
Пусть
.
Пусть  -функция
Хевисайта. Она принимает нулевое значение при
-функция
Хевисайта. Она принимает нулевое значение при  и единичное при
и единичное при  . Тогда можно записать:
. Тогда можно записать:
 . (12)
. (12)
Описанный объект есть то, что в настоящее время называют формальным нейроном Мак-Каллока - Питтса.
Функция  в (12) получила название
функции активации. Часто рассматривают нейроны с другими функциями активации.
Нулевое значение выходного сигнала означает, что в соответствующий момент
времени нейрон не действует на другие нейроны (он как бы искючен из сети).
Представляется разумным, что в любой момент времени
в (12) получила название
функции активации. Часто рассматривают нейроны с другими функциями активации.
Нулевое значение выходного сигнала означает, что в соответствующий момент
времени нейрон не действует на другие нейроны (он как бы искючен из сети).
Представляется разумным, что в любой момент времени  выходное значение не равно нулю и
зависит от величины
выходное значение не равно нулю и
зависит от величины  . В связи с этим, часто берут в
качестве функции активации знак числа. Формула для выходного сигнала
приобретает вид:
. В связи с этим, часто берут в
качестве функции активации знак числа. Формула для выходного сигнала
приобретает вид:
 . (13)
. (13)
Здесь  при
при  и
и  при
при  . Отметим, что в данном
случае поделить нейроны на возбудительные и тормозные в принципе невозможно
(напомним, что для биологических нейронов такая классификация производится).
. Отметим, что в данном
случае поделить нейроны на возбудительные и тормозные в принципе невозможно
(напомним, что для биологических нейронов такая классификация производится).
Еще один подход к выбору функции активации связан с биологическим фактом, что на более сильное воздействие нейрон отвечает пачкой спайков. Число спайков (или частоту их следования) можно принять за характеристику выходного сигнала. В связи с этим рассматривают нейрон, у которого выходной сигнал задается формулой:
 . (14)
. (14)
Здесь  -монотонно растущая
функция, имеющая предел
-монотонно растущая
функция, имеющая предел  при
при  . Дополнительно предполагают, что
. Дополнительно предполагают, что  при
при  , либо
, либо  при
при  (сигмоидная
функция). Широко используется так называемая логистическая функция:
(сигмоидная
функция). Широко используется так называемая логистическая функция:  . Другой
вариант:
. Другой
вариант:  при
при
 ,
например,
,
например,  .
.
Иногда в качестве функции  выбирают
линейный трехзвенный сплайн (ломаную, состоящую из трех частей):
выбирают
линейный трехзвенный сплайн (ломаную, состоящую из трех частей):  при
при  ,
,  , где
, где  и
и  ,
,  для
для  . Тогда на
восходящем участке функции активации нейрон работает как линейный сумматор
входных сигналов.
. Тогда на
восходящем участке функции активации нейрон работает как линейный сумматор
входных сигналов.
Рассмотрим нейрон Мак-Каллока -
Питтса, выходной сигнал которого задается формулой (12). Вектор  , состоящий из входных
сигналов (не обязательно бинарных), назовем входным, а вектор
, состоящий из входных
сигналов (не обязательно бинарных), назовем входным, а вектор  -синаптическим. Обычным
образом введем скалярное произведение:
-синаптическим. Обычным
образом введем скалярное произведение:  . Гиперплоскость
. Гиперплоскость  разбивает пространство
разбивает пространство  на два
полупространства
на два
полупространства  и
и  . В первом из них
. В первом из них  , а во втором
, а во втором  . Если входной
вектор
. Если входной
вектор  ,
то выходной сигнал нейрона
,
то выходной сигнал нейрона  , если же
, если же  , то
, то  . Тем самым, нейрон
относит каждый из входных векторов к одному из двух классов.
. Тем самым, нейрон
относит каждый из входных векторов к одному из двух классов.
Для того, чтобы нейрон мог
осуществлять “правильную” в каком -то смысле классификацию, должны быть
соответствующим образом выбраны вектор синаптических весов  и пороговое значение
и пороговое значение  . Процедура
выбора этих параметров называется обучением нейрона. Различают обучение с
“учителем” и “без учителя”.
. Процедура
выбора этих параметров называется обучением нейрона. Различают обучение с
“учителем” и “без учителя”.
Задача обучения с учителем
ставится следующим образом. Задаются два набора входных векторов  и
и  . Они
называются эталонными векторами или паттернами, а также образами. Требуется
определить вектор
. Они
называются эталонными векторами или паттернами, а также образами. Требуется
определить вектор  синаптических весов и порог
синаптических весов и порог  так, чтобы
выходной сигнал нейрона в ответ на входные векторы
так, чтобы
выходной сигнал нейрона в ответ на входные векторы был равен единице, а на векторы
был равен единице, а на векторы  -нулю. Тем
самым, обучение с учителем предполагает, что для каждого эталонного входного
вектора заведомо известен ответ нейрона. Эталон и желаемый ответ называются
обучающей парой.
-нулю. Тем
самым, обучение с учителем предполагает, что для каждого эталонного входного
вектора заведомо известен ответ нейрона. Эталон и желаемый ответ называются
обучающей парой.
Несмотря на многочисленные прикладные достижения обучение с учителем критикуется за свою биологическую неправдоподобность, поскольку совершенно не понятно откуда могут появиться желаемые ответы. При обучении без учителя заранее неизвестно разбиение эталонов на подмножества. До обучения невозможно предсказать в какой класс попадет каждый конкретный эталонный вектор. В процессе обучения выделяются статистические свойства обучающей последовательности и вырабатываются правила классификации. Естественно идея, на которой основаны правила, априорно заложена в процесс обучения. Например, эталонные векторы усредняются по координатам. Если эталонный вектор находится от усредненного “не слишком далеко”, то он относится к первому классу, а иначе -ко второму. Постановка задачи об обучении без учителя выглядит несколько расплывчатой. Однако в ряде случаев она успешно решена.
Различают также внешнее и адаптивное обучение. В первом случае синаптические веса вычисляются неким внешним устройством, а затем импортируются в синапсы. При адаптивном обучении веса подстраиваются в процессе функционирования сети, которой предъявляется обучающая последовательность эталонов. Многие авторы считают механизм адаптации неотъемлемым атрибутом нейронов. Внешнее обучение позволяет понять, во -первых, возможна ли вообще интересующая нас классификация для данной обучающей последовательности. Во -вторых, позволяет, не задумываясь о возможных механизмах адаптации, разумно выбрать синаптические веса для изучения вопроса о функционировании нейронов, объединенных в сеть.
После завершения процесса обучения нейрон осуществляет классификацию векторов эталонной последовательности, т.е. “запоминает” для каждого вектора класс, к которому тот относится. Кроме этого, произвольный входной вектор нейрон относит к определенному классу, т.е. “обобщает” классификацию (принцип сортировки) эталонной последовательности на произвольный образ.
Рассмотрим вопрос о
разрешимости задачи обучения с учителем в частном случае, когда второе
множество состоит из единственного представителя  . Геометрически это означает, что
строится гиперплоскость, которая отделяет векторы
. Геометрически это означает, что
строится гиперплоскость, которая отделяет векторы  от нуля, т.е. решается задача об
отделимости. Отметим, что для бинарных векторов, координаты которых равны либо
нулю, либо единице, задача об отделимости всегда разрешима. В качестве
нормального вектора можно взять, например вектор
от нуля, т.е. решается задача об
отделимости. Отметим, что для бинарных векторов, координаты которых равны либо
нулю, либо единице, задача об отделимости всегда разрешима. В качестве
нормального вектора можно взять, например вектор  и положить для порогового значения
и положить для порогового значения  .
Нижеследующие построения на используют предположения о бинарности векторов.
.
Нижеследующие построения на используют предположения о бинарности векторов.
Легко понять, что задача об
отделимости разрешима в том и только том случае, когда выпуклая оболочка
векторов  не
содержит нуля (отделена от нуля). Напомним, что выпуклой оболочкой векторов
не
содержит нуля (отделена от нуля). Напомним, что выпуклой оболочкой векторов  называется
множество
называется
множество  ,
состоящее из векторов:
,
состоящее из векторов:  , где
, где  и
и  . Пусть множество
. Пусть множество  отделено от нуля и
отделено от нуля и  -его ближайшая
к нулю точка, т.е.
-его ближайшая
к нулю точка, т.е.  по всем
по всем  . Здесь, как обычно,
. Здесь, как обычно,  . Положим
. Положим  и выберем
произвольно
и выберем
произвольно  . Вектор
. Вектор  -искомый синаптический вектор, а
-искомый синаптический вектор, а  -пороговое
значение для нейрона, реагирующего на входные векторы
-пороговое
значение для нейрона, реагирующего на входные векторы  выходным сигналом
выходным сигналом  , а на вектор
, а на вектор  -сигналом
-сигналом  .
.
Задача о нахождении вектора, на
котором реализуется минимальное расстояние от нуля до выпуклой оболочки сама по
себе весьма сложна. Если число векторов  не превышает размерность
пространства и сами они линейно независимы, то отделяющую гиперплоскость можно
построить другим способом. Достаточно провести через векторы
не превышает размерность
пространства и сами они линейно независимы, то отделяющую гиперплоскость можно
построить другим способом. Достаточно провести через векторы  какую-нибудь не
содержащую ноль гиперплоскость, а затем сдвинуть ее по направлению нормали ближе
к нулю. В качестве вектора синаптических весов следует взять нормальный к
какую-нибудь не
содержащую ноль гиперплоскость, а затем сдвинуть ее по направлению нормали ближе
к нулю. В качестве вектора синаптических весов следует взять нормальный к
гиперплоскости вектор,
направленный в полупространство, не содержащее ноль.;Нормальный вектор к
гиперплоскости, содержащей векторы  строится конструктивно. Выбор
вектора будет однозначным (с точность до множителя), если предполагать, что он
принадлежит подпространству, порожденному векторами
строится конструктивно. Выбор
вектора будет однозначным (с точность до множителя), если предполагать, что он
принадлежит подпространству, порожденному векторами  .
.
При построении будем
использовать алгоритм Шмидта. Он позволяет по последовательности линейно
независимых векторов  построить последовательность
построить последовательность  ортогональных
между собой векторов, обладающих следующим свойством. Вектор
ортогональных
между собой векторов, обладающих следующим свойством. Вектор  принадлежит
подпространству, порожденному векторами
принадлежит
подпространству, порожденному векторами  и ортогонален всем векторам,
расположенным в подпространстве, порожденном векторами
и ортогонален всем векторам,
расположенным в подпространстве, порожденном векторами  . Последовательность
. Последовательность  строится
рекуррентно. Положим
строится
рекуррентно. Положим  . Вектор
. Вектор  представим в виде:
представим в виде:  . Из условия
. Из условия  получим:
получим:  . Далее
полагаем
. Далее
полагаем  .
Вектор
.
Вектор  ортогонален
любому вектору из подпространства, порожденного векторами
ортогонален
любому вектору из подпространства, порожденного векторами  , которому принадлежат
векторы
, которому принадлежат
векторы  .
Следовательно
.
Следовательно  и
и  . Учитывая ортогональность векторов
. Учитывая ортогональность векторов
 ,
получаем:
,
получаем:  ,
,
 . На
. На  - ом шаге
алгоритма полагаем
- ом шаге
алгоритма полагаем
 . (15)
. (15)
Из условия 
 в силу ортогональности
векторов
в силу ортогональности
векторов 
 находим
находим  . Отметим
важное обстоятельство, что
. Отметим
важное обстоятельство, что
 . (16)
. (16)
Действительно, из (15) следует:

Пусть векторы  , где
, где  линейно независимы.
Построим проходящую через них гиперплоскость
линейно независимы.
Построим проходящую через них гиперплоскость  , т.е. такую гиперплоскость, для
которой
, т.е. такую гиперплоскость, для
которой  при
всех
при
всех  .
Используя алгоритм Шмидта, ортогонализируем последовательность векторов
.
Используя алгоритм Шмидта, ортогонализируем последовательность векторов  (легко видеть,
что они линейно независимы). Пусть последний элемент последовательности суть
(легко видеть,
что они линейно независимы). Пусть последний элемент последовательности суть  . Это и есть
искомый нормальный вектор. Действительно, по построению
. Это и есть
искомый нормальный вектор. Действительно, по построению  для
для  . Таким образом,
. Таким образом,  для всех
для всех  . В силу (16)
получаем
. В силу (16)
получаем  .
Используя это равенство, уравнение гиперплоскости можно переписать в виде:
.
Используя это равенство, уравнение гиперплоскости можно переписать в виде:  .
.
Зафиксируем произвольно  .
Гиперплоскость
.
Гиперплоскость  отделяет векторы
отделяет векторы  от нуля. Действительно,
от нуля. Действительно,  .
.
Рассмотрим задачу о разделении
гиперплоскостью множеств векторов  и
и  , для
, для  . Она разрешима в том и только том
случае, когда выпуклые оболочки
. Она разрешима в том и только том
случае, когда выпуклые оболочки  и
и  соответственно векторов
соответственно векторов  и
и  не
пересекаются. Пусть
не
пересекаются. Пусть  и
и  - векторы, на которых реализуется
минимальное расстояние между точками выпуклых оболочек
- векторы, на которых реализуется
минимальное расстояние между точками выпуклых оболочек  и
и  . Тогда разделение
множеств осуществляет любая гиперплоскость, которая ортогональна отрезку,
соединяющего векторы
. Тогда разделение
множеств осуществляет любая гиперплоскость, которая ортогональна отрезку,
соединяющего векторы  и
и  и проходит через его внутреннюю
точку.
и проходит через его внутреннюю
точку.
Нахождение векторов  и
и  - сложная
задача. Разделяющую гиперплоскость можно легко построить, если число
- сложная
задача. Разделяющую гиперплоскость можно легко построить, если число  и векторы
и векторы  ,
,  линейно
независимы (можно вычитать любой фиксированный вектор
линейно
независимы (можно вычитать любой фиксированный вектор  , или
, или  ). Рассмотрим
последовательность векторов
). Рассмотрим
последовательность векторов  ,
,  ,
,  . Они линейно независимы. Используя
алгоритм Шмидта, по данной последовательности построим ортогональную
последовательность. Пусть
. Они линейно независимы. Используя
алгоритм Шмидта, по данной последовательности построим ортогональную
последовательность. Пусть  - последний вектор, полученный в
процессе ортогонализации. По построению
- последний вектор, полученный в
процессе ортогонализации. По построению  для
для  ,
,  для
для  . Из равенства (16) следует, что
. Из равенства (16) следует, что  . Тем самым,
. Тем самым, 
 ,
, 
 . Кроме того,
. Кроме того,  . Обозначим:
. Обозначим:  и
и  . Пусть
. Пусть  .
Гиперплоскость
.
Гиперплоскость  разделяет векторы
разделяет векторы  и
и  . Действительно,
. Действительно,  ,
,  .
.
Отметим, что рассмотренный алгоритм выбора синаптических весов, основанный на ортогонализации входных векторов, - пример внешнего обучения нейрона Мак-Каллока Питтса.
Наследование признаков, сцепленных с полом
Хромосомный набор женских особей состоит из пар гомологичных хромосом. Мужские особи имеют две хромосомы (обозначим их как X и Y), которые не гомологичны ни одной другой хромосоме и, естественно, между собой. При этом хромосома X любой мужской особи имеет аналог у всех женских особей (хромосомы различаются визуально), а хромосомы Y у женских особей отсутствуют. Отсюда следует вывод, что пол оределяется хромосомной парой XY. Женские особи имеют две хромосомы X, а мужские имеют как хромосому X, так и хромосому Y. Мать передает своим детям хромосому X. От отца дочери переходит хромосома X, а сыну - хромосома Y. Для мужских особей аллель, расположенный в локусе хромосомы X, в принципе не имеет дополнения до аллельной пары. Относительно таких аллелей мужская особь не является ни гомо, ни гетерозиготной. О таких особях говорят, что они гемизиготны по соответствующим генам.
Гены расположенные в локусах
хромосом X и Y, называются сцеплеными с полом. Они были открыты в
1910 г. Т.Морганом. Эксперименты проводились с мухами дозофилами. Обычно цвет
глаз у этих мух - красный, реже встречаются мухи с белыми глазами. Т.Морган
скрещивал красноглазых самок с белоглазами самцами. Потомство в первом
поколении было красноглазым. Внешне ситуация полностью аналогична той, что
рассматривалась Г.Менделем. Скрещивание представителей двух разных гомозиготных
генотипов приводит к появлению гетерозиготных особей. Поскольку все мухи в
первом поколении имели краные глаза, этот цвет является доминантным. Согласно
Г.Менделю во втором поколениии этот цвет глаз должен наблюдаться с вероятностью
 , а белый
с вероятность
, а белый
с вероятность  . Это должно относиться как к
самцам, так и к самкам.
. Это должно относиться как к
самцам, так и к самкам.
Результаты опытов Т.Моргана
оказались иными. Во втором поколении действительно у  мух наблюдались красные глаза.
Однако, половина самцов имели красные, а вторая половина - белые глаза.
Поскольку женские и мужские особи отличаются наборами хромосом X и Y,
следует предположить, что аллель ответственный за цвет глаз располагается в
локусе одной их них. Таковой не может быть хромосома Y, так как она
отсутствует у женских особей. Следовательно, соответствующий ген раположен в
локусе хромосомы X. Обозначим аллель, обуславливающий красный цвет глаз
как A, а белый - как a. Существует три женских генотипа AA,
Aa, aa и два мужских: A и a. Скрещивание самок
дрозофил генотипа AA и самцов генотипа a приводит к появлению в
первом поколении потомства с красными глазами. Генотип самок - Aa, а
самцов - A. Во втором поколении рождаются только красноглазые самки
(генотипы AA, Aa). Мужские особи с вероятностью
мух наблюдались красные глаза.
Однако, половина самцов имели красные, а вторая половина - белые глаза.
Поскольку женские и мужские особи отличаются наборами хромосом X и Y,
следует предположить, что аллель ответственный за цвет глаз располагается в
локусе одной их них. Таковой не может быть хромосома Y, так как она
отсутствует у женских особей. Следовательно, соответствующий ген раположен в
локусе хромосомы X. Обозначим аллель, обуславливающий красный цвет глаз
как A, а белый - как a. Существует три женских генотипа AA,
Aa, aa и два мужских: A и a. Скрещивание самок
дрозофил генотипа AA и самцов генотипа a приводит к появлению в
первом поколении потомства с красными глазами. Генотип самок - Aa, а
самцов - A. Во втором поколении рождаются только красноглазые самки
(генотипы AA, Aa). Мужские особи с вероятностью  относятся к генотипам A
и a, т.е. половина имеет красный, а половина - белый цвет глаз. Если
считать, что число самок и самцов одинаково, то суммарно во втором поколении
частота красноглазых особей
относятся к генотипам A
и a, т.е. половина имеет красный, а половина - белый цвет глаз. Если
считать, что число самок и самцов одинаково, то суммарно во втором поколении
частота красноглазых особей  . Таким образом, результаты опытов
Т.Моргана находят объяснение.
. Таким образом, результаты опытов
Т.Моргана находят объяснение.
На мужской хромосоме
локализуется очень мало генов, что весьма рацианально. Сцепленный с хромосомой Y
ген, а, следовательно, и признак, имеют только мужские особи. Передается он
только по мужской линии. На женской хромосоме Y локализуется много
генов. Цветовое зрение у человека контролируется только аллелями, сцепленными с
X - хромосомой. Через эту хромосому передается дальтонизм (отсутствие
цветового зрения). У женщин дальтонизм проявляется, если она получила два
соответствующих аллеля (данные аллели рецессивны). Мужчине достаточно одного
такого гена. В результате дальтонизм у мужчин встречается чаще, чем у женщин.
Если у женщины отсутствует цветовое зрение, то ее сын будет дальтоником, а у
дочери дальтонизм будет только, если он наблюдается еще и у отца. Если женщина является
скрытым носителем дальтонизма (относится к гетерозиготному генотипу), то ее сын
наследует дальтонизм с вероятностью  . Отметим еще, что тяжелое
заболевание - гемофилия (плохая свертываемость крови) также вызывается геном,
сцепленным с X -хромосомой.
. Отметим еще, что тяжелое
заболевание - гемофилия (плохая свертываемость крови) также вызывается геном,
сцепленным с X -хромосомой.
Рассмотрим вопрос об эволюции
частот генов, сцепленных с X -хромосомой. Необходимо отслеживать женскую
и мужскую линии, которые, естественно, связаны между собой. Как уже говорилось,
в популяции по X -сцепленному гену с двумя аллелями A и a
присутствует три женских: AA, Aa, aa и два мужских: A,
a генотипа. Обозначим женских частоты генотипов в i -ом поколении через  и
соответственно мужских -
и
соответственно мужских -  . Как обычно выполнены соотношения:
. Как обычно выполнены соотношения:
 ,
,  . Пусть
. Пусть  -частоты
женских гамет в i -ом поколении. Они связаны с частотами генотипов обычными для
случая двухаллельного локуса формулами:
-частоты
женских гамет в i -ом поколении. Они связаны с частотами генотипов обычными для
случая двухаллельного локуса формулами:
 ,
,  , (7)
, (7)
 ,
,  ,
,  . (8)
. (8)
Очевидно, что частоты мужских гамет и генотипов совпадают. Поскольку женские особи получают от родителей одну женскую и одну мужскую гаметы, для следующего i+1 -ого поколения имеем следующие частоты женских генотипов.
Генотип Частота






Легко проверяется, что

Из равенства (7) в силу формул для частот женских генотипов в i+1 -ом поколении получаем соотношения для частот женских гамет в i+1 -ом поколении:

 , (9)
, (9)

 . (10)
. (10)
Потомки мужского пола получают
аллели A и a через женскую гамету. Следовательно, частоты  и
и  генотипов A
и a (они же -частоты гамет) совпадают с частотами
генотипов A
и a (они же -частоты гамет) совпадают с частотами  и
и  женских гамет в i -ом
поколении. В силу данного обстоятельства и формул (9), (10) получаем следующие
уравнения для эволюции частот женских и мужских гамет:
женских гамет в i -ом
поколении. В силу данного обстоятельства и формул (9), (10) получаем следующие
уравнения для эволюции частот женских и мужских гамет:
 ,
,  , (11)
, (11)
 ,
,  . (12)
. (12)
Решим систему разностных уравнений (11) описанным выше способом. Выпишем матрицу правых частей:

Ее собственные значения определяются из характеристического уравнения

Раскрывая определитель, получаем

Находим корни:  и
и  . Собственные векторы
. Собственные векторы  ,
,  -
нетривиальные решения систем:
-
нетривиальные решения систем:
 ,
,  ,
,
из которых следует, что
 ,
,  .
.
Система разностных уравнений
(11) имеет частные решения  и
и  . Общим решением системы является
их линейная комбинация:
. Общим решением системы является
их линейная комбинация:
 .
.
Из начального условия

определяем константы  и
и  . В результате
получаем явную зависимость частот женских и мужских гамет A от номера
поколения:
. В результате
получаем явную зависимость частот женских и мужских гамет A от номера
поколения:
 ,
,
 .
.
Совершенно аналогично из (12) для частот женских и мужских гамет a получаем:
 ,
,
 .
.
Используя полученные формулы
для эволюции частот, сделаем ряд выводов. Положим: 
 ,
,  . Отметим, что
. Отметим, что  . С ростом номера
поколения частоты женских и мужских гамет A стремятся к общему пределу
. С ростом номера
поколения частоты женских и мужских гамет A стремятся к общему пределу  ,
соответственно частоты гамет a стремятся к пределу
,
соответственно частоты гамет a стремятся к пределу  . Последовательности
частот сходятся немонотонно, но со скоростью геометрической прогрессии, т.е.
весьма быстро. Напомним, что в i -ом поколении частоты женских генотипов AA,
Aa, aa суть
. Последовательности
частот сходятся немонотонно, но со скоростью геометрической прогрессии, т.е.
весьма быстро. Напомним, что в i -ом поколении частоты женских генотипов AA,
Aa, aa суть  ,
,  ,
,  .
.
Отсюда следует, что в пределе
 ,
,  ,
,  .
.
Таким образом, для женских
генотипов в пределе имеет место закон Харди -Вайнберга. Так как сходимость к
пределу очень быстрая, то на практике можно считать, что после смены трех
-четырех поколений частоты женских генотипов AA, Aa, aa
суть  ,
,  ,
,  . Аналогично,
частоты мужских генотипов A и a после смены нескольких поколений
приближенно равны
. Аналогично,
частоты мужских генотипов A и a после смены нескольких поколений
приближенно равны  и
и  .
.
Напомним, что гены дальтонизма
и гемофилии являются рецессивными. Согласно полученным результатам, сцепленный
с полом дефект, который встречается у мужчин с вероятностью  , у женщин проявляется с
гораздо меньшей вероятностью
, у женщин проявляется с
гораздо меньшей вероятностью  .
.
Отбор в менделевской бесполой диплоидной популяции
Закон Харди -Вайнберга гласит, что при отсутствии возмущений частоты аллелей не изменяются. Однако процессы, изменяющие частоты генов, постоянно происходят в популяции. Без них не было бы эволюции. Рассмотрим процессы отбора. К идее естественного отбора как основного процесса в эволюции пришли независимо друг от друга Чарльз Дарвин и Альфред Рассел Уоллес. В 1858 г. на заседании Линнеевского общества в Лондоне были представлены сообщения об их открытии. Доказательства того, что эволюция происходит путем естественного отбора были даны Ч. Дарвином в его работе "Происхождение видов" в 1859 г. Ч. Дарвин предположил, что в результате изменений появляются наследуемые признаки, которые обеспечивают их обладателям лучшую приспособленность к условиям среды. Такие организмы имеют больше шансов к выживанию и оставляют больше потомства, чем особи наделенные менее полезными свойствами. В результате частота признаков, обеспечивающих лучшую приспособленность (адаптивность), будет увеличиваться от поколения к поколению за счет частоты признаков, дающих меньшую адаптивность. Этот процесс был назван естественным отбором.
Рассмотрим простейший случай -
модель отбора в двухаллельной менделевской популяции. В ее основе лежит закон
Харди -Вайнберга расчета частот аллелей и генотипов. Припишем генотипам AA,
Aa, aa числа  ,
,  ,
,  , которые назовем относительными
приспособленностями. Данные коэффициенты можно интерпретировать как вероятности
того, что особь соответствующего генотипа доживает до этапа размножения.
Обозначим через
, которые назовем относительными
приспособленностями. Данные коэффициенты можно интерпретировать как вероятности
того, что особь соответствующего генотипа доживает до этапа размножения.
Обозначим через  и
и  частоты
частоты  аллелей A и a в n -ом
поколении в момент его появления (они же - частоты гамет n-1 ого поколения).
Первоначально для n -ого поколения согласно закону Харди -Вайнберга для
генотипов AA, Aa, aa имеем частоты:
аллелей A и a в n -ом
поколении в момент его появления (они же - частоты гамет n-1 ого поколения).
Первоначально для n -ого поколения согласно закону Харди -Вайнберга для
генотипов AA, Aa, aa имеем частоты:  ,
,  ,
,  . Числа
. Числа  ,
,  ,
,  есть вероятности того,
что особь n -ого поколения относится соответственно к генотипу AA, Aa,
aa и доживает до этапа размножения. Полная вероятность того, что особь n
- ого поколения доживает до размножения суть
есть вероятности того,
что особь n -ого поколения относится соответственно к генотипу AA, Aa,
aa и доживает до этапа размножения. Полная вероятность того, что особь n
- ого поколения доживает до размножения суть
 . (13)
. (13)
Эту величину будем называть средней приспособленностью в n -ом поколении. Используя формулу Бейеса (теорема гипотез), выписываем частоты генотипов AA, Aa, aa этого поколения к моменту начала этапа размножения:
 ,
,  ,
,  .
.
Частоты гамет A, a определяются частотами генотипов:
 ,
,  .
.
Частоты аллелей A, a в момент появления n+1 -ого поколения совпадают с частотами гамет предыдущего поколения. Получаем уравнения связывающие частоты аллелей:
 , (14)
, (14)
 . (15)
. (15)
Независимым из этих двух
уравнений является только одно т.к.  . Отметим, что уравнения (14) и
(15) не меняются, если заменить
. Отметим, что уравнения (14) и
(15) не меняются, если заменить  , где
, где  произвольно. В связи с этим часто
принимают равной единице максимальную относительную приспособленность.
произвольно. В связи с этим часто
принимают равной единице максимальную относительную приспособленность.
Уравнение (14) имеет явные
решения только в частных случаях. Рассмотрим случай так называемого геометрического
отбора. Пусть относительные приспособленности генотипов образуют
геометрическую прогрессию:  ,
,  ,
,  . Введем обозначения
. Введем обозначения  . Разделив
первое уравнение на второе, получим
. Разделив
первое уравнение на второе, получим
 .
.
Отсюда следует, что  . Вернемся к
старым переменным:
. Вернемся к
старым переменным:
 .
.
Получаем
 .
.
Если  , то отбора нет,
, то отбора нет,  и для всех
и для всех  . Если
. Если  , то
, то  и
и  с ростом
с ростом  , т.е. аллель A
вытесняет аллель a. Если
, т.е. аллель A
вытесняет аллель a. Если  , то наоборот -аллель a
вытесняет аллель A. Отбор геометрического типа эквивалентен отбору на
уровне аллелей. Действительно, пусть
, то наоборот -аллель a
вытесняет аллель A. Отбор геометрического типа эквивалентен отбору на
уровне аллелей. Действительно, пусть  - вероятность того что, особь,
имеющая один аллель A, доживет до стадии размножения. В свою очередь,
пусть
- вероятность того что, особь,
имеющая один аллель A, доживет до стадии размножения. В свою очередь,
пусть  аналогичная
вероятность по аллелю a. Данные вероятности можно понимать как
вероятности выживания аллелей и можно назвать приспособленностью аллелей. Если
считать, что гибель аллеля приводит к гибели особи, то вероятности выживания
(приспособленности) особей генотипов AA, Aa, aa суть
аналогичная
вероятность по аллелю a. Данные вероятности можно понимать как
вероятности выживания аллелей и можно назвать приспособленностью аллелей. Если
считать, что гибель аллеля приводит к гибели особи, то вероятности выживания
(приспособленности) особей генотипов AA, Aa, aa суть  ,
,  ,
,  . Как уже
отмечалось, приспособленности можно нормировать (разделить на одно и то же
число). После деления на
. Как уже
отмечалось, приспособленности можно нормировать (разделить на одно и то же
число). После деления на  получим приспособленности генотипов
получим приспособленности генотипов
 ,
,  ,
,  , где
, где  .
.
Рассмотрим случай летального
гена. Когда говорят о летальности рецессивного аллеля a, то это не
обязательно означает, что генотипы aa умирают. Они считаются генетически
летальными, если не оставляют потомков. Пусть  и
и  . Уравнения (14), (15) имеют вид:
. Уравнения (14), (15) имеют вид:
 ,
,  ,
,
или же
 ,
,  .
.
Можно найти в явном виде
решение второго уравнения. Положим  . Тогда
. Тогда
 .
.
Общее решение разностного
уравнения  ищут
в виде
ищут
в виде  .
После подстановки получаем:
.
После подстановки получаем:  . Отсюда, используя метод
неопределенных коэффициентов, выводим
. Отсюда, используя метод
неопределенных коэффициентов, выводим  и
и  , т. е.
, т. е.  . В силу начального условия
. В силу начального условия  получаем
получаем  . Для исходной
переменной
. Для исходной
переменной  имеем
формулу
имеем
формулу  ,
из которой следует, что частота летального аллеля с ростом номера поколения
стремится к нулю, т. е. он исчезает. Отметим, что процесс очень медленный, Так
при
,
из которой следует, что частота летального аллеля с ростом номера поколения
стремится к нулю, т. е. он исчезает. Отметим, что процесс очень медленный, Так
при  требуется
десять поколений, чтобы наполовину сократить частоту гена.
требуется
десять поколений, чтобы наполовину сократить частоту гена.
Сказанному можно дать еще следующую интерпретацию. Предположим, что проводится селекционная работа по искоренению рецессивного аллеля a, который признан нежелательным в популяции. Этот аллель имеет внешние проявления только у особей генотипа aa. Они не допускаются к размножению. Данная селекционная стратегия малоэффективна, что следует из приведенного выше примера. Как только селекционная программа прекращается, частоты аллелей перестают меняться, что вытекает из закона Харди -Вайнберга. Если бы какой-нибудь сумасшедший диктатор по совету своего не менее безумного окружения решил извести альбиносов (частота соответствующего аллеля 0.01), то за одно -два поколения (продолжительность жизни диктатора) значение частоты аллеля не изменилось бы во втором знаке.
Рассмотрим случай, когда
различны относительные приспособленности  и
и  генотипов AA, Aa, и,
одновременно, аллель a является летальным, т. е.
генотипов AA, Aa, и,
одновременно, аллель a является летальным, т. е.  . Тогда
. Тогда
 ,
,  .
.
Полагая  , получим
, получим
 .
.
В отличии от предыдущего, общее
решение этого уравнения ищем в виде:  . После подстановки получим
. После подстановки получим  . Метод
неопределенных коэффициентов дает
. Метод
неопределенных коэффициентов дает  и
и  , т.е.
, т.е.  . Из начального условия
. Из начального условия  следует, что
следует, что  . Переменные
. Переменные  вводились
равенствами
вводились
равенствами  , из которых
, из которых
 ,
,
 .
.
Пусть  , т.е. относительная
приспособленность гомозиготного генотипа AA выше чем гетерозиготного
генотипа Aa. Тогда
, т.е. относительная
приспособленность гомозиготного генотипа AA выше чем гетерозиготного
генотипа Aa. Тогда  и
и  при
при  , т.е. с ростом номера поколения
аллель a, а, следовательно, и генотип Aa вытесняется из
популяции.
, т.е. с ростом номера поколения
аллель a, а, следовательно, и генотип Aa вытесняется из
популяции.
В случае, когда  , приспособленность
гетерозигот Aa больше приспособленности гетерозигот AA. Ясно, что
, приспособленность
гетерозигот Aa больше приспособленности гетерозигот AA. Ясно, что
 при
при  и частоты
и частоты  ,
,  стремятся к
отличным от нуля и единицы пределам:
стремятся к
отличным от нуля и единицы пределам:
 ,
,  .
.
Таким образом, хотя аллель a является летальным, оба генотипа AA и Aa сосуществуют. Этот результат первоначально кажется парадоксальным. Однако, предсказанный теорией факт сосуществования генотипов, один из которых имеет летальный аллель, обнаружен в природных популяциях. Аллель серповидно клеточного гемоглобина летален и одновременно встречается у миллионов людей в Африке. Широкое распространение гетерозигот объясняется их повышенной сопротивляемостью к малярии.
Исследование эволюционных уравнений
Уравнение (14) имеет вид:
 , (16)
, (16)
где непрерывно дифференцируемая функция
 (17)
(17)
задает одномерное
отображение  . Последовательность итераций
. Последовательность итераций  будем называть
траекторией отображения
будем называть
траекторией отображения  . Ставится задача об исследовании
траекторий.
. Ставится задача об исследовании
траекторий.
Пусть отображение  имеет
неподвижную точку
имеет
неподвижную точку  , т.е.
, т.е.  . Простейшей траекторией является
стационарная последовательность
. Простейшей траекторией является
стационарная последовательность  . Она же называется состоянием
равновесия уравнения (16). Говорят, что состояние равновесия устойчиво
(асимптотически), если существует такая его окрестность, что все траектории
начинающиеся в ней сходятся к состоянию равновесия. Для устойчивости состояния
равновесия
. Она же называется состоянием
равновесия уравнения (16). Говорят, что состояние равновесия устойчиво
(асимптотически), если существует такая его окрестность, что все траектории
начинающиеся в ней сходятся к состоянию равновесия. Для устойчивости состояния
равновесия  достаточно
достаточно
 при
при  . Наоборот,
если
. Наоборот,
если  при
при  , то состояние
равновесия неустойчиво. Это означает, что в сколь угодно малой окрестности
состояния равновесия берет начало траектория, которая с ростом номера n покинет
некоторую фиксированную окрестность состояния равновесия. Траектория может
сколько угодно раз возвращаться в эту окрестность, но каждый раз после
возвращения снова покидает ее.
, то состояние
равновесия неустойчиво. Это означает, что в сколь угодно малой окрестности
состояния равновесия берет начало траектория, которая с ростом номера n покинет
некоторую фиксированную окрестность состояния равновесия. Траектория может
сколько угодно раз возвращаться в эту окрестность, но каждый раз после
возвращения снова покидает ее.
Одномерные отображения (но не
(17)) могут иметь периодические траектории:  , где
, где  - минимальный период. Периодические
траектории (циклы) есть неподвижные точки отображения, задаваемого сложной
функцией
- минимальный период. Периодические
траектории (циклы) есть неподвижные точки отображения, задаваемого сложной
функцией  .
В частности, циклы периода два - неподвижные точки отображения
.
В частности, циклы периода два - неподвижные точки отображения  . Циклы устойчивы или
неустойчивы в зависимости от того, устойчивы или неустойчивы соответствующие
неподвижные точки. Известны отображения, которые имеют неустойчивые циклы
любого периода. Поведение траекторий таких отображений чрезвычайно сложно.
Приближенно говоря, трактории пробегают вблизи любого цикла. Тем самым, задача
о поведении траекторий одномерного отображения весьма не проста.
. Циклы устойчивы или
неустойчивы в зависимости от того, устойчивы или неустойчивы соответствующие
неподвижные точки. Известны отображения, которые имеют неустойчивые циклы
любого периода. Поведение траекторий таких отображений чрезвычайно сложно.
Приближенно говоря, трактории пробегают вблизи любого цикла. Тем самым, задача
о поведении траекторий одномерного отображения весьма не проста.
Однако, в рассматриваемом конкретном случае отображения, заданного формулой (17), все траектории стремятся к состояниям равновесия. Доказательство этого утверждения будет нашей ближайшей задачей.
Покажем сначала, что функция  , заданная
формулой (17), монотонно растет на интервале
, заданная
формулой (17), монотонно растет на интервале  . Запишем функцию
. Запишем функцию  в виде:
в виде:  , где
, где
 ,
,  .
.
Здесь  для
для  .
.
Легко получаем
 .
.
В свою очередь, для ![]()
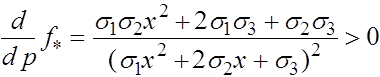 .
.
Таким образом,
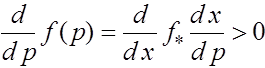
для ![]() и
функция монотонно растет.
и
функция монотонно растет.
Из монотонности функции
вытекает важное следствие. Пусть ![]() и
и
![]()
![]() -
два состояния равновесия и на интервале
-
два состояния равновесия и на интервале ![]() других
состояний равновесия нет. Предположим, что начальная точка траектории
других
состояний равновесия нет. Предположим, что начальная точка траектории ![]() . тогда при
. тогда при ![]() точки траектории стремятся
к одному из состояний равновесия: или к
точки траектории стремятся
к одному из состояний равновесия: или к ![]() ,
или к
,
или к ![]() .
.
Для доказательства заметим
сначала, что отображение ![]() переводит
отрезок
переводит
отрезок ![]() в себя. Действительно. в
силу монотонности для любого
в себя. Действительно. в
силу монотонности для любого ![]() имеем
имеем ![]() и
и ![]() , т.е.
, т.е. ![]() . Далее, так как на
интервале
. Далее, так как на
интервале ![]() нет состояний равновесия
(точек, где
нет состояний равновесия
(точек, где ![]() ), то либо
), то либо ![]() либо
либо ![]() для
для ![]() . Пусть реализуется первый
случай. Тогда
. Пусть реализуется первый
случай. Тогда ![]() .
Последовательность
.
Последовательность ![]() монотонно растет
и ограничена сверху числом
монотонно растет
и ограничена сверху числом ![]() . Она
сходится. Переходя в равенстве
. Она
сходится. Переходя в равенстве ![]() к
пределу при
к
пределу при ![]() получим
получим ![]() . Поскольку на интервале
. Поскольку на интервале ![]() отсутствуют состояния
равновесия то
отсутствуют состояния
равновесия то ![]() , т.е.
, т.е. ![]() . Аналогично проверяется,
что в случае
. Аналогично проверяется,
что в случае ![]() для
для ![]() точки траектории
точки траектории ![]() . Тем самым,
сформулированное следствие доказано.
. Тем самым,
сформулированное следствие доказано.
Доказательство того, что все
траектории отображения (17) стремятся к состояниям равновесия теперь легко
завершается. Заметим, что крайние точки![]() и
и
![]() отрезка
отрезка ![]() являются неподвижными для
отображения (17). Если отображение не имеет других неподвижных точек, то все
его траектории стремятся к одной и той же неподвижной точке (либо
являются неподвижными для
отображения (17). Если отображение не имеет других неподвижных точек, то все
его траектории стремятся к одной и той же неподвижной точке (либо ![]() , либо
, либо ![]() . Если существуют другие
неподвижные точки, то они разбивают отрезок
. Если существуют другие
неподвижные точки, то они разбивают отрезок ![]() на
части. Внутри каждой из частей все траектории стремятся к одной из крайних
точек разбиения.
на
части. Внутри каждой из частей все траектории стремятся к одной из крайних
точек разбиения.
Состояния равновесия определяются из уравнения:
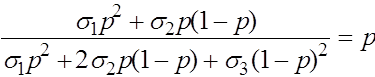 .
.
Последовательно получаем:
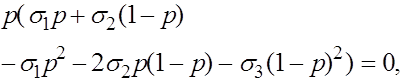
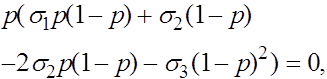
![]()
Отсюда получаем, что кроме
найденных ранее состояний равновесия ![]() и
и ![]() может присутствовать еще
одно:
может присутствовать еще
одно:
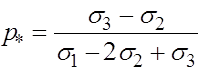 .
(18)
.
(18)
Соответствующее значение
частоты ![]() суть
суть
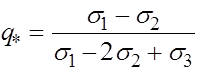 .
(19)
.
(19)
Поскольку ![]() и
и ![]() , то состояние равновесия
(18) существует, если выполнено одно из условий:
, то состояние равновесия
(18) существует, если выполнено одно из условий:
![]() ,
,
![]() ,
(20)
,
(20)
![]() ,
,
![]() .
(21)
.
(21)
В состояниях равновесия ![]() и
и ![]() генофонд популяции содержит
соответственно только аллели A и a. Равновесное состояние, если
оно существует, соответствует случаю, когда генофонд содержит оба аллеля. Оно
называется равновесным пилиморфизмом.
генофонд популяции содержит
соответственно только аллели A и a. Равновесное состояние, если
оно существует, соответствует случаю, когда генофонд содержит оба аллеля. Оно
называется равновесным пилиморфизмом.
Ниже нам потребуются
значения производной 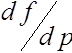 при
при ![]() и
и ![]() . Прямые вычисления
показывают, что
. Прямые вычисления
показывают, что
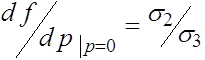 ,
, 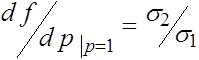 . (22)
. (22)
Возможны четыре случая соотношений относительных приспособленностий генотипов:
1. ![]() ,
,
2. ![]() ,
,
3. ![]() ,
, ![]() ,
,
4. ![]() ,
, ![]() .
.
Первый случай. Следует
предполагать, что одно из неравенств строгое, в противном случае нет отбора.
Поскольку либо ![]() , либо
, либо ![]() , то отсутствует внутреннее
равновесное состояние
, то отсутствует внутреннее
равновесное состояние ![]() и
и ![]() для частот аллелей,
заданных формулами (18) и (19). Действительно, одно из этих чисел будет отрицательным.
В силу проведенных выше рассуждений все траектории отображения
для частот аллелей,
заданных формулами (18) и (19). Действительно, одно из этих чисел будет отрицательным.
В силу проведенных выше рассуждений все траектории отображения ![]() стремятся к одному из
крайних равновесных состояний: либо
стремятся к одному из
крайних равновесных состояний: либо ![]() , либо
, либо ![]() . Разность
. Разность ![]() не обращается в ноль, а,
следовательно, не меняет знак на интервале
не обращается в ноль, а,
следовательно, не меняет знак на интервале ![]() .
Если она положительна, то траектории стремятся к состоянию равновесия
.
Если она положительна, то траектории стремятся к состоянию равновесия ![]() . В противном случае
траектории стремятся к нулевому состоянию равновесия. Знак разности можно
определить, анализируя ее в малых окрестностях состояний равновесия. Пусть для
определенности
. В противном случае
траектории стремятся к нулевому состоянию равновесия. Знак разности можно
определить, анализируя ее в малых окрестностях состояний равновесия. Пусть для
определенности ![]() . Тогда из формулы
Тейлора и (22) следует, что
. Тогда из формулы
Тейлора и (22) следует, что
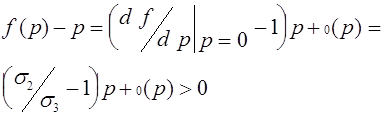
для ![]() .
Совершенно аналогично проверяется, что для случая
.
Совершенно аналогично проверяется, что для случая ![]() данная
разность положительна при
данная
разность положительна при ![]() .
.
Таким образом, все
траектории отображения стремятся к состоянию равновесия ![]() . Происходит вытеснение
менее приспособленного аллеля a из популяции. Однако этот процесс
протекает очень медленно. Пусть, например,
. Происходит вытеснение
менее приспособленного аллеля a из популяции. Однако этот процесс
протекает очень медленно. Пусть, например, ![]() и
и
![]() , где
, где ![]() . Тогда можно показать, что
. Тогда можно показать, что ![]() , при
, при ![]() .
.
Второй случай полностью симметричен первому. Происходит медленное вытеснение аллеля A.
Третий случай. Выполнено
условие (21), при котором существует внутреннее состояние равновесия ![]() , определенное формулой (18).
Выясним, какие знаки имеет разность
, определенное формулой (18).
Выясним, какие знаки имеет разность ![]() на
интервалах
на
интервалах ![]() и
и ![]() . Для
. Для ![]() как и в первом случае имеем
как и в первом случае имеем
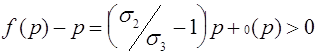 ,
,
следовательно ![]() для всех
для всех ![]() . Траектория с начальным
условием
. Траектория с начальным
условием ![]() стремится к состоянию равновесия
стремится к состоянию равновесия
![]() . Состояние равновесия
. Состояние равновесия ![]() неустойчиво.
неустойчиво.
В свою очередь для значений ![]() по формуле Тейлора
получаем:
по формуле Тейлора
получаем:
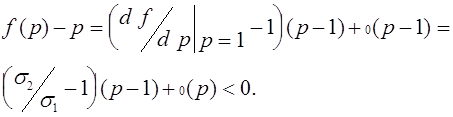
Для всех ![]() выполнено неравенство
выполнено неравенство ![]() . Траектории с начальным
условием
. Траектории с начальным
условием ![]() также стремятся к
внутреннему состоянию равновесия
также стремятся к
внутреннему состоянию равновесия ![]() , а
состояние равновесия
, а
состояние равновесия ![]() неустойчиво.
неустойчиво.
Итак, в рассматриваемом случае независимо от начальных условий все траектории стремятся к устойчивому состоянию равновесия:
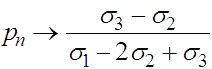 ,
, 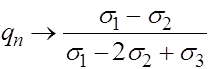 .
.
Популяция эволюционизирует к этому состоянию. В ней присутствуют все генотипы AA, Aa, aa, включая менее приспособленные. Как уже отмечалось, такое состояние называется балансированным полиморфизмом.
Четвертый случай. Здесь
также существует внутреннее состояние равновесия ![]() .
Однако, знаки функции
.
Однако, знаки функции ![]()
![]() на интервалах
на интервалах ![]() и
и ![]() будут противоположными тем,
которые имели место в третьем случае:
будут противоположными тем,
которые имели место в третьем случае: ![]() для
для
![]() и
и ![]() для
для ![]() . Вследствие этого, для
траекторий с начальными условиями
. Вследствие этого, для
траекторий с начальными условиями ![]() получаем
получаем
![]() при
при ![]() (соответственно
(соответственно ![]() ). Аллель A
вытесняется из популяции. Если же
). Аллель A
вытесняется из популяции. Если же ![]() , то
, то ![]() и
и ![]() при
при ![]() . Постепенно вытесняется из
популяции аллель a. Какой аллель теряется - зависит от начального
состояния популяции. Равновесный полиморфизм оказывается неустойчивым.
. Постепенно вытесняется из
популяции аллель a. Какой аллель теряется - зависит от начального
состояния популяции. Равновесный полиморфизм оказывается неустойчивым.
Поведение траектории ![]() можно изобразить в виде
фазовой диаграммы, где вдоль оси абсцисс откладывается значение
можно изобразить в виде
фазовой диаграммы, где вдоль оси абсцисс откладывается значение ![]() , а вдоль оси ординат -
величина
, а вдоль оси ординат -
величина ![]() .
.
Диаграммы a), b), c), d) соответствуют случаям 1- 4.
Возрастание средней приспособленности
Выше средней приспособленностью
в n -ом поколении была названа величина ![]() .
Она интерпретировалась, как полная вероятность того, что особь n -ого
поколения доживает до этапа размножения. Покажем, что средняя приспособленность
-неубывающая функция от номера поколения n. Таким образом, эволюция
происходит в сторону возрастания приспособленности популяции, что полностью
соответствует теории Ч. Дарвина.
.
Она интерпретировалась, как полная вероятность того, что особь n -ого
поколения доживает до этапа размножения. Покажем, что средняя приспособленность
-неубывающая функция от номера поколения n. Таким образом, эволюция
происходит в сторону возрастания приспособленности популяции, что полностью
соответствует теории Ч. Дарвина.
Запишем ![]() как функцию от
как функцию от ![]() :
:
![]()
и вычислим ее производные:
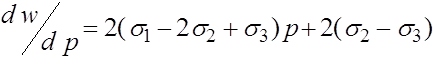 ,
,
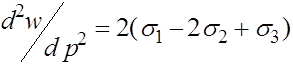 .
.
Таким образом, экстремальное
значение ![]() достигается при
достигается при
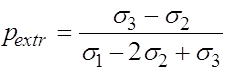 (23)
(23)
и является максимумом при ![]() и минимумом, если
и минимумом, если ![]() .
.
Рассмотрим первый случай,
когда ![]() . Квадратичная функция
. Квадратичная функция ![]() не имеет экстремума на
интервале
не имеет экстремума на
интервале ![]() . Действительно, пусть для
определенности
. Действительно, пусть для
определенности ![]() . Тогда из (23)
следует, что экстремальная точка
. Тогда из (23)
следует, что экстремальная точка ![]() . Для
всего интервала
. Для
всего интервала ![]() производная
производная 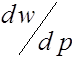 имеет один и тот же знак.
При
имеет один и тот же знак.
При ![]() имеем
имеем 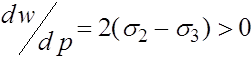 . Следовательно, функция
. Следовательно, функция ![]() на интервале
на интервале ![]() монотонно растет. Напомним,
что в рассматриваемом случае для траектории
монотонно растет. Напомним,
что в рассматриваемом случае для траектории ![]() отображения
отображения
![]() также монотонно
также монотонно ![]() при
при ![]() . В результате
. В результате ![]() . При этом
. При этом ![]() .
.
Второй случай ![]() подобен первому. Функция
подобен первому. Функция ![]() на интервале
на интервале ![]() не имеет экстремума и
монотонно убывает. Согласно полученным ранее результатам, для траектории
отображения имеем:
не имеет экстремума и
монотонно убывает. Согласно полученным ранее результатам, для траектории
отображения имеем: ![]() . В результате
последовательность
. В результате
последовательность ![]() оказывается
монотонно растущей:
оказывается
монотонно растущей: ![]() . При этом
. При этом ![]() при
при ![]() .
.
В третьем случае (![]() ,
, ![]() ) экстремальная точка
) экстремальная точка ![]() является точкой максимума,
т.к.
является точкой максимума,
т.к.
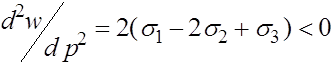 .
.
На интервале ![]() функция
функция ![]() монотонна растет, а на
интервале
монотонна растет, а на
интервале ![]() монотонно убывает.
Одновременно, точка
монотонно убывает.
Одновременно, точка ![]() , согласно (18),
является устойчивым состоянием равновесия
, согласно (18),
является устойчивым состоянием равновесия ![]() (состояние
полиморфизма). Как показано выше, если начальная точка траектории
(состояние
полиморфизма). Как показано выше, если начальная точка траектории ![]() , то для всех ее точек
, то для всех ее точек ![]() . Тем самым,
последовательность
. Тем самым,
последовательность ![]() монотонно растет.
Если же начальная точка
монотонно растет.
Если же начальная точка ![]() , то
, то ![]() . Тем не менее,
последовательность
. Тем не менее,
последовательность ![]() по-прежнему
монотонно растет, в силу монотоного убывания функции
по-прежнему
монотонно растет, в силу монотоного убывания функции ![]() на соответствующем
интервале.
на соответствующем
интервале.
Четвертый случай (![]() ,
, ![]() ) аналогичен предыдущему.
Состояние неустойчивого полиморфизма является точкой минимума для средней
приспособленности. Траектории (последовательности
) аналогичен предыдущему.
Состояние неустойчивого полиморфизма является точкой минимума для средней
приспособленности. Траектории (последовательности ![]() )
с начальными условиями
)
с начальными условиями ![]() монотонно
убывают. Одновременно, на соответствующем промежутке также монотонно убывает
функция
монотонно
убывают. Одновременно, на соответствующем промежутке также монотонно убывает
функция ![]() . В результате
последовательность
. В результате
последовательность ![]() монотонно растет.
Если же
монотонно растет.
Если же ![]() , то последовательность
, то последовательность ![]() монотонно растет, а вместе
с ней и последовательность
монотонно растет, а вместе
с ней и последовательность ![]() , т.к.
функция
, т.к.
функция ![]() для
для ![]() монотонно растет.
монотонно растет.
Рисунок иллюстрирует направление поведение средней приспособленности в рассмотренных случаях.
Отметим, что возрастание
средней приспособленности можно доказать непосредственно, не разбирая в
отдельности каждый случай. Далее, поскольку средняя приспособленность есть
ограниченная величина, можно сделать вывод, что последовательность ![]() имеет предел при
имеет предел при ![]() . Используя этот факт, еще
одним способом можно показать, что все траектории отображения сходятся к
состояниям равновесия. Такой прием иногда используется для анализа разностных
уравнений. Функцию
. Используя этот факт, еще
одним способом можно показать, что все траектории отображения сходятся к
состояниям равновесия. Такой прием иногда используется для анализа разностных
уравнений. Функцию ![]() пытаются
подобрать, используя специфику уравнения. Часто ее называют функцией Ляпунова.
Естественно, что функции Ляпунова не всегда существуют. Как уже отмечалось,
поведения траекторий может быть весьма сложным. В частности, может оказаться,
что уравнение не имеет устойчивых состояний равновесия.
пытаются
подобрать, используя специфику уравнения. Часто ее называют функцией Ляпунова.
Естественно, что функции Ляпунова не всегда существуют. Как уже отмечалось,
поведения траекторий может быть весьма сложным. В частности, может оказаться,
что уравнение не имеет устойчивых состояний равновесия.
Мутации
Наследственная передача признаков от родителей к потомству -консервативный процесс, хотя эта консервативность не является абсолютной. В противном случае не возможна была бы эволюция. Иногда при воспроизводстве гамет (половых клеток) происходят “ошибки”: Дочерняя клетка несет в себе одну или несколько хромосом, которые не гомологичны ни одной хромосоме родительского организма. Такие изменения называются мутациями. Может оказаться, что в одном или нескольких локусах измененной хромосомы находятся аллели, не встречавшиеся у родителя. Тогда говорят, что произошла генная мутация. Бывают случаи, когда у мутировавшей хромосомы локусы следуют не в естественном порядке, или же присутствуют участки “вырванные” из других, негомологичных хромосом. Возможны и другие отклонения. Например, отсутствие части локусов. В этом случае говорят о хромосомных мутациях. Ниже рассматриваются только генные мутации. Отметим, что генные мутации могут возникать спонтанно вследствие молекулярных изменений. Кроме того мутации индуцируются ультрофиолетовым, ренгеновским или радиоактивным излучением. Они могут происходить также в результате воздействия на организм химических веществ, называемых мутагенами (например, иприт).
Генные мутации оказывают на организм самые различные воздействия: от
едва заметного до летального. Вред, причиняемый организму мутациями, часто
зависит от конкретных условий. Например, у мухи дрозофилы существует класс
мутаций, называемых “температурочувствительными”. При температуре от ![]() до
до ![]() муху, гомозиготные по таким
мутациям, живут и размножаются более менее нормально. Однако, при температуре
около
муху, гомозиготные по таким
мутациям, живут и размножаются более менее нормально. Однако, при температуре
около ![]() эти мухи погибают, тогда как
мухи обычного типа продолжают функционировать нормально.
эти мухи погибают, тогда как
мухи обычного типа продолжают функционировать нормально.
Вновь возникающие мутации, как правило, вредны для организма. С одной стороны, мутации происходят независимо от того, приносят они организму вред или пользу. В то же время, аллели, существующие в популяции, уже подверглись естественному отбору. Если они поддерживаются в популяци со значительной частотой, то лишь потому, что повышают, или когда -то повышали приспособленность носителей этих аллелей по сравнения с носителями альтернативных аллелей. Только что возникающие мутации, как правило, уже встречались в истории популяции. Если они не поддерживаются в популяции со значительной частотой, то это означает, что они не приносят пользы своим обладателям.
Иногда, однако, новые мутации могут увеличивать приспособленность организмов. Например, если популяция осваивает новую территорию, или, если резко меняются внешние условия, предъявляющие популяции новые требования. В экстремальных условиях приспособленность организмов оказывается ниже оптимальной, и новые мутации могут оказаться полезными. Таким образом, результат мутаций для организмов зависит от условий обитания. Например, считается, что повышенное содержание меланина в кожном покрове (темная кожа) полезно для людей, населяющих тропическую Африку. Темная кожа лучше защищает от ультрофиолетового излучения. Наоборот, для жителей севера, где освещенность мала, светлая кожа способствует синтезу витамина D.
Вероятность того, что в гамете в конкретном локусе конкретной хромосомы
появился аллель, не встречавшийся у родителя, называется темпом мутирования
гена. Темп мутирования бактерий и других микроорганизмов обычно выше чем
многоклеточных организмов. Он весьма сильно варьируется от гена к гену и от
организма к организму. Для человека и других многоклеточных организмов
показано, что мутации (в отдельном локусе) возникают с частотой ![]() .
.
Пусть темп мутирования гена суть ![]() .
Все диплоидные организмы образуются от слияния двух гамет. Вероятность того,
что у данной особи в том или ином локусе возникает мутация суть
.
Все диплоидные организмы образуются от слияния двух гамет. Вероятность того,
что у данной особи в том или ином локусе возникает мутация суть ![]() , т.е. она приближенно
равна удвоенному значению темпа мутации. Таким образом, эта вероятность весьма
мала. Однако, вероятность того, что данная особь окажется носителем мутации,
возникшем где -либо в генном наборе, уже не столь мала. В генотипе человека
имеется порядка
, т.е. она приближенно
равна удвоенному значению темпа мутации. Таким образом, эта вероятность весьма
мала. Однако, вероятность того, что данная особь окажется носителем мутации,
возникшем где -либо в генном наборе, уже не столь мала. В генотипе человека
имеется порядка ![]() локусов.
Предположим что темп мутирования для генов человека
локусов.
Предположим что темп мутирования для генов человека ![]() .
Число мутаций распределено по биномиальному закону. Математическое ожидание
числа мутаций суть
.
Число мутаций распределено по биномиальному закону. Математическое ожидание
числа мутаций суть ![]() . Иными словами,
каждый человек в среднем имеет два аллеля, отсутствовуюших у родителей.
. Иными словами,
каждый человек в среднем имеет два аллеля, отсутствовуюших у родителей.
Возникает некоторое противоречие. С одной стороны в целом мутации
вредны. С другой стороны практически все люди являются носителями мутаций. В
связи с этим обсудим судьбу единичной мутации в модельной популяции, целиком
состоящей из особей генотипа ![]() . Пусть в
единственной гамете произошла мутация аллеля
. Пусть в
единственной гамете произошла мутация аллеля ![]() в
в
![]() . Тогда в нулевом поколении
появляется одна и только одна особь генотипа
. Тогда в нулевом поколении
появляется одна и только одна особь генотипа ![]() .
При скрещивании с особью генотипа
.
При скрещивании с особью генотипа ![]() получаем
получаем
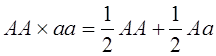 , т.е. каждый потомок этой
пары равновероятно относится к генотипам
, т.е. каждый потомок этой
пары равновероятно относится к генотипам ![]() и
и
![]() . Если появится только один
потомок, то вероятность утраты аллеля -мутанта
. Если появится только один
потомок, то вероятность утраты аллеля -мутанта ![]() будет
равна 0.5 (потомок принадлежит генотипу
будет
равна 0.5 (потомок принадлежит генотипу ![]() ).
Если в первом поколении появилось
).
Если в первом поколении появилось ![]() потомков,
то вероятность утраты аллеля
потомков,
то вероятность утраты аллеля ![]() суть
суть ![]() . Для расчета полной
вероятности потери аллеля
. Для расчета полной
вероятности потери аллеля ![]() в первом
поколении неоходимо знать вероятность появления
в первом
поколении неоходимо знать вероятность появления ![]() потомков.
Часто предполагают (это не бесспорно), что достаточно хорошим приближением для
распределения числа потомков является распределение Пуассона. Предположим, что
среднее число потомков на семью равно двум. Тогда вероятность появления
потомков.
Часто предполагают (это не бесспорно), что достаточно хорошим приближением для
распределения числа потомков является распределение Пуассона. Предположим, что
среднее число потомков на семью равно двум. Тогда вероятность появления ![]() потомков суть
потомков суть 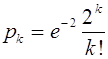 . Полная вероятность потери
аллеля мутанта в первом поколении будет равна
. Полная вероятность потери
аллеля мутанта в первом поколении будет равна
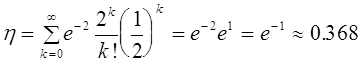 .
.
Если аллель ![]() не потерян в
первом поколении, то он может быть потерян во втором поколении. Вычислим
вероятность потери аллеля за два поколения. Пусть в результате скрещивания
особей
не потерян в
первом поколении, то он может быть потерян во втором поколении. Вычислим
вероятность потери аллеля за два поколения. Пусть в результате скрещивания
особей ![]() и
и ![]() в первом поколении
появилось
в первом поколении
появилось ![]() потомков. Вероятность того,
что
потомков. Вероятность того,
что ![]() потомков будут относиться к
генотипу
потомков будут относиться к
генотипу ![]() суть
суть 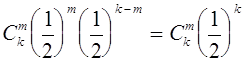 (биномиальное
распределение). Будем считать, что особи
(биномиальное
распределение). Будем считать, что особи ![]() первого
поколения скрещиваются только с особями генотипа
первого
поколения скрещиваются только с особями генотипа ![]() (генотип
(генотип
![]() редок). Вероятность того,
что ни одна из
редок). Вероятность того,
что ни одна из ![]() особей первого
поколения генотипа
особей первого
поколения генотипа ![]() не оставит
потомство, имеющее аллель
не оставит
потомство, имеющее аллель ![]() будет
равна
будет
равна ![]() , где, напомним,
, где, напомним, ![]() - вероятность этого явления
для одной особи. Если в первом поколении было
- вероятность этого явления
для одной особи. Если в первом поколении было ![]() потомков
от скрещивания особей
потомков
от скрещивания особей ![]() и
и ![]() нулевого поколения, то
вероятность потери аллеля
нулевого поколения, то
вероятность потери аллеля ![]() во втором
поколении равна
во втором
поколении равна
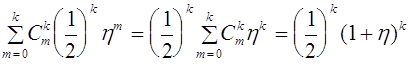 .
.
Наконец, получаем полную вероятность потери аллеля ![]() во втором поколении
(включая вероятность того, что он потерян уже в первом поколении):
во втором поколении
(включая вероятность того, что он потерян уже в первом поколении):
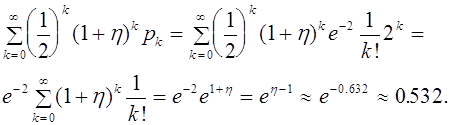
Итак, более половины мутаций будут потеряны потомками за два поколения, Можно рассчитать вероятность потери мутации и в последующих поколениях. Тенденция понятна. Большинство мутаций будет утеряно в течении нескольких поколений, даже, если некоторые из них благоприятны в борьбе за выживание. Приблизительно говоря, для вновь появившегося аллеля не столь опасна вероятность гибели (в модели возможность гибели не учитывалась). Гораздо страшнее потеряться при передаче в следуюшему поколению.
Давление повторных мутаций
Мы проследили за судьбой единичной мутации и убедились, что вероятность потери мутировавшего аллеля с ростом номера поколения растет. Однако, в каждом новом поколении вновь возникают мутации. Темп мутирования при постоянных условиях для каждого локуса из поколения в поколение остается достаточно стабильным.
Пусть ![]() - темп
мутирования, т.е. вероятность замены аллеля
- темп
мутирования, т.е. вероятность замены аллеля ![]() на
на
![]() в следующем поколении.
Обозначим через
в следующем поколении.
Обозначим через ![]() и
и ![]() соответственно частоты
аллелей
соответственно частоты
аллелей ![]() и
и![]() в
в ![]() -ом поколении. Тогда в
следующем поколении частота аллеля
-ом поколении. Тогда в
следующем поколении частота аллеля ![]() увеличивается
на
увеличивается
на ![]() за счет уменьшения частоты
аллеля
за счет уменьшения частоты
аллеля ![]() на
на ![]() :
:
![]() ,
, ![]() .
.
Из первого уравнения получаем ![]() .
Поскольку
.
Поскольку ![]() , то
, то ![]() . Вследствие малости
величины
. Вследствие малости
величины ![]() имеем
имеем ![]() и
и ![]() . При
. При ![]() частота
частота ![]() , т.е. ростом номера
поколения все аллели
, т.е. ростом номера
поколения все аллели ![]() превращаются в
превращаются в ![]() . Этот процесс чрезвычайно
медленный. Сделаем весьма естественное допущение, что
. Этот процесс чрезвычайно
медленный. Сделаем весьма естественное допущение, что ![]() . Тогда для снижения частоты
аллеля
. Тогда для снижения частоты
аллеля ![]() с 1 до 0.99 (аллель -мутант
встречается примерно у одной особи из ста) требуется 1000 поколений. Если бы
мутации были единственным процессом, обуславливающим эволюционные изменения в
популяции, то эволюция протекала бы невероятно медленно. Это основной урок,
который следует извлечь из рассмотренного примера.
с 1 до 0.99 (аллель -мутант
встречается примерно у одной особи из ста) требуется 1000 поколений. Если бы
мутации были единственным процессом, обуславливающим эволюционные изменения в
популяции, то эволюция протекала бы невероятно медленно. Это основной урок,
который следует извлечь из рассмотренного примера.
Мутации генов часто бывают обратимыми. Как только только аллель
становится довольно частым в популяции, следует учитывать следует учитывать
мутирование как к нему так и от него. Пусть ![]() -темп
мутирования аллеля
-темп
мутирования аллеля ![]() в
в ![]() . Темп обратного мутирования
обозначим через
. Темп обратного мутирования
обозначим через ![]() . Уравнения
эволюции имеют вид:
. Уравнения
эволюции имеют вид:
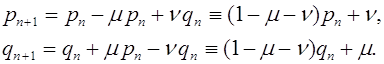
Состояние равновесия эволюционных уравнений:
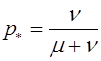 ,
, 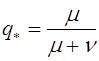 .
.
Оно устойчиво. Действительно
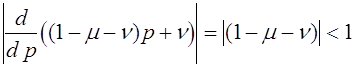 .
.
Осталось сослаться на приведенное выше утверждение об устойчивости
неподвижных точек одномерных отображений. Впрочем, это слишком сложно. Поступим
по другому. Введем новую переменную ![]() , или же
, или же
![]() . В результате подстановки
получим:
. В результате подстановки
получим:
![]() .
.
Отсюда следует, что ![]() и
и ![]() при
при ![]() . Приближенно
. Приближенно ![]() . Таким образом, скорость
сходимости к состоянию равновесия весьма не велика.
. Таким образом, скорость
сходимости к состоянию равновесия весьма не велика.
Взаимодействие отбора и мутаций
В природе одбор и мутации протекают одновременно. Имеет
смысл изучить их совместное действие. Рассмотрим однолокусную популяцию с
аллелями ![]() и
и ![]() . Предположим, что мутации
происходят в гаметах (в половых клетках родительских организмов). Темп
мутирования за одно поколение аллеля
. Предположим, что мутации
происходят в гаметах (в половых клетках родительских организмов). Темп
мутирования за одно поколение аллеля![]() в аллель
в аллель
![]() обозначим через
обозначим через ![]() . Считаем, что
. Считаем, что ![]() . Пусть
. Пусть ![]() и
и ![]() -частоты аллелей
-частоты аллелей ![]() и
и ![]() в
в ![]() -ом поколении в момент
появления его на свет. Относительные приспособленности генотипов
-ом поколении в момент
появления его на свет. Относительные приспособленности генотипов ![]() ,
, ![]() и
и ![]() обоэначим как
обоэначим как ![]() ,
, ![]() и
и ![]() соответственно. В
соответствии с (16) и (17) (уравнение для отбора в менделевской популяции)
эволюция для частоты аллеля
соответственно. В
соответствии с (16) и (17) (уравнение для отбора в менделевской популяции)
эволюция для частоты аллеля ![]() задается
одномерным отображением:
задается
одномерным отображением:
![]() ,
(24)
,
(24)
где
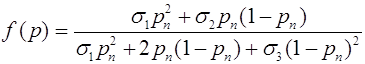 .
.
В правой части (24) слагаемое ![]() -
уменьшение частоты аллеля
-
уменьшение частоты аллеля ![]() за счет
мутирования в аллель
за счет
мутирования в аллель ![]() . Очевидно, для
частоты аллеля
. Очевидно, для
частоты аллеля ![]() имеем
имеем ![]() .
.
Выше было показано, что 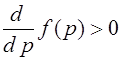 для
всех
для
всех ![]() . Поскольку параметр
. Поскольку параметр ![]() , правая часть отображения
(24) является также монотонно растущей функцией для
, правая часть отображения
(24) является также монотонно растущей функцией для ![]() . На основе этого факта выше
было доказано, что все траектории одномерного отображения стремятся к
состояниям равновесия.
. На основе этого факта выше
было доказано, что все траектории одномерного отображения стремятся к
состояниям равновесия.
Рассмотрим некоторые частные случаи. Пусть отбор
действует против особей рецессивного гомозиготного генотипа ![]() . Будем считать, что
относительные приспособленности генотипов
. Будем считать, что
относительные приспособленности генотипов ![]() и
и
![]() равны между собой и выше
относительной приспособленности генотипа
равны между собой и выше
относительной приспособленности генотипа ![]() .
Положим:
.
Положим: ![]() и
и ![]() . Отображение (24)
приобретает вид:
. Отображение (24)
приобретает вид:
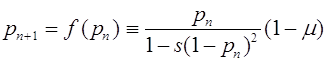 . (25)
. (25)
Его неподвижные точки суть ![]() и
и 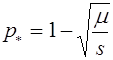 . Второе состояние
равновесия существует только в случае
. Второе состояние
равновесия существует только в случае ![]() .
Для малой окрестности нуля имеем:
.
Для малой окрестности нуля имеем:
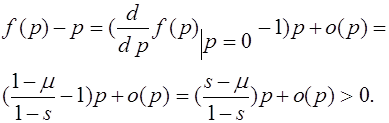
Поскольку на интервале ![]() нет
состояний равновесия, то
нет
состояний равновесия, то ![]() для
всех
для
всех ![]() . В результате, траектории с
начальным условием
. В результате, траектории с
начальным условием ![]() стремятся к
состоянию равновесия
стремятся к
состоянию равновесия ![]() , т.е.
, т.е. ![]() при
при ![]() . Далее,
. Далее, ![]() . Следовательно,
. Следовательно, ![]() для всех
для всех ![]() . Траектории с начальным
условием
. Траектории с начальным
условием ![]() также стремятся к этому
состоянию равновесия, которое оказывается глобально устойчивым. Напомним, что
устойчивое состояние равновесия, для которого частоты обоих аллелей ненулевые,
называется балансированным полиморфизмом. Выше было показано, что для
случая, когда отбор действует против рецессивных гамет и отсутствуют мутации,
полиморфизм невозможен (рецессивный аллель вытесняется из популяции). Если
рецессивный аллели
также стремятся к этому
состоянию равновесия, которое оказывается глобально устойчивым. Напомним, что
устойчивое состояние равновесия, для которого частоты обоих аллелей ненулевые,
называется балансированным полиморфизмом. Выше было показано, что для
случая, когда отбор действует против рецессивных гамет и отсутствуют мутации,
полиморфизм невозможен (рецессивный аллель вытесняется из популяции). Если
рецессивный аллели ![]() летальны
летальны ![]() , то значения равновесных
частот суть
, то значения равновесных
частот суть ![]() и
и ![]() . При достаточно типичном
темпе мутирования
. При достаточно типичном
темпе мутирования ![]() получаем
равновесную частоту рецессивного летального аллеля
получаем
равновесную частоту рецессивного летального аллеля ![]() .
Это достаточно высокая вероятность возникновения генетического заболевания ( в
среднем три особи на тысячу).
.
Это достаточно высокая вероятность возникновения генетического заболевания ( в
среднем три особи на тысячу).
Если ![]() (отбор
против рецессивных гомозигот менее интенсивен нежели мутации), то состояние
равновесия
(отбор
против рецессивных гомозигот менее интенсивен нежели мутации), то состояние
равновесия ![]() отсутствует и отображение
(25) имеет единственную неподвижную точку
отсутствует и отображение
(25) имеет единственную неподвижную точку ![]() ,
к которой, естественно, сходятся все траектории. Таким образом, несмотря на
лучшую приспособленность обладателей аллеля
,
к которой, естественно, сходятся все траектории. Таким образом, несмотря на
лучшую приспособленность обладателей аллеля ![]() ,
засчет мутаций происходит вытеснение этого аллеля.
,
засчет мутаций происходит вытеснение этого аллеля.
Рассмотрим теперь случай, когда гомозиготный геннотип ![]() имеет самую высокую относительную
приспособленность. Пусть
имеет самую высокую относительную
приспособленность. Пусть ![]() ,
, ![]() , где
, где ![]() . Преобразуем правую часть
уравнение эволюции (24). Последовательно получаем
. Преобразуем правую часть
уравнение эволюции (24). Последовательно получаем ![]() :
:
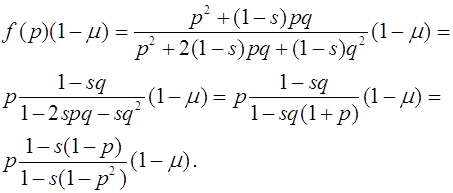
Далее,
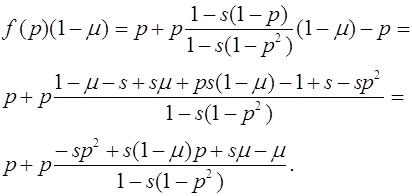
Тем самым, отображение (24) приобретает вид:
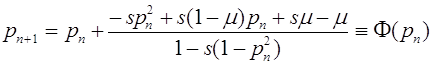 .
.
Одна из неподвижных точек отображения, очевидно, ![]() . Две другие определяются из
уравнения:
. Две другие определяются из
уравнения:
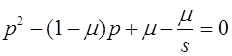 .
.
Получаем:
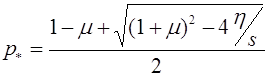 ,
, 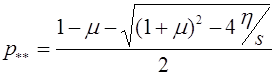 .
.
Оба корня существуют поскольку ![]() .Здесь
.Здесь
![]() . Поскольку
. Поскольку ![]() для
для ![]() , то знак разности
, то знак разности ![]() определяется знаком
квадратного трехчлена
определяется знаком
квадратного трехчлена ![]() . Если
. Если ![]() , то
, то ![]() . Если же
. Если же ![]() , то
, то ![]() . Наконец,
. Наконец, ![]() для
для ![]() . (См. Рисунок.)Тем самым,
при начальной точке
. (См. Рисунок.)Тем самым,
при начальной точке ![]() траектории
траектории ![]() при
при ![]() . Состояние полиморфизма
. Состояние полиморфизма ![]() ,
, ![]() устойчиво (полиморфизм
балансирован). Соответственно, состояние равновесия
устойчиво (полиморфизм
балансирован). Соответственно, состояние равновесия ![]() неустойчиво.
Если начальная точка
неустойчиво.
Если начальная точка![]() , то
соответствующая траектория стремится к нулю. Однако, нужно заметить, что здесь
мы выходим за рамки применимости модели. При больших концентрациях аллеля
, то
соответствующая траектория стремится к нулю. Однако, нужно заметить, что здесь
мы выходим за рамки применимости модели. При больших концентрациях аллеля ![]() нужно учитывать мутации от
аллелей
нужно учитывать мутации от
аллелей ![]() к аллелям
к аллелям ![]() .
.
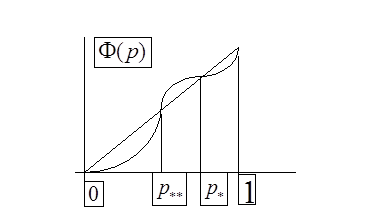
Миграции
Миграции, или поток генов возникают, когда особи одной популяции перемещаются в другую и скрещиваются с членами второй популяции. Поток генов не меняют частоты аллелей у вида в целом. Однако, частоты могут меняться в локальных популяциях, если исходные частоты различны у старожилов и пришельцев.
Рассмотрим простейшую модель, описывающую локальную
популяцию, в которую с определенной частотой мигрируют особи из окружающей
популяции и скрещиваются со старожилами. Предположим, что частота аллеля ![]() в окружающей популяции
постоянна и равна
в окружающей популяции
постоянна и равна ![]() . Пусть
. Пусть ![]() -вероятность обнаружения
пришельца среди особей текущего поколения (доля мигрантов). Эта вероятность
характеризует интенсивность миграции. Считаем, что доля пришельцев для всех
поколений одна и та же.
-вероятность обнаружения
пришельца среди особей текущего поколения (доля мигрантов). Эта вероятность
характеризует интенсивность миграции. Считаем, что доля пришельцев для всех
поколений одна и та же.
Обозначим частоту аллеля ![]() для
локальной популяции через
для
локальной популяции через ![]() . Тогда
частота для следующего поколения суть:
. Тогда
частота для следующего поколения суть:
![]() .
.
Здесь ![]() -вероятность
того, что гамета
-вероятность
того, что гамета ![]() -ого поколения
является старожилом и обладает аллелем
-ого поколения
является старожилом и обладает аллелем ![]() .
Соответственно,
.
Соответственно, ![]() -вероятность
того, что гамета является пришельцем и имеет аллель
-вероятность
того, что гамета является пришельцем и имеет аллель ![]() .
Положим:
.
Положим: ![]() . В результате получим:
. В результате получим:
![]() ,
,
![]() .
.
Поскольку ![]() , то то
с ростом номера поколения
, то то
с ростом номера поколения ![]() и
и ![]() . Частота аллеля
. Частота аллеля ![]() в локальной популяции
уравниваетсяс его частотой во внешней популяции. Полученную формулу можно
использовать для оценки интенсивности потока генов. Рассмотрим пример.
в локальной популяции
уравниваетсяс его частотой во внешней популяции. Полученную формулу можно
использовать для оценки интенсивности потока генов. Рассмотрим пример.
В США потомство от смешанных браков между белыми и
темнокожими принято относить к темнокожему населению. Следовательно, смешанные
браки можно рассматривать как поток генов из белой в темнокожую популяцию.
Частота аллеля ![]() , контролирующего
резус фактор, у белого населения США составляет
, контролирующего
резус фактор, у белого населения США составляет ![]() .
В африканских племенах, от которых происходит современное темнокожее население
США, частота этого аллеля
.
В африканских племенах, от которых происходит современное темнокожее население
США, частота этого аллеля ![]() . Предки
современных темнокожих США были вывезены из Африки примерно
. Предки
современных темнокожих США были вывезены из Африки примерно ![]() лет назад (около
лет назад (около ![]() поколений), следовательно
на данный момент
поколений), следовательно
на данный момент ![]() . Частота аллеля
. Частота аллеля ![]() у современного темнокожего
населения США
у современного темнокожего
населения США ![]() . Получаем:
. Получаем:
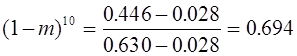 .
.
![]() ,
,
![]() .
.
Число ![]() -вероятность
того, что данный аллель не являлся мигрантом ни в одном из десяти
предшествующих поколений. Тем самым, современное темнокожее население США
наследовало около
-вероятность
того, что данный аллель не являлся мигрантом ни в одном из десяти
предшествующих поколений. Тем самым, современное темнокожее население США
наследовало около ![]() генов от своих
африканских предков, а
генов от своих
африканских предков, а ![]() генов получило от
белых предков. Неудивительно, что темнокожие американцы по внешнему виду
существенно отличаются от африканцев. Отметим, что число
генов получило от
белых предков. Неудивительно, что темнокожие американцы по внешнему виду
существенно отличаются от африканцев. Отметим, что число ![]() примерно соответствует
проценту смешанных браков.
примерно соответствует
проценту смешанных браков.
Приведенные вкладки носят приближенный характер. Если в аналогичных расчетах использовать частоты других аллелей, то получатся несколько другие результаты. Кроме того, интенсивность потока генов в разных регионах США различна. Однако, тенденция к выравниванию частот аллелей между темнокожим и белым населением сохраняется.
Рассмотрим островную модель Райта. Эта модель
учитывает как миграции, так и процессы отбора. Она описывает популяцию аллелей ![]() и
и ![]() , которая состоит из
, которая состоит из ![]() субпопуляций. Обозначим
через
субпопуляций. Обозначим
через ![]() , где
, где ![]() , доли субпопуляций
(вероятности того, что что выбранный аллель принадлежит
, доли субпопуляций
(вероятности того, что что выбранный аллель принадлежит ![]() -ой популяции). Будем
считать, что эти доли из поколения в поколение неизменны. Субпопуляции связаны
между собой меграционными процессами. Непосредственно после появления на свет
нового поколения из каждой субполяции с вероятностью
-ой популяции). Будем
считать, что эти доли из поколения в поколение неизменны. Субпопуляции связаны
между собой меграционными процессами. Непосредственно после появления на свет
нового поколения из каждой субполяции с вероятностью ![]() аллели (их носители)
совершают путешествие в некий “общий котел” аллелей (внешний мир). Считаем, что
вероятность
аллели (их носители)
совершают путешествие в некий “общий котел” аллелей (внешний мир). Считаем, что
вероятность ![]() миграции для всех
субпопуляций одна и та же. В “общем котле” аллели перемешиваются, “забывают” о
своем “географическом” происхождении и мигрируют в субпопуляции. Пусть
вероятность обнаружить вернувшихся путешественников (доля мигрантов) для всех
субпопуляций одна и та же и равна
миграции для всех
субпопуляций одна и та же. В “общем котле” аллели перемешиваются, “забывают” о
своем “географическом” происхождении и мигрируют в субпопуляции. Пусть
вероятность обнаружить вернувшихся путешественников (доля мигрантов) для всех
субпопуляций одна и та же и равна ![]() , т.е.
совпадает с вероятностью исхода юных аллелй из субпопуляций. Далее, в
субпопуляциях начинается процесс отбора. Он происходит на уровне аллелей (для
генотипов имеет место отбор геометрического типа). Пусть
, т.е.
совпадает с вероятностью исхода юных аллелй из субпопуляций. Далее, в
субпопуляциях начинается процесс отбора. Он происходит на уровне аллелей (для
генотипов имеет место отбор геометрического типа). Пусть ![]() и
и ![]() -вероятности того, что в
-вероятности того, что в ![]() -ой субпопуляции
соответственно аллели
-ой субпопуляции
соответственно аллели ![]() и
и ![]() доживают до этапа
размножения (эти числа также называются коэффициентами отбора).
доживают до этапа
размножения (эти числа также называются коэффициентами отбора).
Получим эволюционные уравнения. Пусть ![]() и
и ![]()
![]() -частоты
аллелей
-частоты
аллелей ![]() и
и ![]() в
в ![]() -ой субпопуляции в момент
появления на свет
-ой субпопуляции в момент
появления на свет ![]() -ого поколения.
Средние частоты аллелей
-ого поколения.
Средние частоты аллелей ![]() и
и ![]() во всей популяции в момент
рождения
во всей популяции в момент
рождения ![]() -ого поколения суть:
-ого поколения суть:
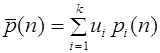 ,
,
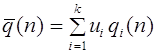 . (26)
. (26)
Эти же числа -частоты аллелей в “общем котле”. Для
произвольной ![]() -ой субпопуляции после
завершения миграционных процессов имеют место следующие частоты аллелей
-ой субпопуляции после
завершения миграционных процессов имеют место следующие частоты аллелей ![]() и
и ![]() :
:
![]() ,
, ![]() .
.
Полная вероятность того, что после завершения миграции в ![]() -ой субпопуляции аллель
-ой субпопуляции аллель ![]() -ого поколения доживет до
этапа размножения определяется следующим образом:
-ого поколения доживет до
этапа размножения определяется следующим образом:
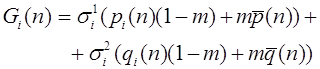 .
(27)
.
(27)
Используя формулу Бейеса (теорема гипотез) получим частоты ![]() и
и ![]() в
в ![]() -ом поколении для
-ом поколении для ![]() -ой субпопуляции к моменту
начала этапа размножения:
-ой субпопуляции к моменту
начала этапа размножения:
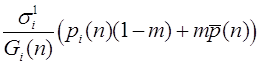 ,
, 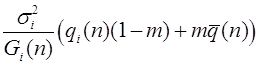 .
.
Такие же частоты имеют гаметы ![]() -ого
поколения и вновь появившиеся аллели
-ого
поколения и вновь появившиеся аллели ![]() и
и ![]() следующего
следующего ![]() -ого поколения. Тем самым,
получаем эволюцинные уравнения для частот:
-ого поколения. Тем самым,
получаем эволюцинные уравнения для частот:
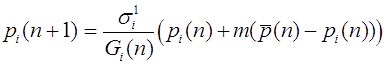 ,
(28)
,
(28)
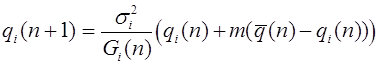 .
(29)
.
(29)
где ![]() -номера
субпопуляций. В (28), (29) средние частоты
-номера
субпопуляций. В (28), (29) средние частоты ![]() и
и
![]() заданы формулами (26), а
нормировочные коэффициенты
заданы формулами (26), а
нормировочные коэффициенты ![]() -формулами
(27). Отметим, что отображение (28), (29) не меняет вид после замены
-формулами
(27). Отметим, что отображение (28), (29) не меняет вид после замены ![]() и
и ![]() . В связи с этим положим
. В связи с этим положим ![]() и
и ![]() , где
, где ![]() . Если
. Если ![]() , то аллель
, то аллель ![]() имеет преимущество в борьбе
за существование перед аллелем
имеет преимущество в борьбе
за существование перед аллелем ![]() . Если же
. Если же
![]() , то преимущество - за
аллелем
, то преимущество - за
аллелем ![]() . Коэффициент
. Коэффициент ![]() легко преобразовать к виду:
легко преобразовать к виду:
![]() .
.
В результате формулы (28) приобретают вид:
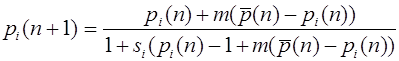
![]() , (30)
, (30)
Пусть во всех субпопуляциях отбор не происходит, т.е. ![]() . Используя (30) для средней
частоты аллеля
. Используя (30) для средней
частоты аллеля ![]() получаем:
получаем:
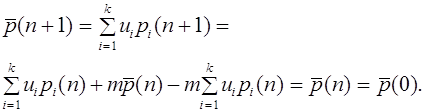
Средние частоты аллелей сохраняются. Из (30) получаем, что с
ростом номера поколения частоты ![]() .
Результат естественен: миграция выравнивает частоты.
.
Результат естественен: миграция выравнивает частоты.
Предположим, что во всех субпопуляциях отбор действует
против аллеля ![]() , т.е.
, т.е. ![]() . Предположим, что в
. Предположим, что в ![]() -ом поколении хотя бы для
одной субпопуляции частота аллеля
-ом поколении хотя бы для
одной субпопуляции частота аллеля ![]() меньше
единицы. Очевидно, что и средняя частота аллеля
меньше
единицы. Очевидно, что и средняя частота аллеля ![]() .
Тогда для всех субпопуляций получаем:
.
Тогда для всех субпопуляций получаем: ![]() .
В этом случае из (30) следует, что
.
В этом случае из (30) следует, что ![]() . Для
средней частоты выполнено неравенство
. Для
средней частоты выполнено неравенство ![]() ,
которое является строгим, пока по крайней мере в одной субпопуляции частота
аллеля
,
которое является строгим, пока по крайней мере в одной субпопуляции частота
аллеля ![]() не равна единице.
Последовательность
не равна единице.
Последовательность ![]() монотонно растет.
Она ограничена, а, следовательно, имеет предел. В предельной точке приращения
нет, а это возможно только, если для всех субпопуляций
монотонно растет.
Она ограничена, а, следовательно, имеет предел. В предельной точке приращения
нет, а это возможно только, если для всех субпопуляций ![]() . Тем самым, происходит
повсеместное вытеснение аллеля
. Тем самым, происходит
повсеместное вытеснение аллеля ![]() . В
случае, когда отбор действует против аллелей
. В
случае, когда отбор действует против аллелей ![]() (т.е.
(т.е.
![]() ), совершенно аналогичные
рассуждения показывают, что из популяции вытесняется аллель
), совершенно аналогичные
рассуждения показывают, что из популяции вытесняется аллель ![]() .
.
Направление отбора в разных субпопуляциях может быть
различным -числа ![]() имеют разные знаки.
В этом случае проверка сходимости итерационного процесса (30) представляет
собой не простую задачу. Для равновесных частот
имеют разные знаки.
В этом случае проверка сходимости итерационного процесса (30) представляет
собой не простую задачу. Для равновесных частот ![]() и
и
![]() ( неподвижных точек
отображения) получаем систему связанных между собой уравнений:
( неподвижных точек
отображения) получаем систему связанных между собой уравнений:
![]() .
(31)
.
(31)
Рассмотрим два частных случая. Пусть параметры ![]() малы. Смысл допущения
заключается в том, что влияние миграции более существенно, чем процесс отбора.
Уравнения (31) перепишем в виде:
малы. Смысл допущения
заключается в том, что влияние миграции более существенно, чем процесс отбора.
Уравнения (31) перепишем в виде:
![]() .
(32)
.
(32)
Отбрасывая малые слагаемые, приближенно получим: либо ![]() , либо
, либо ![]() . Второй вариант невозможен
т.к.
. Второй вариант невозможен
т.к. ![]() . Из (32) с точностью до
слагаемых порядка
. Из (32) с точностью до
слагаемых порядка ![]() получаем:
получаем:
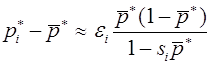 .
.
Поскольку ![]() ,
получаем, что либо
,
получаем, что либо ![]() , либо
, либо ![]() , или же
, или же ![]() удовлетворяет соотношению:
удовлетворяет соотношению:
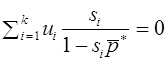 .
(33)
.
(33)
Заметим, что правая часть уравнения -монотонно растущая
функция от ![]() . Действительно, для тех
. Действительно, для тех ![]() , где
, где ![]() , сдагаемые
, сдагаемые ![]() монотонно убывают.
Наоборот, если
монотонно убывают.
Наоборот, если ![]() , то
соответствующие слагаемые монотонно растут. Пусть
, то
соответствующие слагаемые монотонно растут. Пусть ![]() ,
т.е. отбор интегрально действует против аллелей
,
т.е. отбор интегрально действует против аллелей ![]() .
Тогда при
.
Тогда при ![]() правая часть уравненния
положительна. Она положительна при всех
правая часть уравненния
положительна. Она положительна при всех ![]() ,
и уравнение (33) не имеет корней для
,
и уравнение (33) не имеет корней для ![]() . Если же
. Если же
![]() , т.е. отбор интегрально
действует против аллелей
, т.е. отбор интегрально
действует против аллелей ![]() , то
зеркальные рассуждения показывают, что уравнение также не может иметь состояний
равновесия. Тем самым, при интенсивной миграции один из аллелей
, то
зеркальные рассуждения показывают, что уравнение также не может иметь состояний
равновесия. Тем самым, при интенсивной миграции один из аллелей ![]() , или
, или ![]() вытесняется из популяции.
Какой конкретно аллель вытесняется, определяется знаком величины
вытесняется из популяции.
Какой конкретно аллель вытесняется, определяется знаком величины ![]() (если она положительна, то
аллели
(если она положительна, то
аллели ![]() имеют преимущество, и,
наоборот, если она отрицательна, то преимущество принадлежит аллелям
имеют преимущество, и,
наоборот, если она отрицательна, то преимущество принадлежит аллелям ![]() ). Прогнозы модели полностью
согласуются с биологическим смыслом.
). Прогнозы модели полностью
согласуются с биологическим смыслом.
Пусть теперь ![]() .
Перепишем уравнения (31) в виде:
.
Перепишем уравнения (31) в виде:
![]() .
.
Каждое из имеет два корня:
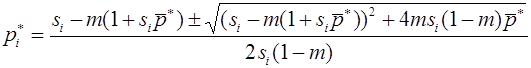 .
.
Обратим внимание, что полученные формулы не задают в явном
виде решение системы (31), поскольку в правых частях фигурирует средняя
частота ![]() , которая сама выражается
через
, которая сама выражается
через ![]() . Упростим формулу для
корней. Деля числитель и знаменатель дроби на
. Упростим формулу для
корней. Деля числитель и знаменатель дроби на ![]() и
пренебрегая слагаемыми порядка
и
пренебрегая слагаемыми порядка ![]() и
и ![]() по отношению к слагаемым
порядка
по отношению к слагаемым
порядка ![]() , последовательно получим:
, последовательно получим:
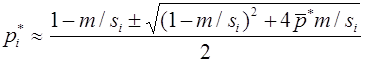 ,
,
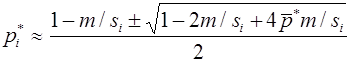 ,
,
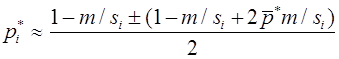 .
.
Здесь использовано то, что ![]() для
для
![]() . Для
. Для ![]() получаем:
получаем: ![]() . В свою очередь, для
. В свою очередь, для ![]() получаем:
получаем: ![]() . Найдем среднюю частоту
аллеля
. Найдем среднюю частоту
аллеля ![]() . Пусть
. Пусть ![]() для
для ![]() и
и ![]() для
для ![]() . Тогда, усредняя частоты в
субпопуляциях, получим:
. Тогда, усредняя частоты в
субпопуляциях, получим:
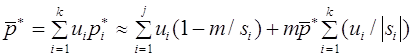 .
.
Отсюда следует, что
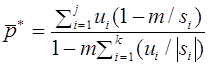 .
.
Средняя частота аллеля ![]() найдена.
Тем самым, найдены и частоты аллелей
найдена.
Тем самым, найдены и частоты аллелей ![]() в
субпопуляциях. В тех субпопуляциях, где отбор действует против аллелей
в
субпопуляциях. В тех субпопуляциях, где отбор действует против аллелей ![]() , частоты аллелей
, частоты аллелей ![]() близки к единице. Наоборот,
если отбор действует против аллелей
близки к единице. Наоборот,
если отбор действует против аллелей ![]() , их
частоты близки к нулю. Предсказания модели полностью согласуются с
биологическим смыслом.
, их
частоты близки к нулю. Предсказания модели полностью согласуются с
биологическим смыслом.
Дрейф генов
Дрейф генов -это случайные отклонения частот аллелей от теоретически ожидаемых, возникающие в результате недостаточного объема выборки. Такие явления часто называют ошибками выборки. Дрейф генов постоянно происходит в популяциях, поскольку их численность всегда конечна. Дополнительно заметим, что правильное представление о численности популяции дает не общее число особей, а число особей дающих начало следующему поколению. Действительно, только они дают вклад в генофонд следующего поколения.
Будем рассуждать в терминах
аллелей, не переходя к генотипам. Рассмотрим популяцию аллелей ![]() и
и ![]() . Пусть априорно их частоты
суть
. Пусть априорно их частоты
суть ![]() и
и ![]() . Случайным образом
сформируем выборку из
. Случайным образом
сформируем выборку из ![]() аллелей, которые
оставят потомство. Пусть
аллелей, которые
оставят потомство. Пусть ![]() -число
аллелей
-число
аллелей ![]() в выборке. Согласно теореме
Муавра -Лапласа вероятность
в выборке. Согласно теореме
Муавра -Лапласа вероятность ![]() события
события ![]() , где
, где ![]() , стремится при
, стремится при ![]() к числу
к числу ![]() . Здесь
. Здесь ![]() -нормальное распределение.
В частности, если
-нормальное распределение.
В частности, если ![]() , то
, то ![]() . Для эмпирической частоты
. Для эмпирической частоты ![]() аллеля
аллеля ![]() в выборке получаем оценку:
в выборке получаем оценку: ![]() , которая выполнена с
вероятностью
, которая выполнена с
вероятностью ![]() . Поскольку
. Поскольку ![]() , то
, то ![]() . Чем длиннее выборка, тем
эмпирическая частота ближе к априорной. Например, при
. Чем длиннее выборка, тем
эмпирическая частота ближе к априорной. Например, при ![]() получаем
получаем ![]() . Наоборот, при
. Наоборот, при ![]() эмпирическая частота аллеля
эмпирическая частота аллеля
![]() может принимать лишь одно
из трех значений
может принимать лишь одно
из трех значений ![]() , т.е.
эмпирическая частота в общем случае далека от априорной.
, т.е.
эмпирическая частота в общем случае далека от априорной.
Рассмотрим следующую
модельную ситуацию. Пусть для родителей, давших жизнь первому поколению, аллели
![]() и
и ![]() наблюдались с априорными
частотами
наблюдались с априорными
частотами ![]() и
и ![]() . Начиная с нулевого
поколения случайным образом формируется выборка из
. Начиная с нулевого
поколения случайным образом формируется выборка из ![]() аллелей,
которые дают начало следующему поколению. Выборку назовем эффективной
популяцией, а ее длину - эффективной численностью. Будем считать, что из
поколения в поколение эффективная численность
аллелей,
которые дают начало следующему поколению. Выборку назовем эффективной
популяцией, а ее длину - эффективной численностью. Будем считать, что из
поколения в поколение эффективная численность ![]() неизменна.
Допустим еще, в момент появления на свет нового поколения общая численность
популяции становится значительно больше
неизменна.
Допустим еще, в момент появления на свет нового поколения общая численность
популяции становится значительно больше ![]() .
При этом частоты аллелей в новом поколении (до формирования эффективной
популяции) совпадают с частотами эффективной популяции предыдущего поколения.
.
При этом частоты аллелей в новом поколении (до формирования эффективной
популяции) совпадают с частотами эффективной популяции предыдущего поколения.
Будем говорить, что
эффективная популяция находится в состоянии ![]() ,
если она содержит ровно
,
если она содержит ровно ![]() аллелей
аллелей ![]() . Для состояния
. Для состояния ![]() частота аллелей
частота аллелей ![]() а эффективной популяции суть
а эффективной популяции суть
![]() . В любом поколении эффективная
популяция находится в одном из
. В любом поколении эффективная
популяция находится в одном из ![]() -ом
состояний
-ом
состояний ![]() . Рассмотрим эффективную
популяцию
. Рассмотрим эффективную
популяцию ![]() -ого поколения. Пусть она
находится в
-ого поколения. Пусть она
находится в ![]() -ом состоянии. Вероятность
того, что в следующем
-ом состоянии. Вероятность
того, что в следующем ![]() -ом поколении
эффективная популяция будет находиться в состоянии
-ом поколении
эффективная популяция будет находиться в состоянии ![]()
![]() суть
суть
![]() . (34)
. (34)
Обратим внимание, что ![]() и
и ![]() для всех
для всех ![]() , а также
, а также ![]() и
и ![]() для всех
для всех ![]() . Таким образом, если в
. Таким образом, если в ![]() -ом поколении популяция
оказывается в состояниях
-ом поколении популяция
оказывается в состояниях ![]() или
или ![]() , то в дальнейшем она
остается в эти состояниях. Пусть эффективная популяция
, то в дальнейшем она
остается в эти состояниях. Пусть эффективная популяция ![]() -ого поколения находится в
состояниях
-ого поколения находится в
состояниях ![]() с вероятностями
с вероятностями ![]() . Используя формулу полной
вероятности, получаем вероятности
. Используя формулу полной
вероятности, получаем вероятности
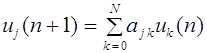 (35)
(35)
того, что эффективная популяция
![]() -ого поколения окажется в
состоянии
-ого поколения окажется в
состоянии ![]()
![]() .
Введем последовательность векторов
.
Введем последовательность векторов ![]() вероятностей
состояний эффективных популяций последовательных поколений и матрицу
вероятностей
состояний эффективных популяций последовательных поколений и матрицу ![]() . Тогда сотношения (35)
перепишутся в виде:
. Тогда сотношения (35)
перепишутся в виде:
![]() .
(36)
.
(36)
Оказалось, что рассматриваемая
система обладает следующим свойством. В любой дискретный момент времени она
может находиться в одном из ![]() -ом
состояний. Если в
-ом
состояний. Если в ![]() -ый дискретный момент
времени для нее известны вероятности нахождения в состояниях
-ый дискретный момент
времени для нее известны вероятности нахождения в состояниях ![]() , то однозначно вычисляются
вероятности обнаружить систему в этих состояниях в следующий момент времени.
Такие системы называются цепями Маркова. Матрица
, то однозначно вычисляются
вероятности обнаружить систему в этих состояниях в следующий момент времени.
Такие системы называются цепями Маркова. Матрица ![]() называется
матрицей переходных вероятностей.
называется
матрицей переходных вероятностей.
Как уже отмечалось, из формул
(34) для элементов матрицы ![]() следует,
что
следует,
что ![]() и
и ![]() . Рассматривая первую и
последнюю строки уравнений (36) получаем:
. Рассматривая первую и
последнюю строки уравнений (36) получаем:
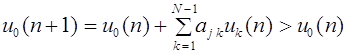 ,
,
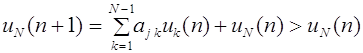 .
.
Эти неравенства строгие, пока
по крайней мере одно из чисел ![]() для
для ![]() . Тем самым,
последовательности
. Тем самым,
последовательности ![]() и
и ![]() монотонно растут. Поскольку
они ограничены, то имеют пределы:
монотонно растут. Поскольку
они ограничены, то имеют пределы: ![]() и
и ![]() при
при ![]() . В предельной точке
приращения нет, поэтому
. В предельной точке
приращения нет, поэтому ![]() для
для ![]() . Полученные результаты
означают, что в пределе в популяции остается либо аллель
. Полученные результаты
означают, что в пределе в популяции остается либо аллель ![]() , либо аллель
, либо аллель ![]() . Действительно, вероятность
события, что в популяции присутствуют оба аллеля равна нулю.
. Действительно, вероятность
события, что в популяции присутствуют оба аллеля равна нулю.
Вычислим значения ![]() и
и ![]() . Рассмотрим математическое
ожидание числа аллелей
. Рассмотрим математическое
ожидание числа аллелей ![]() в
в ![]() -ом эффективном поколении:
-ом эффективном поколении:
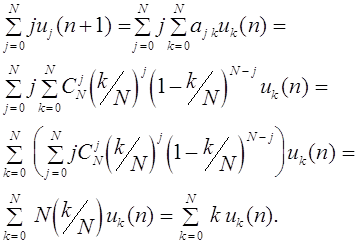
Таким образом, имеет место важнейшее соотношение для математического ожидания:
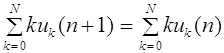 , (37)
, (37)
Отметим, что цепи Маркова, для которых выполнено данное соотношение , называются мартингалами. (Совершенно наивно интерпретировать (37), как то, что в среднем число аллелей сохраняется, т.к. один из аллелей вытесняется из популяции.)
Напомним, что для родителей,
давших начало нулевому поколению, аллели ![]() наблюдались
с априорной частотой
наблюдались
с априорной частотой ![]() . Следовательно,
математическое ожидание числа аллелей
. Следовательно,
математическое ожидание числа аллелей ![]() в
нулевом поколении суть
в
нулевом поколении суть ![]() . В предельном
состоянии математическое ожидание равно
. В предельном
состоянии математическое ожидание равно ![]() .
В результате получает вероятность
.
В результате получает вероятность ![]() события,
что из популяции будет вытеснен аллель
события,
что из популяции будет вытеснен аллель ![]() и,
соответственно, будет фиксирован аллель
и,
соответственно, будет фиксирован аллель ![]() .
.
Сделаем следующее замечание.
Пусть эффективная популяция нулевого поколения оказалась в состоянии ![]() , т.е. число аллелей
, т.е. число аллелей ![]() равно
равно ![]() . Тогда вероятность фиксации
аллеля
. Тогда вероятность фиксации
аллеля ![]() будет равна
будет равна ![]() . Таким образом, результаты
опыта позволяют уточнить априорную вероятность.
. Таким образом, результаты
опыта позволяют уточнить априорную вероятность.
Можно вычислить
математическое ожидание числа поколений, по прошествии которого один из аллелей
будет вытеснен из популяции. Оказывается, что это число ![]() задается формулой:
задается формулой:
![]() ,
,
где ![]() -априорная
частота аллеля
-априорная
частота аллеля ![]() у родителей,
давших начало нулевому поколению.
у родителей,
давших начало нулевому поколению.
Кумулятивные эффекты, или
эффекты накопления изменений в процессе дрейфа генов изучались экспериментально.
Питер Ф. Бьюри работал со 107 изолированными популяциями мух -дрозофил. В
каждой из них случайным образом отбиралось 8 самцов и 8 самок, которые давали
начало следующему поколению. Тем самым, эффективная численность популяции
составляла 16 особей, или же 32 аллеля. В начале эксперимента все особи были
гетерозиготны, т.е. априорные частоты аллелей были равны 0.5. Фиксация аллеля в
одной из популяций впервые произошла в четвертом поколении. Число популяций с
фиксированными аллелями постепенно расло на протяжении 19 поколений. Затем
эксперимент был прекращен. В 19 -ом поколении в 30 популяциях был фиксирован
один аллель, а 28 популяциях -другой. Если бы эксперимент продолжался дальше,
то в конце концов аллели были бы фиксированы во всех популяциях. Для обоих
аллелей число популяций, в которых они фиксированы, было бы одинаковым.
Отметим, что математическое ожидание числа поколений, по прошествии которого
один из аллелей фиксируется, для данного случая суть ![]() .
.
Если популяция многочисленна, то фактор дрейфа генов оказывает весьма незначительное влияние на частоты аллелей по сравнению с процессами отбора, мутации и миграции. Для маллых популяций, наоборот, дрейф генов существенен.
Предельный случай дрейфа генов возникновение новой популяции, первоначально состоявшей лишь из нескольких особей. Такой процесс Эрнст Майр назвал эффектом основателя. Популяции многих видов, обитающих на океанических островах, в настоящее насчитывают миллионы особей. Однако они происходят от нескольких, случайно попавших туда особей. В результате ошибок выборки частоты аллелей у основателей новой популяции могут существенно отличаться от частот аллелей в популяции, из которой произошли основатели. Это может наложить отпечаток на дальнейшую эволюцию.
Случайные изменения частот аллелей возникают также в случае, если популяция в своем развитии проходит “бутылочное горлышко”. Когда природные условия существования становятся неблагоприятными, численность популяции резко сокращается. В дальнейшем популяция может восстановить свою численность. Во время прохождения “бутылочного горлышка” частоты аллелей могут сильно измениться вследствие дрейфа. В дальнейшем эти изменения сохраняются на протяжении поколений. Естественно, особенно они заметны, если популяция находится в изоляции, т.е. отсутствует миграция генов извне. Известны сообщества такого рода в человеческом обществе.
Часть 2 Математические модели нейронных систем
Изучение нейронных систем -одно из самых романтических направлений научных исследований, поскольку нейронные системы присущи как человеку, так и животным. Самая совершенная интеллектуальная система -человеческий мозг. Никакой компьютер в настоящее время не может воспроизвести ее феномен. Более того, даже поведение таких относительно простых организмов, как кальмары, в настоящее время в полной мере невозможно смоделировать на компьютере. Законы функционирования отдельных элементов нервной системы в целом не плохо изучены. Однако, законы функционирования ассоциаций нельзя свести законам поведения отдельных элементов. На самом деле об эффектах, обусловленных коллективным поведением нейронных популяций, известно мало. Понятны некоторые самые общие принципы. Например, нейронные системы способны адаптироваться к меняющимся условиям, т.е. им не нужны жесткие программы. Одновремено, последние, хотя бы в форме рефлексов, присутствуют в нервной системе. Экспериментальное изучение эффектов коллективного поведения нейронных систем затруднено. Эти системы слишком сложно устроены. Так в мозге человека и животных каждый нейрон находится под воздействием тысяч других нейронов и, соответственно, влияет на тысячи нейронов. Всего же по современным оценкам в мозге порядка миллиарда нейронов. Огромное значение имеет математическое моделирование, как метод косвенного исследования. Оно помогает понять, какие процессы могут происходить в нейронных популяциях. Затем уже можно пытаться обнаружить соответствующие явления экспериментально. Модели различаются в зависимости от целей моделирования. Некоторые модели достаточно адекватно в деталях описывают поведение отдельных нейронов и помогают понять закономерности их функционирования. Они же являются базовыми для моделей малых нейронных популяций. Для описания больших популяций используют упрощенные модели нейронов. Упор делается на изучение эффектов коллективного поведения. Результаты моделирования используются как в нейрофизиологии, так и в технике. Уже сейчас выпускаются нейронные платы. Пока их возможности не велики. Они используются, например, в обработке изображений, а также при решении некоторых экономических задач. Следует отметить, что сейчас все задачи, которые можно решить с помощью нейронных плат, в принципе можно решить и с помощью обычного компьютера. Однако, нейронные платы увеличивают быстродействие. Перспективным считается направление, связанное с использованием нейронной техники для проведения вычислений. Ряд вычислений на нейроподобных системах может проводиться нетрадиционным способом -путем имитации явлений.
Возбудимые системы
Нервная клетка, или нейрон является структурной единицей нервной системы живых организмов. Индивидуальные границы нейрона, как и любой другой клетки, определяются клеточной мембраной. В любой клетке существует разность потенциалов между содержимым клетки -цитоплазмой и внеклеточной средой. Мембрана поляризована. Ее внутренняя поверхность заряжена отрицательно по отношению к внешней. Разность потенциалов называют мембранным потенциалом. Его величина составляет несколько десятков милливольт. Причина возникновения мембранного потенциала -неравенство концентраций ионов в цитоплазме и в тканевой жидкости. Это обусловлено тем, что клеточные мембраны обладают избирательной проницаемостью для различных ионов.
Живые организмы, все клетки и, в частности, нейроны обладают раздражимостью -способностью реагировать на различного рода воздействия. Реакции насят сложный, комплексный характер, но всегда сопровождаются изменением электрического заряда мембраны. Воздействия, вызывающие реакции, называются раздражителями, или стимулами. Хотя живые организмы состоят из клеток, реакции организма в целом не сводятся к реакциям отдельных клеток. Напомним универсальное правило: закономерности системы не могут быть сведены к закономерностям отдельных элементов.
Нервные клетки и некоторые ткани (мышечная, железистая) специально приспособлены к осуществлению быстрых реакций на раздражение. Такие клетки и ткани называются возбудимыми, а их реакция -возбудимостью. Клетки при возбуждинии переходят из состояния физиологического покоя в состояние активности. В частности, нервная клетка генерирует один, или несколько электрических импульсов. Это связано с тем, что при возбуждении проницаемость мембраны для ионов резко увеличивается. Возникают ионные токи, что естественно приводит к изменению разности потенциалов на поверхности мембраны. Это изменение мембранного потенциала называется потенциалом действия. Генерируемые нервными клетками импульсы также называются спайками. Группы, тесно следующих друг за другом спайков, называются пачками, или берстами. Амплитуды спайков относительно стабильны для для каждого типа нейронов, поэтому часто говорят, что нейрон реагирует на раздражение по закону “все, или ничего”.
Нервное возбуждение -распространяющийся процесс. Возникнув в одном, или нескольких нейронах, оно передается другим клеткам. Проведение возбуждения обусловлено тем, что потенциал действия, возникнув в одной клетке, становится раздражителем для связанных с ней клеток. То же самое относится к другим возбудимым тканям, например, к сердечной мышце. Согласно наиболее распространенной в настоящее время точки зрения считается, что “сообщения” в нервной системе передаются в виде импульсов “все, или ничего” в форме частотного кода.
Обсудим природу мембранного потенциала. Мембрана, отделяющая цитоплазму нейрона от межклеточной среды, состоит в основном из липидов -жироподобных веществ. В нее встроены белковые молекулы. Некоторые молекулы пронизывают липидный слой насквозь, а другие погружены лишь до сердцевины (своеобразные ворсинки). Некоторые белки выполняют роль каналов, осуществляющих транспорт ионов через мембрану. Другие -служат рецепторами, позволяющими нейрону реагировать на поступающие от других нейронов потенциалы действия.
Механизмы переноса ионов через мембрану делятся на два класса: пассивный и активный транспорт. Пассивный транспорт не требует затрат энергии. Он определяется двумя факторами. Диффузия способствует выравниванию концентрации растворов. Носители зарядов -ионы перемещаются под действием электрического поля. При активном транспорте за счет химической энергии, освобождающейся при окислении аминокислот, может осуществляться перенос ионов как в области с более высокой их концентрацией, так и против электрических сил.
Закономерности пассивного
транспорта опираются на некоторые положения электрохимии. Как уже говорилось,
мембраны биологического происхождения обладают избирательной проницаемостью.
Одни ионы достаточно легко диффундируют через них. Для других ионов мембраны
практически непроницаемы. Рассмотрим на примере положение об электрохимическом
равновесии. Пусть в сосуд ![]() с
раствором
с
раствором ![]() помещена полость
помещена полость ![]() , ограниченная мембраной,
где также находится раствор
, ограниченная мембраной,
где также находится раствор ![]() .
Обозначим через
.
Обозначим через ![]() и
и ![]() концентрации раствора в
сосуде и в полости. Предположим, что мембрана проницаема для ионов
концентрации раствора в
сосуде и в полости. Предположим, что мембрана проницаема для ионов ![]() и непроницаема для ионов
и непроницаема для ионов ![]() . Пусть концентрация расвора
в сосуде ниже, чем в полости, т.е.
. Пусть концентрация расвора
в сосуде ниже, чем в полости, т.е. ![]() . Тогда
ионы калия будут переходить из полости в сосуд, поскольку диффузия стремится
выровнять концентрации. В полости образуется относительный дефицит положительно
заряженных ионов и она заряжается отрицательно. Течнее, отрицательный заряд
сосредотачивается на внутренней поверхности мембраны. Наоборот, внешняя
поверхность мембраны заряжается положительно. Электрическое поле направлено
так, что диффузия положительных ионов
. Тогда
ионы калия будут переходить из полости в сосуд, поскольку диффузия стремится
выровнять концентрации. В полости образуется относительный дефицит положительно
заряженных ионов и она заряжается отрицательно. Течнее, отрицательный заряд
сосредотачивается на внутренней поверхности мембраны. Наоборот, внешняя
поверхность мембраны заряжается положительно. Электрическое поле направлено
так, что диффузия положительных ионов ![]() будет
затруднена. в результате при некоторой разности потенциалов
будет
затруднена. в результате при некоторой разности потенциалов ![]() между внутренней и внешней
поверхностью мембраны диффузия ионов вообще прекратится. Величина
между внутренней и внешней
поверхностью мембраны диффузия ионов вообще прекратится. Величина ![]() называется равновесным
электрохимическим потенциалом. Она вычисляется по формуле Нернста:
называется равновесным
электрохимическим потенциалом. Она вычисляется по формуле Нернста:
![]() ,
(1)
,
(1)
где ![]() -универсальная
газовая постоянная,
-универсальная
газовая постоянная, ![]() -абсолютная
температура,
-абсолютная
температура, ![]() -число Фарадея,
-число Фарадея, ![]() -заряд иона.
-заряд иона.
Пусть ![]() текущее значение
мембранного потенциала. привлечем некоторые положения теории электрических
цепей. Мембрана является диэлектриком (изолятором) и поэтому обладает
емкостью. Ток
текущее значение
мембранного потенциала. привлечем некоторые положения теории электрических
цепей. Мембрана является диэлектриком (изолятором) и поэтому обладает
емкостью. Ток ![]() , текущий через
емкость и напряжение
, текущий через
емкость и напряжение ![]() (оно же
мембранный потенциал) связаны соотношением:
(оно же
мембранный потенциал) связаны соотношением: ![]() ,
где коэффициент пропорциональности
,
где коэффициент пропорциональности ![]() называется
емкостью. Отметим, что в некотором смысле ток, текущий через мембрану, является
фиктивным. Он не сопровождается переносом зарядов. Согласно закону Нернста
мембрана является источником напряжения
называется
емкостью. Отметим, что в некотором смысле ток, текущий через мембрану, является
фиктивным. Он не сопровождается переносом зарядов. Согласно закону Нернста
мембрана является источником напряжения ![]() .
Ток
.
Ток ![]() , текущий через источник
напряженим
, текущий через источник
напряженим ![]() , связан с напряжением
, связан с напряжением ![]() на его полюсах формулой:
на его полюсах формулой: ![]() . По закону Кирхгофа сумма
токов равна нулю:
. По закону Кирхгофа сумма
токов равна нулю: ![]() . Таким образом,
получаем дифференциальное уравнение:
. Таким образом,
получаем дифференциальное уравнение:
![]() .
(2)
.
(2)
Проведем тривиальный анализ уравнения (2). Перепишем его в виде:
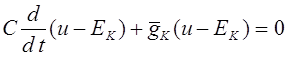 .
.
Отсюда получаем:
![]() .
.
Таким образом, по экспоненте
мембранный потенциал ![]() при
при ![]() .
.
Сделаем ряд замечаний. При
анализе уравнения (2) ы предполагали, что коэффициенты ![]() и
и ![]() не зависят от
не зависят от ![]() . Действительно для мембраны
емкость практически постоянна. Однако, проводимость
. Действительно для мембраны
емкость практически постоянна. Однако, проводимость ![]() есть
функция от
есть
функция от ![]() . Проведенный анализ
справедлив лишь при малых отклонениях
. Проведенный анализ
справедлив лишь при малых отклонениях ![]() от
равновесного значения
от
равновесного значения ![]() .
.
Пусть теперь дополнительно к
![]() в полости и в сосуде
присутствует
в полости и в сосуде
присутствует ![]() , концентрации которого в
полости и в сосуде различны. Ионам
, концентрации которого в
полости и в сосуде различны. Ионам ![]() отвечает
свое равновесное значение
отвечает
свое равновесное значение ![]() .
Натриевый ток
.
Натриевый ток ![]() связан с
мембранным потенциалом
связан с
мембранным потенциалом ![]() соотношением:
соотношением: ![]() . Привлекая снова закон
Киргофа, получаем:
. Привлекая снова закон
Киргофа, получаем:
![]() . (3)
. (3)
Теперь в силу (3) равновесное значение мембранного потенциала суть:
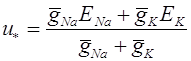 .
.
Одна из первых гипотез о
природе мембранного потенциала была высказана в 1902 г. Бернштейном, который
использовал положения электрохимии. Он предположил, что предположил, что
концентрация ионов ![]() в клетке выше,
чем во внеклеточной среде. Вследствие этого ионы
в клетке выше,
чем во внеклеточной среде. Вследствие этого ионы ![]() диффундируют
из клетки. Образуется их относительный дефицит положительных ионов внутри
клетки и внутренняя поверхность мембраны заряжается отрицательно. Тем самым,
потенциал покоя определяется равновесным электрохимическим потенциалом для
ионов
диффундируют
из клетки. Образуется их относительный дефицит положительных ионов внутри
клетки и внутренняя поверхность мембраны заряжается отрицательно. Тем самым,
потенциал покоя определяется равновесным электрохимическим потенциалом для
ионов ![]() . Далее, Бернштейн
предположил, что в жизни нейрона иногда наступает особый момент -состояние
возбуждения, когда на короткое время мембрана становится проницаемой и для
других ионов, в частности, для натрия и хлора. В результате притока внутрь
клетки положительных ионов величина мембранного потенциала падает, а затем,
после восстановления избирательных свойств мембраны, снова входит в норму. Так
впервые была объснена генерация спайка.
. Далее, Бернштейн
предположил, что в жизни нейрона иногда наступает особый момент -состояние
возбуждения, когда на короткое время мембрана становится проницаемой и для
других ионов, в частности, для натрия и хлора. В результате притока внутрь
клетки положительных ионов величина мембранного потенциала падает, а затем,
после восстановления избирательных свойств мембраны, снова входит в норму. Так
впервые была объснена генерация спайка.
Натриево - калиевый цикл
Гипотеза Бернштейна хорошо объясняла многие известные физиологам того времени факты. В частности, зависимость потенциала покоя от концентрации калия в межклеточной среде, а также от температуры. Однако в то время гипотезу нельзя было подвергнуть экспериментальной проверке. В распоряжении исследователей не было методики непосредственного изменения мембранного потенциала и концентраций ионов. Гипотеза Бернштейна вызывала массу споров.
Ситуация изменилась после сообщения английского зоолога Дж. Юнга, сделанного в 1936 г. Он обнаружил, что длинные тяжи у кальмаров и каракатиц являются не кровеносными сосудами, как это считалось ранее, а необычайно толстыми аксонами (отростками нервных клеток). Они получили название гигантских аксонов и стали естественным объектом для изучения мембран. Диаметр аксонов достигает 1 мм и дает возможность вводить в них электроды и капилляры. В результате можно измерить как мембранный потенциал, так и концентрацию внутриклеточного раствора.
Выяснилось, что мембранная
теория Бернштейна в целом верна, хотя и нуждается во внесении ряда существенных
дополнений и изменений. В частности верным оказалось утверждение, что потенциал
покоя обусловлен в основном электрохимическим потенциалом ионов ![]() . Наоборот, согласно теории
Бернштейна в точке максимума потенциала действия (спайка) мембранный потенциал
должен быть равен нулю (ток ионов прекращается, когда напряжение равно нулю).
Однако, английские физиологи А. Ходжкин и А. Хаксли в 1939 г. показали, что на
максимуме потенциала действия мембранный потенциал не уничтожается, а меняет
знак. Внешняя поверхность мембраны заряжается положительно по отношению к
внутренней. Явление получило название “овершут” и не имело объяснений в
рамках теории Бернштейна. Оно связано с неравномерным распределением ионов
натрия. Оказалось, что концентрация ионов
. Наоборот, согласно теории
Бернштейна в точке максимума потенциала действия (спайка) мембранный потенциал
должен быть равен нулю (ток ионов прекращается, когда напряжение равно нулю).
Однако, английские физиологи А. Ходжкин и А. Хаксли в 1939 г. показали, что на
максимуме потенциала действия мембранный потенциал не уничтожается, а меняет
знак. Внешняя поверхность мембраны заряжается положительно по отношению к
внутренней. Явление получило название “овершут” и не имело объяснений в
рамках теории Бернштейна. Оно связано с неравномерным распределением ионов
натрия. Оказалось, что концентрация ионов ![]() внутри
клетки примерно в десять раз ниже чем в межклеточной жидкости. В начале спайка
ионы натрия под действием электрического поля и концентрационного градиента
устремляются из межклеточной среды в клетку (в клетке их концентрация ниже, а
внутренняя поверхность мембраны заряжена отрицательно по отношению к внешней).
В этом гипотеза Бернштейна оказалась верной. После смены знака мембранного
потенциала ионы натрия продолжают перемещаться в клетку только под действием
концентрационного градиента. Мебранный потенциал на максимуме овершута
приближается к равновесному электрохимическому потенциалу для ионов
внутри
клетки примерно в десять раз ниже чем в межклеточной жидкости. В начале спайка
ионы натрия под действием электрического поля и концентрационного градиента
устремляются из межклеточной среды в клетку (в клетке их концентрация ниже, а
внутренняя поверхность мембраны заряжена отрицательно по отношению к внешней).
В этом гипотеза Бернштейна оказалась верной. После смены знака мембранного
потенциала ионы натрия продолжают перемещаться в клетку только под действием
концентрационного градиента. Мебранный потенциал на максимуме овершута
приближается к равновесному электрохимическому потенциалу для ионов ![]() . В дальнейшем пронуцаемость
мембраны для ионов натрия падает и активируется проводимость для ионов колия,
которые движутся из клетки, где их концентрация выше. Ионы калия уносят из
клетки положительный заряд. Внутренняя поверхность мембраны заряжается
отрицательно. Этот натриево -калиевый цикл ниже будет рассмотрен
подробнее.
. В дальнейшем пронуцаемость
мембраны для ионов натрия падает и активируется проводимость для ионов колия,
которые движутся из клетки, где их концентрация выше. Ионы калия уносят из
клетки положительный заряд. Внутренняя поверхность мембраны заряжается
отрицательно. Этот натриево -калиевый цикл ниже будет рассмотрен
подробнее.
В течение цикла ионы натрия заходят в клетку, а ионы калия ее покидают. Такое замещение должно выравнивать концентрации ионов. Казалось бы, что после ряда циклов нервная клеткане должна генерировать спайков (концентрации ионов внутри и вне клетки уравняются). В действительности это не так. Неравномерное распределение ионов внутри и вне клетки поддерживается активным транспортом ионов. Механизмы, осуществляющие транспорт ионов через мембрану в сторону повышенной концентрации, называются мембранными насосами (помпами). Они потребляют энергию, которая освобождается в результате окисления аминокислот.
Наиболее изучен натриевый
насос. Он выводит ионы ![]() из клетки и
одновременно транспортирует ионы
из клетки и
одновременно транспортирует ионы ![]() внутрь
клетки. Этот процесс включает в себя обязательный обмен двух ионов
внутрь
клетки. Этот процесс включает в себя обязательный обмен двух ионов ![]() во внешней среде на три
иона
во внешней среде на три
иона ![]() в клетке (если удалить из
среды ионы
в клетке (если удалить из
среды ионы ![]() , то ионы
, то ионы ![]() из клетки выводиться уже не
будут). Если мембранный потенциал отрицателен (внутренняя поверхность мембраны
заряжена отрицательно), то натриевый насос выполняет электрическую работу,
выводя из клетки суммарно один положительный заряд. Натриевый насос действует
избирательно. Например, он не способен переносить ионы лития. Молекулярный
механизм активного транспорта в настоящее время до конца не ясен.
из клетки выводиться уже не
будут). Если мембранный потенциал отрицателен (внутренняя поверхность мембраны
заряжена отрицательно), то натриевый насос выполняет электрическую работу,
выводя из клетки суммарно один положительный заряд. Натриевый насос действует
избирательно. Например, он не способен переносить ионы лития. Молекулярный
механизм активного транспорта в настоящее время до конца не ясен.
Натриевый насос - один из
главных механизмов, благодаря которому внутри клетки поддерживается избыточная
по сравнению с внешней средой концентрация ионов ![]() и
недостаточная, примерно в десять раз меньшая, чем во внеклеточной жидкости,
концентрация ионов
и
недостаточная, примерно в десять раз меньшая, чем во внеклеточной жидкости,
концентрация ионов ![]() .
.
Для исследования процесса генерации спайка А.Ходжкиным и А.Хаксли был разработан оригинальный прием, который называется методом фиксации потенциала. Внутриклеточно водятся электроды и используется система с обраной связью, позволяющая позволяющая поддерживать мембранный потенциал на любом заданном уровне. Тем самым, можно имитировать различные фазы потенцила действия, как-бы “замораживая” его. Система позволяет измерять ионные токи. Изменяя ионный состав среды (так же через микрокапилляры меняют состав внутриклеточной жидкости) можно можно итентифицировать ионы, которые обуславливают ток. Исследования обнаружили, что даже пассивный транспорт ионов (в соответствии с градиентом концентраций и направлением электрического поля) подчиняется специфическим закономерностям. Для их объяснения А.Ходжкиным и А.Хаксли была высказана гипотеза о наличии в мембране специальных ионных каналов, служащих для их транспортировки.
При положительном отклонении
мембранного потенциала от потенциала в состоянии покоя (значение потенциала
уменьшается по абсолютной величине) активируются, т.е. открываются каналы для ![]() , пропускающие эти ионы
внутрь клетки. Ионы
, пропускающие эти ионы
внутрь клетки. Ионы ![]() движутся в
соответствии с направлением электрического поля, причем в область с меньшей
концентрацией. Каналы играют роль селективных (избирательных) фильтров,
пропускающих ионы
движутся в
соответствии с направлением электрического поля, причем в область с меньшей
концентрацией. Каналы играют роль селективных (избирательных) фильтров,
пропускающих ионы ![]() и непроницаемых
для других ионов. Механизмы, приводящие к открытию и закрытию каналов,
называются воротами. При деполяризации (уменьшении абсолютной величины
мембранного потенциала) открываются активационные так называемые
и непроницаемых
для других ионов. Механизмы, приводящие к открытию и закрытию каналов,
называются воротами. При деполяризации (уменьшении абсолютной величины
мембранного потенциала) открываются активационные так называемые ![]() -ворота для натриевых
каналов. Чем силнее деполяризована мембрана, тем больше
-ворота для натриевых
каналов. Чем силнее деполяризована мембрана, тем больше ![]() -ворот открыто, что в свою
очередь уделичивает деполяризацию. Процесс открытия ворот протекает
лавинообразно.
-ворот открыто, что в свою
очередь уделичивает деполяризацию. Процесс открытия ворот протекает
лавинообразно.
При относительно длительной
деполяризации натриевые каналы инативируются. Срабатывают так называемые ![]() -ворота, которые блокируют
каналы через время порядка 1 мсек после открытия
-ворота, которые блокируют
каналы через время порядка 1 мсек после открытия ![]() -ворот.
В 1980 г. Ф. Сигворс и Э. Неер зарегистрировали токи через единичные натриевые
каналы. Оказалось, что они подчиняются закону “все или ничего”, Открываются
практически мгновенно, а через время около 1 мсек. так же практически мгновенно
закрываются. Ионные каналы представляют собой молекулы бека, вкрапленные в
липидный слой мембраны.
-ворот.
В 1980 г. Ф. Сигворс и Э. Неер зарегистрировали токи через единичные натриевые
каналы. Оказалось, что они подчиняются закону “все или ничего”, Открываются
практически мгновенно, а через время около 1 мсек. так же практически мгновенно
закрываются. Ионные каналы представляют собой молекулы бека, вкрапленные в
липидный слой мембраны.
В районы максимума пика
потенциала действия большинство натриевых каналов инактивируется, т.е.
закрываются ![]() -ворота. Встает вопрос:
каким образом мембранный потенциал возвращается к исходному уровню -состоянию
покоя? Экспериментально А. Ходжкин и А. Хаксли обнаружили, что с некоторым
запаздыванием по отношению к началу натриевого тока возникает калиевый ток.
Ионы калия начинают покидать клетку, поскольку активируются калиевые каналы.
Гипотеза связывает это с открытием так называемых
-ворота. Встает вопрос:
каким образом мембранный потенциал возвращается к исходному уровню -состоянию
покоя? Экспериментально А. Ходжкин и А. Хаксли обнаружили, что с некоторым
запаздыванием по отношению к началу натриевого тока возникает калиевый ток.
Ионы калия начинают покидать клетку, поскольку активируются калиевые каналы.
Гипотеза связывает это с открытием так называемых ![]() -ворот.
Ионы калия движутся в область с меньшей концентрацией (пассивный транспорт).
При этом в районе овершута (мембранный потенциал положителен) движение
осуществляется в соответствии с направлением электрического поля. Калиевый ток уносит
из клетки (точнее с внутренней поверхности мембраны) отрицательный заряд.
Мембрана снова поляризуется.
-ворот.
Ионы калия движутся в область с меньшей концентрацией (пассивный транспорт).
При этом в районе овершута (мембранный потенциал положителен) движение
осуществляется в соответствии с направлением электрического поля. Калиевый ток уносит
из клетки (точнее с внутренней поверхности мембраны) отрицательный заряд.
Мембрана снова поляризуется.
Считается, что в отличие от
натриевых каналов, для калиевых каналов нет инактивационных ворот.
Активационные ![]() -ворота сами
закрываются, когда мембрана возвращается к уровню потенциала покоя
(реполяризуется).
-ворота сами
закрываются, когда мембрана возвращается к уровню потенциала покоя
(реполяризуется).
Важна отметить, что
количество ионов, которое проходит через мембрану при одиночном потенциале
действия, практически не вызывает изменения внутриклеточных концентраций ионов.
Исключение могут составлять лишь мельчайшие нервные клетки. По некоторым
оценкам при одном потенциале действия содержание ![]() внутри
гигантского аксона кальмара изменяется всего лишь на
внутри
гигантского аксона кальмара изменяется всего лишь на ![]() от исходного. Если
блокировать активные натриевые насосы каким-нибудь ядом, то аксон все равно
сможет сгенерировать несколько тысяч импульсов. Непосредственно активный
транспорт не участвует в генерации спайков. Однако, он поддерживает на должном
уровне концентрационные градиенты, наличие которых приводит к возникновению
потенциалов действия.
от исходного. Если
блокировать активные натриевые насосы каким-нибудь ядом, то аксон все равно
сможет сгенерировать несколько тысяч импульсов. Непосредственно активный
транспорт не участвует в генерации спайков. Однако, он поддерживает на должном
уровне концентрационные градиенты, наличие которых приводит к возникновению
потенциалов действия.
После описания механизма генерации спайка, обратимся к системе уравнений, описывающей это процесс. Она предложена А. Ходжкиным и А. Хаксли.
Аксон Ходжкина - Хаксли
Модель базируется на
электрохимическом уравнении (3). Мембранный потенциал будем отсчитывать от его
уровня ![]() в состоянии покоя, т.е.
положим
в состоянии покоя, т.е.
положим ![]() , или же
, или же ![]() . Аналогично введем
обозначения для отсчитываемых от
. Аналогично введем
обозначения для отсчитываемых от ![]() равновесных
электрохимических потенциалов
равновесных
электрохимических потенциалов ![]() и
и ![]() . Ясно, что сохраняются
разности:
. Ясно, что сохраняются
разности: ![]() и
и ![]() . В создании мембранного
потенциала кроме ионов
. В создании мембранного
потенциала кроме ионов ![]() и
и ![]() принимают участие и другие
ионы, в частности, ионы
принимают участие и другие
ионы, в частности, ионы ![]() .
Обозначим их суммарный электрохимический потенциал через
.
Обозначим их суммарный электрохимический потенциал через ![]() , соответственно
, соответственно ![]() . В уравнение (3) для
баланса мембранных токов следует добавить слагаемое
. В уравнение (3) для
баланса мембранных токов следует добавить слагаемое ![]() .
Данный ток называется током утечки. Для гигантского аксона кальмара А.
Ходжкиным и А. Хаксли были экспериментально найдены значения:
.
Данный ток называется током утечки. Для гигантского аксона кальмара А.
Ходжкиным и А. Хаксли были экспериментально найдены значения: ![]() мв,
мв, ![]() мвт,
мвт, ![]() мвт.
мвт.
Электрохимическое уравнение
(3) суть обыкновенное дифференциальное уравнение первого порядка. Как показано
выше, его коэффициенты следует считать функциями от мембранного потенциала ![]() . По биологическому смыслу
решения уравнения ограничены на положительной полуоси
. По биологическому смыслу
решения уравнения ограничены на положительной полуоси ![]() . Можно доказать, что все
решения такого уравнения монотонно стремятся к состояниям равновесия. Объяснить
в рамках одного электрохимического уравнения генерацию потенциала действия
невозможно.
. Можно доказать, что все
решения такого уравнения монотонно стремятся к состояниям равновесия. Объяснить
в рамках одного электрохимического уравнения генерацию потенциала действия
невозможно.
Из приведенных выше
построений следует, проводимости ![]() и
и ![]() следует считать функциями
не только мембранного потенциала
следует считать функциями
не только мембранного потенциала ![]() , но и
времени. Нижеследующие построения А. Ходжкина и А. Хаксли во многом носят
феноменологический характер, т.е. не имееют под собой прочной теоретической
основы и опираются на ряд допущений и догадок. Рассмотрим натриевую
проводимость. Для описания ее зависимости от времени и мембранного потенциала
А. Ходжкин и А. Хаксли ввели две новые переменные
, но и
времени. Нижеследующие построения А. Ходжкина и А. Хаксли во многом носят
феноменологический характер, т.е. не имееют под собой прочной теоретической
основы и опираются на ряд допущений и догадок. Рассмотрим натриевую
проводимость. Для описания ее зависимости от времени и мембранного потенциала
А. Ходжкин и А. Хаксли ввели две новые переменные ![]() и
и
![]() , которые характеризуют
процессы активации и инактивации натриевых каналов. В интерпретации авторов
, которые характеризуют
процессы активации и инактивации натриевых каналов. В интерпретации авторов ![]() -вероятность открытия
-вероятность открытия ![]() -ворот,
-ворот, ![]() -вероятность закрытия
-вероятность закрытия ![]() -ворот, или же -отношение
числа открытых и закрытых ворот соответствующего типа к числу каналов на
поверхности мембраны единичной площади. Авторы модели положили:
-ворот, или же -отношение
числа открытых и закрытых ворот соответствующего типа к числу каналов на
поверхности мембраны единичной площади. Авторы модели положили: ![]() , где коэффициент
, где коэффициент ![]() был назван максимальной
натриевой проводимостью. Предложенное А. Ходжкиным и А. Хаксли обоснование вида
зависимости в настоящее время выглядит искуственным. Методом подбора были
выписаны линейные обыкновенные уравнения первого порядка для переменных
был назван максимальной
натриевой проводимостью. Предложенное А. Ходжкиным и А. Хаксли обоснование вида
зависимости в настоящее время выглядит искуственным. Методом подбора были
выписаны линейные обыкновенные уравнения первого порядка для переменных ![]() и
и ![]() . При этом в уравнение для
. При этом в уравнение для ![]() не входит переменная
не входит переменная ![]() , а в уравнение для
, а в уравнение для ![]() не входит
не входит ![]() . Коэффициенты уравнений
зависят только от мембранного потенциала
. Коэффициенты уравнений
зависят только от мембранного потенциала ![]() .
Более менее убедительное обоснование необходимости именно такой зависимости
отсутствует.
.
Более менее убедительное обоснование необходимости именно такой зависимости
отсутствует.
Для описания изменения
калиевой проводимости ![]() А. Ходжкиным и А.
Хаксли была введена функция
А. Ходжкиным и А.
Хаксли была введена функция ![]() . Она
интерпретировалась как вероятность открытия
. Она
интерпретировалась как вероятность открытия ![]() -ворот
для каливых каналов, т.е. как вероятность активации последних. Напомним, что по
гипотезе А. Ходжкина и А. Хаксли инактивационные ворота для каливых каналов
отсутствуют. Авторы опытным путем подобрали линейное обыкновенное
дифференциальное уравнение для
-ворот
для каливых каналов, т.е. как вероятность активации последних. Напомним, что по
гипотезе А. Ходжкина и А. Хаксли инактивационные ворота для каливых каналов
отсутствуют. Авторы опытным путем подобрали линейное обыкновенное
дифференциальное уравнение для ![]() и
положили
и
положили ![]() . Коэффициенты уравнения
зависят только от мембранного потенциала
. Коэффициенты уравнения
зависят только от мембранного потенциала ![]() .
Коэффициент
.
Коэффициент ![]() называется максимальной
калиевой проводимостью.
называется максимальной
калиевой проводимостью.
Относительно проводимости ![]() для тока утечки А. Ходжкин
и А. Хаксли предложили считать его постоянным:
для тока утечки А. Ходжкин
и А. Хаксли предложили считать его постоянным: ![]() .
В результате для описания процесса генерации потенциала действия была
предложена система четырех уравнений, Первое из них -электрохимическое
уравнение для баласа мембранных токов токов:
.
В результате для описания процесса генерации потенциала действия была
предложена система четырех уравнений, Первое из них -электрохимическое
уравнение для баласа мембранных токов токов: ![]() .
Напомним, что
.
Напомним, что
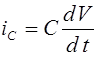 ,
, ![]() , (4)
, (4)
![]() ,
, ![]() .
(5)
.
(5)
Второе и третье уравнения
описывают соответственно процессы открытия ![]() и
закрытия
и
закрытия ![]() -ворот для натриевых
каналов. Наконец, четвертое уравнение отражает процесс открытия
-ворот для натриевых
каналов. Наконец, четвертое уравнение отражает процесс открытия ![]() -ворот для калиевых
каналов. Система уравнений Ходжкина -Хаксли имеет следующий вид:
-ворот для калиевых
каналов. Система уравнений Ходжкина -Хаксли имеет следующий вид:
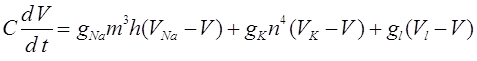 , (6)
, (6)
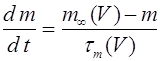 , (7)
, (7)
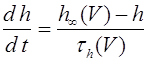 ,
(8)
,
(8)
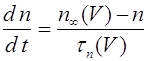 ,
(9)
,
(9)
где, напомним, ![]() ,
, ![]() ,
, ![]() . В (7) -(9) функции
. В (7) -(9) функции ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() положительны и непрерывны.
Функции
положительны и непрерывны.
Функции ![]() ,
, ![]() ,
, ![]() относятся к классу так
называемых сигмоидных функций, т.е. они монотонны обладают следующими
свойствами:
относятся к классу так
называемых сигмоидных функций, т.е. они монотонны обладают следующими
свойствами: ![]() ,
, ![]() ,
, ![]() при
при ![]() и
и ![]() ,
, ![]() ,
, ![]() при
при ![]() . В работах А. Ходжкина и А.
Хаксли указан их конкретный вид. Функции весьма сложно устроены. Реально
система уравнений допускает только численное исследование. Ограничимся рядом
замечаний на качественном уровне, иллюстрирующих впечатления от численного
исследования. Входящие в систему (6) -(9) функции подобраны так, что выполнен
ряд свойств. Она имеет устойчивое состояние равновесия
. В работах А. Ходжкина и А.
Хаксли указан их конкретный вид. Функции весьма сложно устроены. Реально
система уравнений допускает только численное исследование. Ограничимся рядом
замечаний на качественном уровне, иллюстрирующих впечатления от численного
исследования. Входящие в систему (6) -(9) функции подобраны так, что выполнен
ряд свойств. Она имеет устойчивое состояние равновесия ![]() , где
, где ![]() ,
, ![]() -положительны. Пусть
-положительны. Пусть ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Если значение
. Если значение ![]() не слишком велико, то в
силу устойчивости состояния равновесия с течением времени
не слишком велико, то в
силу устойчивости состояния равновесия с течением времени ![]() . Существует такое пороговое
значение
. Существует такое пороговое
значение ![]() , что при
, что при ![]() решения системы ведут себя
по другому. Первоначально
решения системы ведут себя
по другому. Первоначально ![]() убывает.
Однако начинает расти величина
убывает.
Однако начинает расти величина ![]() . Слагаемое
. Слагаемое
![]() уравнении (6) положительно,
т.к.
уравнении (6) положительно,
т.к. ![]() , а
, а ![]() близко к нулю. В результате
производная
близко к нулю. В результате
производная ![]() становится положительной.
Мембранный потенциал начинает расти (момент начала генерации спайка). Вместе с
ним растет и величина
становится положительной.
Мембранный потенциал начинает расти (момент начала генерации спайка). Вместе с
ним растет и величина ![]() , что приводит к
дальнейшему увеличению
, что приводит к
дальнейшему увеличению ![]() и ускорению роста
и ускорению роста
![]() . Однако, чуть позже
начинает уменьшаться величина
. Однако, чуть позже
начинает уменьшаться величина ![]() . Это
замедляет рост
. Это
замедляет рост ![]() , тем более, что
уменьшается разность
, тем более, что
уменьшается разность ![]() . Одновременно
растет величина
. Одновременно
растет величина ![]() . Соответствующее
слагаемое
. Соответствующее
слагаемое ![]() в уравнении (6)
отрицательно, т.к.
в уравнении (6)
отрицательно, т.к. ![]() и
и ![]() . Существует момент времени
. Существует момент времени ![]() , где
, где ![]() . Это точка максимума
потенциала действия. Значение мембранного потенциала
. Это точка максимума
потенциала действия. Значение мембранного потенциала ![]() относительно близко к
относительно близко к ![]() . После прохождения точки
максимума значение производной
. После прохождения точки
максимума значение производной ![]() определяется
значением слагаемого
определяется
значением слагаемого ![]() и становится
отрицательным. Скорость убывания мембранного потенциала на нисходящем участке
спайка меньше по абсолютной величине, чем скорость роста на восходящем участке.
Нисходящий участок продолжительнее восходящего. В дальнейшем значение
и становится
отрицательным. Скорость убывания мембранного потенциала на нисходящем участке
спайка меньше по абсолютной величине, чем скорость роста на восходящем участке.
Нисходящий участок продолжительнее восходящего. В дальнейшем значение ![]() становится отрицательным, а
после этого
становится отрицательным, а
после этого ![]() . Величины
. Величины ![]() ,
, ![]() ,
, ![]() также стремятся к своим
равновесным значениям. Процесс генерации спайка закончен.
также стремятся к своим
равновесным значениям. Процесс генерации спайка закончен.
Особо подчеркнем значимость
факта, что система (6) -(7) обладает пороговыми свойствами. Существует такое
критическое значение ![]() мембранного
потенциала, что при начальном отклонении мембранного потенциала
мембранного
потенциала, что при начальном отклонении мембранного потенциала ![]() с течением времени значение
с течением времени значение
![]() . Если же
. Если же ![]() , то через некоторое время
(его называют скрытым, или латентным периодом) генерируется спайк. Мадель
адекватно отражает пороговые свойства реального аксона. Если воздействовать на
мембрану кратковременным толчком деполяризующего тока (отклоняющего мембранный
потенциал в положительном направлении), то после слабого воздействия мембранный
потенциал возвращается в равновесное состояние. Вследствие достаточно сильного
воздействия спустя латентный период генерируется спайк.
, то через некоторое время
(его называют скрытым, или латентным периодом) генерируется спайк. Мадель
адекватно отражает пороговые свойства реального аксона. Если воздействовать на
мембрану кратковременным толчком деполяризующего тока (отклоняющего мембранный
потенциал в положительном направлении), то после слабого воздействия мембранный
потенциал возвращается в равновесное состояние. Вследствие достаточно сильного
воздействия спустя латентный период генерируется спайк.
Обсудим еще одно свойство аксона. Гигантские аксоны достигают длины нескольких десятков сантиметров. Мебранный потенциал на разных участках аксона может различаться. Аксон представляет собой так называемую распределенную систему. Если подействовать на некоторый участок аксона допороговым деполяризующим толчком тока, то мембранный потенциал на этом и некотором примыкаюшем к нему участке отклонится от равновесного состояния в положительном направлении. Такое отклонение называется локальным ответом. Возмущение с течением времени затухает, одновременно, как капля, растекаясь по аксону. В результате локальные ответы, возникшие при стимулировании различных участков, могут накладываться друг на друга, т.е., как говорят, суммироваться по пространству. Если же на участок аксона повторно подается деполяризирующий ток, то новый локальный ответ накладывается на предыдущий. Говорят, что происходит временное суммирование. Локальные ответы градуальны. Их амплитуда зависит от силы стимула (точнее, силы -длительности). В случае, когда локальный ответ в результате суммации, или же после достаточно сильного одноразового локального воздействия достигает порогового уровня, запускаются механизмы генерации потенциала действия. Зародившись локально, потенциал действия распространяется по аксону.
Явление распространения объясняется следующим образом. Цитоплазма - электролит, а, следовательно, хороший проводник. Если между точками существуют ненулевые разности потенциалов, то вдоль мембраны возникают токи (вблизи поверхности). Они направлены от точек с более высоким потенциалом к точкам, где он меньше, и подчиняются закону Ома. Вследствие этого потенциал на участках, прилегающих, к области генерации спайка, растет и достигает порогового значения. В результате эти участки сами генерируют потенциалы действия. Процесс распространяется вдель аксона.
Проведение нервных импульсов обладает важной особенностью. При “столкновении” они аннигилируют, т.е. уничтожаются. С помощью локального воздействия возбудим аксон в двух точках. По нему будут распространяться четыре импульса, два из которых движутся во встречных направлениях. Данные импульсы встретятся и не пропустят друг друга. Это связано с тем, что мембрана обладает следующим свойством. Во время потенциала действия и некоторое время после его завершения она не реагирует на воздействие. В частности, после завершения спайка некоторое время не способна сгенерировать нового потенциала действия. Данное состояние называется абсолютной рефрактерностью. Отметим, что постепенно абсолютная рефрактерность сменяется относительной. Для того, чтобы инициировать потенциал действия в состоянии относительной рефрактерности, нужно применить более мощный стимул, нежели в состоянии покоя.
Для описания процесса
распространения потенциала действия вдоль аксона А. Ходжкин и А. Хксли
модернизировали уравнение (6). Пусть ![]() -координата
точки вдоль аксона, а
-координата
точки вдоль аксона, а ![]() -значение
мембранного потенциала в этой точке. Используется закон Ома, согласно которому
ток через сечение пропорционален градиенту напряжения (в одномерном случае
-производной). Ток через сечение
-значение
мембранного потенциала в этой точке. Используется закон Ома, согласно которому
ток через сечение пропорционален градиенту напряжения (в одномерном случае
-производной). Ток через сечение ![]() равен
равен 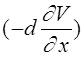 , где направление выбрано в
сторону возрастания
, где направление выбрано в
сторону возрастания ![]() , коэффициент
, коэффициент ![]() -проводимость. Выделим
участок аксона, координаты точек которого заключены в интервале
-проводимость. Выделим
участок аксона, координаты точек которого заключены в интервале ![]() . Суммарный ток через
сечения
. Суммарный ток через
сечения ![]() и
и ![]() равен
равен 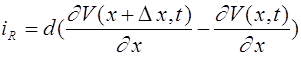 . Используя формулу Лагранжа
получим:
. Используя формулу Лагранжа
получим: 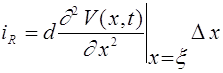 , где
, где ![]() . Через поверхность мембраны
выбранного участка аксона проходят емкостной
. Через поверхность мембраны
выбранного участка аксона проходят емкостной ![]() ,
натриевый
,
натриевый ![]() , калиевый
, калиевый ![]() токи, а также ток утечки
токи, а также ток утечки ![]() . Пусть
. Пусть ![]() . Суммарный мембранный ток
приближенно равен
. Суммарный мембранный ток
приближенно равен ![]() . Привлекая закон
Кирхгофа, получим:
. Привлекая закон
Кирхгофа, получим: ![]() . Используя
приведенные ранее формулы (4), (5) для мембранных токов и устремляя
. Используя
приведенные ранее формулы (4), (5) для мембранных токов и устремляя ![]() к нулю, приходим к
уравнению:
к нулю, приходим к
уравнению:
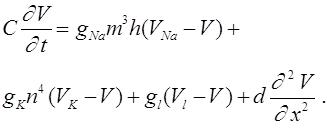 (10)
(10)
Его часто называют уравнением
аксона Ходжкина -Хаксли. В (10) функции ![]() ,
,
![]() ,
, ![]() как и выше подчиняются уравнениям
(7) -(9).
как и выше подчиняются уравнениям
(7) -(9).
А. Ходжкин и А. Хаксли
исследовали так называемые автоволновые решения системы уравнений, т. е.
решения типа бегущих волн: ![]() (аналогично
для
(аналогично
для ![]() ,
, ![]() ,
, ![]() ). Здесь параметр
). Здесь параметр ![]() -скорость распространения
волны. После подстановки в (11) для
-скорость распространения
волны. После подстановки в (11) для ![]() получается
обыкновенное дифференциальное уравнение:
получается
обыкновенное дифференциальное уравнение:
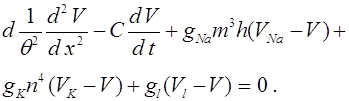 (11)
(11)
Система (7) -(9), (11)
исследовалась численно. Методом подбора было найдено значение скорости ![]() , при которой система
уравнений имела приемлемое по мнению авторов решение. Параметры полученного при
исследовании системы уравнений распространяющегося потенциала действия
оказались близкими к реально надлюдаемым в эксперименте.
, при которой система
уравнений имела приемлемое по мнению авторов решение. Параметры полученного при
исследовании системы уравнений распространяющегося потенциала действия
оказались близкими к реально надлюдаемым в эксперименте.
Скорость распространения импульса по гигантскому аксону относительно не велика (по сравнению с аналогичными по назначению проводниками нервных импульсов у человека). Она растет с увеличением диаметра аксона. Увеличение диаметров аксонов избрала природа для высокоскоростного проведения импульсов у беспозвоночных. Однако, когда организму нужна не только быстрота реакции, но и огромное количество связей, гигантские аксона становятся не приемлимыми. Например, в зрительном нерве, где больше миллиона связей, для больших аксонов не хватило бы места. Длинные аксоны у человека и позвоночных животных покрыты достаточно толстым липидным слоем -миелиновой оболочкой (точнее, они обвиты клетками содержащими и вырабатывающими миелин). В миелиновой оболочке присутствуют регулярно расположенные разрывы, где мембрана аскона оголена. Разрывы называются перехватами Ранвье. Миелинизированные участки иеют длину порядка 1 -2 мм. Протяженность перехватов Ранвье около 1 мкм. Перехваты Равье способны генерировать спайки. Миелинизиро-ванные участки обладают емкостью и омическим сопротивлением, но они не генерируют спайков. Импульсы по миелинизированным участкам рапространяются пассивно, т.е. с затратами энергии на омическое сопротивление и на перезаряд участка, предствляющего собой конденсатор (обратимые потери). Суммарно затраты энергии не велики.
Рассмотрим миелинизированный участок, ограниченный двумя перехватами. Пусть левый перехват генерирует спайк. Возмущение (положительное) по миелинизированному участку передается правому перехвату. Когда отклонение мембранного потенциала правого участка достигает порогового значения, он генерирует спайк. Этот импульс не может вызвать генерацию нового спайка левым перехватом Ранвье, поскольку тот находится в рефрактерном состоянии (в состояниии невосприимчивости). Однако, данный перехват по той же схеме возбуждает перехват, следуюший за ним справа. По миелинизированному аксону, перескакивая от перехвата к перехвату, будет распространяться импульс. Процесс называется сальтаторным проведением возбуждения (saltare - прыгать). Оно обеспечивает скорость распространения импульсов в 20- 25 раз более высокую, чем в гигантских аксонах того же диаметра.
Описанный процесс
сальтаторного проведения импульсов легко формализуется. В простейшем случае это
выглядит следующим образом. Пусть ![]() и
и ![]() - мембранные потенцилы
левого и правого перехвотов Ранвье, а
- мембранные потенцилы
левого и правого перехвотов Ранвье, а ![]() -потенциал
миелинизированного участка (считаем его во всех точках участка одинаковым).
Тогда между участком и соответствующими перехватами проходят токи:
-потенциал
миелинизированного участка (считаем его во всех точках участка одинаковым).
Тогда между участком и соответствующими перехватами проходят токи: 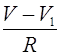 и
и 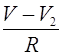 , где
, где ![]() -сопротивление перехода от
перехвата к миелинизированному участку. Через миелиновую оболочку проходят
емостной ток
-сопротивление перехода от
перехвата к миелинизированному участку. Через миелиновую оболочку проходят
емостной ток ![]() и ток утечки
и ток утечки ![]() , где
, где ![]() - суммарная емкость, а
- суммарная емкость, а ![]() суммарное сопротивление
миелиновой оболочки. В силу первого закона Кирхгофа получаем:
суммарное сопротивление
миелиновой оболочки. В силу первого закона Кирхгофа получаем:
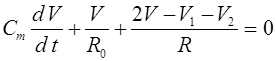 .
.
Для описания мембранных
потенциалов ![]() и
и ![]() перехватов служит уравнение
(6), в правую часть которого согласно закону Кирхгофа следует добавить для
левого перехвата слагаемое
перехватов служит уравнение
(6), в правую часть которого согласно закону Кирхгофа следует добавить для
левого перехвата слагаемое 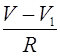 , а для
правого -слагаемое
, а для
правого -слагаемое 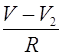 . Это токи,
проходящие между соответствующими перехватами и миелинизированным участком. В
результате получим уравнения:
. Это токи,
проходящие между соответствующими перехватами и миелинизированным участком. В
результате получим уравнения:
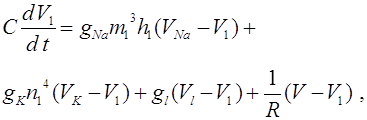
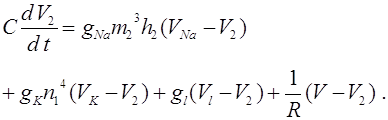
Величины ![]() ,
, ![]() и
и ![]()
![]() удовлетворяют
уравнениям (7) -(9), в которых для левого и правого перехватов следует положить
удовлетворяют
уравнениям (7) -(9), в которых для левого и правого перехватов следует положить
![]() и
и ![]() соответственно.
соответственно.
Структура и функции нейронов
Нервные клетки различаются
как по форме, так и по размерам. Существуют разные способы их классификации.
Один из важнейших критериев -наличие или отсутствие аксона. Знаменитый физиолог
Камилью Гольджи назвал нервные клетки с аксонами клетками типа ![]() , а без аксонов -типа
, а без аксонов -типа ![]() . Последние образуют лишь
локальные связи, т.е. только с непосредственно прилегающими к ним клетками.
Кроме нервных клеток в мозге присутствуют так называемые глиальные клетки. Их
число примерно в десять раз больше, чем нервных клеток, но их размеры в три
-четыре раза меньше, чем у нервных клеток. Глиальные клетки не генерируют
потенциалов действия. В настоящий момент считается, что они в целом выполняют
вспомогательные функции (некоторые из них хорошо изучены). Ниже будем говорить
о клетках типа
. Последние образуют лишь
локальные связи, т.е. только с непосредственно прилегающими к ним клетками.
Кроме нервных клеток в мозге присутствуют так называемые глиальные клетки. Их
число примерно в десять раз больше, чем нервных клеток, но их размеры в три
-четыре раза меньше, чем у нервных клеток. Глиальные клетки не генерируют
потенциалов действия. В настоящий момент считается, что они в целом выполняют
вспомогательные функции (некоторые из них хорошо изучены). Ниже будем говорить
о клетках типа ![]() . Именно их
будем называть нейронами.
. Именно их
будем называть нейронами.
В каждом нейроне различают
центральную часть -тело (оно же -сома) и отростки. Многочисленные, относительно
короткие, сильно ветвящиеся отростки называются дендритами. Они проводят
импульс, как правило, к телу нейрона. Единственный длинный отросток называется аксоном.
Он также сильно ветвится. Аксон проводит нервные импульсы от нейрона к другим
клеткам. Место отхождения аксона от тела называется аксонным холмиком. На
протяжении первых ![]() мкм. аксон не
имеет миелинового покрытия. Этот участок вместе с аксонным холмиком называется
начальным сегментом аксона. Последний значительно чувствительнее к воздействию,
чем остальные участки нейрона. Для возникновения потенциала действия достаточно
деполяризовать мембрану в начальном сегменте на
мкм. аксон не
имеет миелинового покрытия. Этот участок вместе с аксонным холмиком называется
начальным сегментом аксона. Последний значительно чувствительнее к воздействию,
чем остальные участки нейрона. Для возникновения потенциала действия достаточно
деполяризовать мембрану в начальном сегменте на ![]() мвт.
В теле клетки потенциал действия возникает при деполяризации мембраны на
мвт.
В теле клетки потенциал действия возникает при деполяризации мембраны на ![]() мв.
мв.
Разветвления аксона заканчиваются вблизи тел, дендритов и аксонов других нейронов. Места контактов Ч.Шерингтон назвал синапсами. По способу передачи возбуждения синапсы делятс на химические и электрические. Последние представляют собой участки непосредственного контакта мембран. Электрический импульс распросраняется через них в соответствии с законами электрических цепей ( проходят омический и емкостной токи).
Рассмотрим подробнее химические синапсы. Они различаются по своему местоположению: аксо -соматические, аксо- аксонные, аксо- дендритные (аксон заканчивается на соме, т.е. теле, аксоне, дендрите). Синапсы различаются по анатомической структуре, например, бывают пуговичные и шипиковые синапсы. В первом случае аксон заканчивается образованием похожим на пуговицу. Во втором - синапс напоминает кнопку, надетую на штырек (выступ мембраны нейрона). Несмотря на различия, химические синапсы объединяет ряд общих признаков и сам принцип функционирования.
Каждый синапс состоит из трех частей. Окончание аксона (пуговица, или “ кнопочка” для шипикового синапса) называется пресинаптической частью. Участок нейрона, на котором расположен контакт, называется постсинаптической частью. Эти части разделены синаптической щелью. В цитоплазме пресинаптической части постоянно накапливатся специльное вещество -медиатор, которое служит посредником при передаче воздействия. В результате спайка, пришедшего в пресинаптическую часть от нейрона -передатчика (пресинаптического нейрона), происходит выброс в синаптическую часть медиатора, заключенного в пузырьки. Количество выделившегося медиатора быстро нарастает, относительно стабилизируется, а затем медиатор распадается. Пересекая синаптическую щель, пузырьки достигают постсинаптической мембраны. Медиатор связывается с молекулами -рецепторами (запускается целый комплекс биохимических реакций). В постсинаптической мембране активируются специальные ионные каналы. Они называются медиатор -зависимыми. Происходит локальное изменение мембранного потенциала.
В открытом состоянии
медиатор -зависимым каналам отвечает свое равновесное значение мембранного
потенциала ![]() , которое называют
потенциалом реверсии. Для моделирования влияния открытых медиатор -зависимых
каналов в правую часть уравнения (6) Ходжкина -Хаксли следует добавить
слагаемое
, которое называют
потенциалом реверсии. Для моделирования влияния открытых медиатор -зависимых
каналов в правую часть уравнения (6) Ходжкина -Хаксли следует добавить
слагаемое ![]() , где
, где ![]() -коэффициент проводимости.
Если
-коэффициент проводимости.
Если ![]() , то значение локального
мембранного потенциала отклоняется в положительную сторону. Когда это отклонение
превышеет пороговое значение, запускаются механизмы генерации спайка. Если же
, то значение локального
мембранного потенциала отклоняется в положительную сторону. Когда это отклонение
превышеет пороговое значение, запускаются механизмы генерации спайка. Если же ![]() , то, наоборот, локальный
мембранный потенциал отклоняется в отрицательную сторону. Генерация спайка
затруднена.
, то, наоборот, локальный
мембранный потенциал отклоняется в отрицательную сторону. Генерация спайка
затруднена.
В первом случае говорят, что медиатор обладает возбуждающим, а во втором -тормозным действием. Аксон образует тысячи синапсов. Однако, в каждом из них выделяется один и тот же медиатор (правило Дейла). В этой связи нейроны делят на возбудительные и тормозные.
Следует сделать следующее
замечание. Выше потенциал реверсии отсчитывался от мембранного потенциала в
состоянии покоя, т.е. ![]() , где
, где ![]() -отклонение потенциала
реверсии от нуля,
-отклонение потенциала
реверсии от нуля, ![]() -аналогичное
отклонение потенциала покоя. Считается, что потенциал реверсии
-аналогичное
отклонение потенциала покоя. Считается, что потенциал реверсии ![]() для данного медиатора во
всех нейронах один и тот же. Однако, разные нейроны могут иметь различный
потенциал покоя
для данного медиатора во
всех нейронах один и тот же. Однако, разные нейроны могут иметь различный
потенциал покоя ![]() . Для одних
нейронов величина
. Для одних
нейронов величина ![]() может оказаться
положительной, а для других -отрицательной. Медиатор может оказывать как
возбуждающее, так и тормозное действие. Это явление наблюдается в природе. У
простейших набор медиаторов не велик. Один из самых распространенных -
ацетилхолин может быть как возбуждающим, так и тормозным медиатором.
может оказаться
положительной, а для других -отрицательной. Медиатор может оказывать как
возбуждающее, так и тормозное действие. Это явление наблюдается в природе. У
простейших набор медиаторов не велик. Один из самых распространенных -
ацетилхолин может быть как возбуждающим, так и тормозным медиатором.
На каждый синапс поступает импульс -сигнал “все, или ничего”. Однако, синапсы вносят разный вклад в суммарный мембранный потенциал. Он зависит от площади синаптического контакта, от количества медиатора, выделяющегося единовременно, а также от расположения синапса. Как уже говорилось, области, примыкающие к аксонному холмику, более чувствительны к воздействию. Влияние синапса на мембранный потенциал характеризуют синаптическим весом. Говорить о его числовом значении, естественно, можно только в рамках конкретной модели нейрона.
Отметим, что связь между нейронами посредством химических синапсов однонаправлена: возбуждение проводится от пресинаптического к постсинаптическому нейрону.
Синапсы обладают пластичностью. По экспериментальным данным синапс, часто принимающий участие в проведении возбуждения, увеличивается в размерах, а следовательно растет его влияние на постсинаптический нейрон (нейрон, на котором он расположен).
Еще одно важное свойство синаптического воздействия -явление рефрактерности (невосприимчивости к воздействию). О нем уже говорилось выше при описании гигантского аксона. Во время генерации спайка и некоторое время после него (это уже не бесспорно) постсинаптический нейрон не реагирует на воздействие медиатора. Данное явление называется абсолютной рефрактерностью, а соответствующий промежуток времени -периодом рефрактерности. Считается, что во время абсолютной рефрактерности никакое воздействие не способно индуцировать спайк нейрона. Постепенно абсолютная рефрактерность сменяется относительной. Достаточно сильное воздействие приводит с спайку. Затем способность реагировать на воздействие полностью восстанавливается.
Несмотря на малые размеры нейронов на каждом из них располагаются тысячи синапсов. Возбуждение, поступившее на синапс, вызывает локальное отклонение мембранного потенциала от состояния покоя. Как уже говорилось при описании гигантского аксона, эти локальные отклонения, если они не превышают пороговый уровень генерации спайка, “растекаются” по мембране, затухая как по пространству так и по времени. Чем дальше расположена точка от пропустившего воздействие синапса, тем меньше отклонение мембранного потенциала. Чем больше времени прошло с момента отклонения мембранного потенциала в зоне синаптического контакта, тем менее заметно возмущение мембранного потенциала в других точках.
Затухая, локальные отклонения складываются в зоне аксонного холмика. Если отклонение мембранного потенциала в зоне холмика превышает пороговое значение, то генерируется спайк, который распространяется по аксону. В случае, когда нейрон постоянно находится под интенсивным воздействием других нейронов, мембранный потенциал в зоне холмика часто превышает пороговое значение. На такое воздействие нейрон отвечает группой спайков -берстом. Промежутки между спайками не короче рефрактерного периода.
Тем самым, нейрон выполняет интегративные функции, суммируя поступающие к нему сигналы (импульсы) других нейронов (пространственное суммирование). Особеность суммирования заключается в том, что с течением времени результат воздействия накапливается (временное суммирование), но вклад каждого ранее поступившего импульса уменьшается. Нейрон генерирует битовый сигнал (импульс “все, или ничего”). Однако, частоту следования импульсов (или число импульсов в берсте) можно интерпретировать как аналоговый сигнал (точнее, его дискретное представление).
Потоки импульсов не являются
единственным фактором, действующим на нейроны. Между точками межклеточной
жидкости существует разность электрических потенциалов. Типичный объем, в
котором потенциал межклеточной жидкости можно считать практически постоянным
(местный потенциал), значительно превышает размеры нейрона. Местные потенциалы
колебательным образом меняются во времени. Это медленные потенциалы. Достаточно
типичный период их осциляций -порядка ![]() сек.
(напомним, для нейрона длительность импульса порядка
сек.
(напомним, для нейрона длительность импульса порядка ![]() мсек.). В изменение местных
потенциалов вносят вклад сами нервные клетки (не только нейроны), а также
омические токи, обусловленные электрическим градиентом во внеклеточной жидкости
(такая связь называется электротонической).
мсек.). В изменение местных
потенциалов вносят вклад сами нервные клетки (не только нейроны), а также
омические токи, обусловленные электрическим градиентом во внеклеточной жидкости
(такая связь называется электротонической).
Местные потенциалы влияют на
импульсацию нейронов. Этому есть доказательства. Изменение местных потенциалов
отражает сигнал электроэнцефалограммы (ЭЭГ), который регистрируется на
поверхности кожи, покрывающей череп. В спокойном состоянии у человека сигнал
ЭЭГ осцилирует с периодом порядка ![]() сек.
Замечено, что положительная полуволна ЭЭГ сопровождается учащением импульсации
нейронов. Тем самым, быстрые импульсные потенциалы наблюдаются на фоне и
связаны с медленными местными потенциалами. Механизмы связи и ее роль в целом в
настоящее время не ясны. По одной из гипотез именно постоянно меняющиеся узоры
местных потенциалов кодируют информацию в мозге. Потоки же импульсов служат для
передачи информационных сообщений из одной области мозга в другую.
сек.
Замечено, что положительная полуволна ЭЭГ сопровождается учащением импульсации
нейронов. Тем самым, быстрые импульсные потенциалы наблюдаются на фоне и
связаны с медленными местными потенциалами. Механизмы связи и ее роль в целом в
настоящее время не ясны. По одной из гипотез именно постоянно меняющиеся узоры
местных потенциалов кодируют информацию в мозге. Потоки же импульсов служат для
передачи информационных сообщений из одной области мозга в другую.
Однослойный персептрон - простейшая модель ассоциативной памяти
Однослойным персептроном
назовем множество нейронов Мак-Каллока - Питтса, которые имеют общие входы.
Пусть ![]() - входные сигналы, а
- входные сигналы, а ![]() - выходной сигнал
- выходной сигнал ![]() -ого нейрона,
-ого нейрона, ![]() , где
, где ![]() - число нейронов. Тогда
- число нейронов. Тогда
![]() .
.
Здесь ![]() - общий вектор входных
сигналов,
- общий вектор входных
сигналов, ![]() - синаптический вектор
- синаптический вектор ![]() - ого нейрона,
- ого нейрона, ![]() - его пороговое значение.
Выходные сигналы принимают либо нулевое, либо единичное значения (бинарны).
Предположения о бинарности вектора
- его пороговое значение.
Выходные сигналы принимают либо нулевое, либо единичное значения (бинарны).
Предположения о бинарности вектора ![]() делать не
будем. Персептрон формирует вектор выходных сигналов
делать не
будем. Персептрон формирует вектор выходных сигналов ![]() . Обозначим через
. Обозначим через ![]() - матрицу, в строках
которой находятся синаптические векторы
- матрицу, в строках
которой находятся синаптические векторы ![]() .
Ее назовем синаптической. Введем также вектор
.
Ее назовем синаптической. Введем также вектор ![]() ,
который назовем пороговым. Тогда выходной вектор персептрона суть
,
который назовем пороговым. Тогда выходной вектор персептрона суть
![]() ,
,
где функция ![]() вычисляется покоординатно.
Множество бинарных векторов (координаты равны либо нулю, либо единице)
обозначим через
вычисляется покоординатно.
Множество бинарных векторов (координаты равны либо нулю, либо единице)
обозначим через ![]() . Пусть
. Пусть ![]() - некоторый набор входных
векторов, а
- некоторый набор входных
векторов, а ![]() - множество выходных
векторов. Поставим задачу об обучении персептрона. Требуется выбрать
синаптическую матрицу
- множество выходных
векторов. Поставим задачу об обучении персептрона. Требуется выбрать
синаптическую матрицу ![]() и пороговый
вектор
и пороговый
вектор ![]() так, чтобы для входных
векторов
так, чтобы для входных
векторов ![]()
![]() персептрон
формировал выходные векторы
персептрон
формировал выходные векторы ![]() , т.е.
, т.е.
![]() .
.
Если обучение удалось
произвести, то персептрон выполняет функции ассоциативной памяти. По входному
вектору ![]() генерирует связанный с ним
выходной вектор
генерирует связанный с ним
выходной вектор ![]() . При этом если
входной вектор
. При этом если
входной вектор ![]() слегка искажен,
выходным вектором все равно будет вектор
слегка искажен,
выходным вектором все равно будет вектор ![]() (функция
(функция
![]() непрерывна). Часто пары
векторов
непрерывна). Часто пары
векторов ![]() называют ассоциативными
парами.
называют ассоциативными
парами.
Пусть ![]() и векторы
и векторы ![]() линейно независимы. Тогда
задача об обучении однослойного персептрона разрешимы. В силу того, что нейроны
слоя не связаны между собой, достаточно решить задачу обучения для
произвольного
линейно независимы. Тогда
задача об обучении однослойного персептрона разрешимы. В силу того, что нейроны
слоя не связаны между собой, достаточно решить задачу обучения для
произвольного ![]() -ого нейрона
(персептрон из одного нейрона). Его ассоциативные пары имеют вид:
-ого нейрона
(персептрон из одного нейрона). Его ассоциативные пары имеют вид: ![]()
![]() ,
где
,
где ![]() - координата с номером
- координата с номером ![]() вектора
вектора ![]() , которая принимает либо
нулевое, либо единичное значения. Таким образом, нейрон осуществляет
классификацию входных векторов: одним “ приписывает” нулевое, а другим -
единичное значения признака. Выше показано, что в рамках сделанных
предположений о векторах
, которая принимает либо
нулевое, либо единичное значения. Таким образом, нейрон осуществляет
классификацию входных векторов: одним “ приписывает” нулевое, а другим -
единичное значения признака. Выше показано, что в рамках сделанных
предположений о векторах ![]()
![]() задача классификации
разрешима. Описан алгоритм выбора синаптического вектора
задача классификации
разрешима. Описан алгоритм выбора синаптического вектора ![]() и порогового значения
и порогового значения ![]() , для которых
, для которых ![]() .
.
Задача об обучении
персептрона часто оказывается неразрешимой даже в простых случаях. Рассмотрим
персептрон, состоящий из одного нейрона, который имеет два синаптических входа,
т.е. входной вектор суть ![]() .
Поставим задачу найти синаптический вектор и пороговое значение такими, чтобы
для входных векторов
.
Поставим задачу найти синаптический вектор и пороговое значение такими, чтобы
для входных векторов ![]() и
и ![]() выходной сигнал был равен
единице, а для векторов
выходной сигнал был равен
единице, а для векторов ![]() и
и ![]() - нулю? Данный нейрон
должен реализовать логическую операцию “исключающее или”. Выпуклые оболочки
векторов
- нулю? Данный нейрон
должен реализовать логическую операцию “исключающее или”. Выпуклые оболочки
векторов ![]() и
и ![]() очевидно пересекаются в точке
очевидно пересекаются в точке
![]() . Следовательно,
поставленная задача в принципе не разрешима.
. Следовательно,
поставленная задача в принципе не разрешима.
Нерешенная простейшая задача
сильно уменьшает энтузиазм. Однако, оказывается, что она разрешима на
двухслойном персептроне. Рассмотрим конструкцию из трех нейронов. Первые два из
них имеют общие входы и образуют первый слой. Выходные сигналы этих нейронов
являются входными сигналами для третьего нейрона. Пусть ![]() и
и ![]() входной и выходной векторы
первого слоя, а
входной и выходной векторы
первого слоя, а ![]() - выходной
сигнал третьего нейрона. Положим для нейронов
- выходной
сигнал третьего нейрона. Положим для нейронов ![]() ,
,
![]() ,
, ![]() .Простым перебором
доказывается, что описанный персептрон реализует операцию “исключающее или”.
.Простым перебором
доказывается, что описанный персептрон реализует операцию “исключающее или”.
Рассмотренный пример -
решение задачи классификации на множестве бинарных векторов. Оказывается, что
теоретически двухслойный персептрон решает задачу классификации бинарных
векторов в общем случае. Однако, это утверждение имеет лишь теоретическое
значение, поскольку доказывается оно, когда число нейронов в первом слое равно ![]() , где
, где ![]() - размерность входного
вектора.
- размерность входного
вектора.