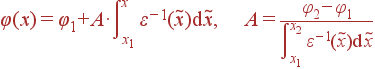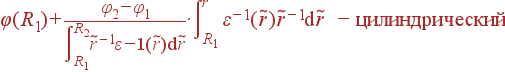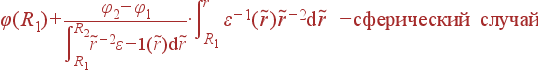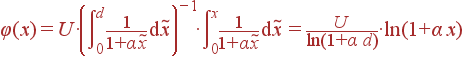Рефераты по рекламе
Рефераты по философии
Рефераты по финансам
Рефераты по химии
Рефераты по цифровым устройствам
Рефераты по экологическому праву
Рефераты по экономико-математическому моделированию
Рефераты по экономической географии
Рефераты по экономической теории
Рефераты по этике
Рефераты по юриспруденции
Рефераты по языковедению
Рефераты по юридическим наукам
Рефераты по истории
Рефераты по компьютерным наукам
Рефераты по медицинским наукам
Рефераты по финансовым наукам
Рефераты по управленческим наукам
Рефераты по строительным наукам
Психология педагогика
Промышленность производство
Биология и химия
Языкознание филология
Издательское дело и полиграфия
Рефераты по краеведению и этнографии
Рефераты по религии и мифологии
Рефераты по медицине
Рефераты по сексологии
Рефераты по москвоведению
Рефераты по экологии
Краткое содержание произведений
Рефераты по физкультуре и спорту
Топики по английскому языку
Рефераты по математике
Рефераты по музыке
Остальные рефераты
Статья: Расчет поля между эквипотенциальными поверхностями в неоднородной среде в отсутствие объемного заряда
Статья: Расчет поля между эквипотенциальными поверхностями в неоднородной среде в отсутствие объемного заряда
М.И. Векслер, Г.Г. Зегря
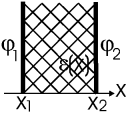
Это типичная ситуация в конденсаторе. Для ее рассмотрения используется уравнение Пуассона с ρ = 0, которое интегрируется с учетом условий φ(x1) = φ1, φ(x2) = φ2 (для плоскостного случая) или φ(r1) = φ1, φ(r2) = φ2 (сфера, цилиндр). Рассмотрим далее случай плоскости.
|
|
|
|
|
|
|
|
Далее можно дифференцированием по x найти поле Ex и Dx:
|
|
Следующий шаг - нахождение поляризованности и ее дивергенции, то есть связанного заряда ρ':
|
|
В точках разрыва ε(x) (на стыке двух диэлектриков) производная ε'(x) обращается в бесконечность, формула для ρ' cтановится неприменимой и надо искать поверхностный связанный заряд:
|
|
Обязательно проверяются условия на границах (в данном случае x1, x2) на наличие поверхностного связанного заряда:
|
|
В сферическом и цилиндрическом случаях надо правильно писать div в соответствующей системе координат. Выражения для φ(r) принимают вид:
| φ(r) | = |
|
|
| φ(r) | = |
|
после чего Er(r) и связанные заряды находятся аналогично тому, как это было сделано выше для плоскостного (декартового) случая.
Задача. Получить выражения для φ(r), Er(r), ρ ', σ ' в случае цилиндрической и сферической симметрии, если заданы зависимость ε(r), а также потенциалы граничных поверхностей φ(R1(2)) = φ1(2). ρ = 0.
Указание: Для промежуточной проверки использовать вышеприведенные выражения для потенциала.
Задача. Пространство между обкладками плоского конденсатора шириной d заполнено неоднородным диэлектриком c проницаемостью ε(x) = 1+α x. Найти φ(x), Ex(x), ρ ', σ ' на обкладках.
Решение: Будем считать, что конденсатор занимает область координат x = 0... d, причем потенциал одной обкладки (x = 0) равен φ1 = 0, а другой φ2 = U. Тогда зависимость потенциала от координаты находится как
|
|
после чего находим поле Ex(x) дифференцированием:
|
|
и далее получаем поляризованность Px:
|
|
Взяв дивергенцию, получаем объемный связанный заряд:
|
|
и еще проверяем условия на обкладках на наличие поверхностного заряда σ ':
| σ '|x = 0 | = | –Px|x = 0+ = 0 | |
| σ '|x = d | = |
|
Как и следовало ожидать, σ '|x = 0 = 0, поскольку у обкладки x = 0 диэлектрическая проницаемость равнa единице. Если U>0, то σ '|x = d<0, что тоже естественно: у обкладки x = d должен концентрироваться отрицательный связанный заряд. Для проверки найдем суммарный связанный заряд на единицу площали обкладки конденсатора - этот заряд должен оказаться равным нулю. Действительно,
|
|
= |
|
|
| = |
|
||
| = |
|
Список литературы
1. И.Е. Иродов, Задачи по общей физике, 3-е изд., М.: Издательство БИНОМ, 1998. - 448 с.; или 2-е изд., М.: Наука, 1988. - 416 с.
2. В.В. Батыгин, И.Н. Топтыгин, Сборник задач по электродинамике (под ред. М.М. Бредова), 2-е изд., М.: Наука, 1970. - 503 с.
3. Л.Д. Ландау, Е.М. Лифшиц, Теоретическая физика. т.8 Электродинамика сплошных сред, 2-е изд., М.: Наука, 1992. - 661 с.
Для подготовки данной работы были использованы материалы с сайта http://edu.ioffe.ru/r