
Рефераты по рекламе
Рефераты по философии
Рефераты по финансам
Рефераты по химии
Рефераты по цифровым устройствам
Рефераты по экологическому праву
Рефераты по экономико-математическому моделированию
Рефераты по экономической географии
Рефераты по экономической теории
Рефераты по этике
Рефераты по юриспруденции
Рефераты по языковедению
Рефераты по юридическим наукам
Рефераты по истории
Рефераты по компьютерным наукам
Рефераты по медицинским наукам
Рефераты по финансовым наукам
Рефераты по управленческим наукам
Рефераты по строительным наукам
Психология педагогика
Промышленность производство
Биология и химия
Языкознание филология
Издательское дело и полиграфия
Рефераты по краеведению и этнографии
Рефераты по религии и мифологии
Рефераты по медицине
Рефераты по сексологии
Рефераты по москвоведению
Рефераты по экологии
Краткое содержание произведений
Рефераты по физкультуре и спорту
Топики по английскому языку
Рефераты по математике
Рефераты по музыке
Остальные рефераты
Реферат: Поле. Примеры полей. Свойства полей. Поле рациональных чисел
Реферат: Поле. Примеры полей. Свойства полей. Поле рациональных чисел
Рассматривается определение поля, примеры и простейшие свойства полей, определения подполя, простого поля и поля рациональных чисел.
п.1. Определение поля.
Определение. Пусть ![]() - кольцо с единицей 1. Элемент
- кольцо с единицей 1. Элемент ![]() из множества
из множества ![]() называется
обратным в кольце
называется
обратным в кольце ![]() , если
, если ![]()
![]() .
. ![]() называется обратным к
называется обратным к ![]() .
.
Примеры.
Рассмотрим кольцо целых чисел, то есть кольцо ![]() , элемент 2
необратим в этом кольце, так как
, элемент 2
необратим в этом кольце, так как ![]() , элемент 5 необратим в кольце
целых чисел.
, элемент 5 необратим в кольце
целых чисел. ![]() - обратимые элементы в кольце
целых чисел
- обратимые элементы в кольце
целых чисел
Рассмотрим кольцо рациональных чисел ![]() , обратимыми являются
все элементы кроме
, обратимыми являются
все элементы кроме ![]() .
.
Рассмотрим кольцо действительных чисел, то есть кольцо
![]() ,
обратимыми являются все элементы кроме
,
обратимыми являются все элементы кроме ![]() .
.
Определение. Поле – это кольцо ![]() , если:
, если:
![]() - коммутативное кольцо (операция
- коммутативное кольцо (операция ![]() коммутативна)
коммутативна)
![]() - кольцо с единицей 1, единица
- кольцо с единицей 1, единица ![]() .
.
Всякий ненулевой элемент кольца ![]() обратим.
обратим.
Примеры полей.
![]() - поле рациональных чисел.
- поле рациональных чисел.
![]() - поле действительных чисел.
- поле действительных чисел.
Это поля с бесконечным числом элементов. Рассмотрим поле с конечным числом элементов.
Поле Галуа ![]() - галуафилд.
- галуафилд. ![]() ;
; ![]() . Определим
. Определим
операции сложения и умножения:
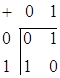 И
И 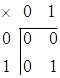
![]()
![]() - бинарные операции,
- бинарные операции, ![]() - унарная
- унарная
Из этой таблицы видно, что операция ![]() - коммутативна,
- коммутативна, ![]() -бинарные
операции,
-бинарные
операции, ![]() -
унарная операция, т.к.
-
унарная операция, т.к. ![]() ,
, ![]() .
.
п.2. Простейшие свойства поля.
Пусть ![]() - поле. Обозначение:
- поле. Обозначение: ![]()
![]()
![]()
![]() .
.
Если ![]() , то
, то ![]() .
.
Доказательство. Пусть ![]() , докажем, что
, докажем, что ![]() , то есть
, то есть ![]() , тогда
, тогда ![]() противоречие с аксиомой
поля
противоречие с аксиомой
поля ![]()
![]() . Если
. Если ![]() , то по аксиоме
полей
, то по аксиоме
полей ![]()
![]() |
| ![]() ,
, ![]()
![]() .
.
Если ![]() ,
, ![]() .
. ![]() умножим равенство
умножим равенство ![]() справа на
справа на ![]() , то есть
, то есть ![]()
![]() .
.
![]() .
.
Доказательство. Если ![]() , то
, то ![]()
![]() , умножая обе части равенства
, умножая обе части равенства ![]() на
на ![]() слева,
слева, ![]()
![]() .
.
В поле нет делителей 0.
Доказательство. Следует из свойства 3, применяя законы
контрапозиции: ![]() ,
, ![]()
![]()
![]() , значит нет делителей нуля.
, значит нет делителей нуля.
Каждое поле является областью целостности.
Доказательство. Следует из определения поля и области целостности.
![]() .
.
Доказательство. ![]()
![]() . Умножим обе части равенства
справа на
. Умножим обе части равенства
справа на ![]()
![]() , где
, где ![]() .
.
![]() , где
, где ![]() .
.
Доказательство. Выпишем правую часть ![]()
![]()
![]() равна левой части.
равна левой части.
![]() , где
, где ![]() .
.
Доказательство. Правая часть ![]()
![]()
![]() равна левой части.
равна левой части.
![]() ,
, ![]() .
.
Доказательство. Правая часть ![]()
![]()
![]() левая часть.
левая часть.
![]() ,
, ![]() .
.
Доказательство. Левая часть ![]()
![]() .
.
![]() ,
, ![]() .
.
Если ![]() , то
, то ![]() .
.
Доказательство. Вычислим произведение ![]()
![]()
![]()
![]() то есть
то есть ![]() обратный элемент к
обратный элемент к ![]() .
.
![]() , где
, где ![]() .
.
Доказательство. Левая часть равна ![]()
![]() равна правой части.
равна правой части.
![]() - коммутативная группа, которая
называется мультипликативной группой не равных 0 элементов.
- коммутативная группа, которая
называется мультипликативной группой не равных 0 элементов.
Доказательство. Следует из свойств поля: ![]()
1. ![]() , так как поле.
, так как поле.
2. ![]()
3. ![]()
4. ![]() , так как поле
, так как поле
Так как поле – это кольцо определённого вида, то под гомоморфизмами полей понимаются гомоморфизмы полей. Аналогично для изоморфизмов.
Определение. Подполем поля ![]() называется подкольцом с единицей
поля
называется подкольцом с единицей
поля ![]() , в
котором всякий ненулевой элемент обратим. Всякое подполе является полем.
Подполе поля
, в
котором всякий ненулевой элемент обратим. Всякое подполе является полем.
Подполе поля ![]() , отличное от
, отличное от ![]() называется собственным
полем.
называется собственным
полем.
Определение. Поле называется простым, если оно не имеет собственных подполей.
Пример. Рассмотрим поле действительных чисел, то есть
поле ![]() .
Для того, чтобы найти подполе надо найти подмножества замкнутые относительно
операции
.
Для того, чтобы найти подполе надо найти подмножества замкнутые относительно
операции ![]() и
и
![]()
![]() подмножеству.
Например, поле рациональных чисел является подполем поля действительных чисел.
подмножеству.
Например, поле рациональных чисел является подполем поля действительных чисел.
Алгебраическая система ![]() называется системой рациональных
чисел, если:
называется системой рациональных
чисел, если:
Алгебра ![]() - это поле с единицей 1.
- это поле с единицей 1.
Множество ![]() замкнуто относительно операции
замкнуто относительно операции ![]() и
и ![]()
Аксиома минимальности, если ![]() такое, что:
такое, что:
а) ![]()
б) ![]()
![]() , тогда
, тогда ![]() .
.
Список литературы
Е.Е. Маренич, А.С. Маренич. Вводный курс математики. Учебно-методическое пособие. 2002
В.Е. Маренич. Журнал «Аргумент». Задачи по теории групп.
Кострикин А.И. Введение в алгебру. Ч.1 Основы алгебры. – М.: Физмат лит-ра, 2000
Кострикин А.И. Введение в алгебру. Ч.2 Основы алгебры. – М.: Физмат лит-ра, 2000
Кострикин А.И. Введение в алгебру. Ч.3 Основные структуры алгебры. – М.: Физмат лит-ра, 2000
Кострикин А.И. Сборник задач по алгебре. Изд. третье – М.: Физмат лит-ра, 2001
Для подготовки данной работы были использованы материалы с сайта http://referat.ru/