
Рефераты по рекламе
Рефераты по философии
Рефераты по финансам
Рефераты по химии
Рефераты по цифровым устройствам
Рефераты по экологическому праву
Рефераты по экономико-математическому моделированию
Рефераты по экономической географии
Рефераты по экономической теории
Рефераты по этике
Рефераты по юриспруденции
Рефераты по языковедению
Рефераты по юридическим наукам
Рефераты по истории
Рефераты по компьютерным наукам
Рефераты по медицинским наукам
Рефераты по финансовым наукам
Рефераты по управленческим наукам
Рефераты по строительным наукам
Психология педагогика
Промышленность производство
Биология и химия
Языкознание филология
Издательское дело и полиграфия
Рефераты по краеведению и этнографии
Рефераты по религии и мифологии
Рефераты по медицине
Рефераты по сексологии
Рефераты по москвоведению
Рефераты по экологии
Краткое содержание произведений
Рефераты по физкультуре и спорту
Топики по английскому языку
Рефераты по математике
Рефераты по музыке
Остальные рефераты
Реферат: Перестановки
Реферат: Перестановки
Описываются понятия r-перестановок множества, r-сочетания, перестановки с повторениями.
п.1. r- перестановки.
Определение. r- перестановкой множества A называется кортеж из r попарно различных элементов множества A. Иногда r- перестановки называют размещениями без повторения.
Если (a![]() , ..., a
, ..., a![]() ) есть r- перестановка n-
элементного множества, то r £ n.
) есть r- перестановка n-
элементного множества, то r £ n.
Обозначение. Обозначим P(n, r) число всех r- перестановок n- элементного множества, где n, rÎN. Положим P(n, 0) = 1 для nÎN0.
Теорема 1. Число всех r- перестановок n- элементного множества, где
n, rÎN, вычисляется по формуле
P(n, r) = n![]() = n(n -1)...(n - r + 1). (1)
= n(n -1)...(n - r + 1). (1)
Доказательство. Первая координата r- перестановки n- элементного множества может быть выбрана n способами, если первая координата выбрана, то вторая координата может быть выбрана n-1 способами, если выбраны первые две координаты, то третья координата может быть выбрана n-2 способами и т.д. до r- ой координаты включительно, которая может быть выбрана n-r+1 способами. Из теоремы 2, п.3, следует равенство (1).
Следствие 1. Пусть A и B- конечные множества, |A| = n, |B| = r, где
n, r ÎN. Тогда число всех
инъекций f: B ® A равно P(n, r) = n![]() .
.
Доказательство. Обозначим B={b![]() , ..., b
, ..., b![]() }, инъекция f: B ®A может быть записана в табличной форме
}, инъекция f: B ®A может быть записана в табличной форме
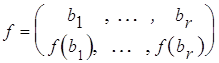 ,
,
где кортеж ![]() есть r- перестановка множества A.
Поэтому искомое число равно P(n, r).
есть r- перестановка множества A.
Поэтому искомое число равно P(n, r).
Определение. Пусть A есть n- элементное множество. Перестановкой множества A называется n- перестановка множества A. Другими словами, перестановка множества A это кортеж содержащий все элементы множества A по одному разу.
Следствие 2. Число всех перестановок n- элементного множества равно n!.
Доказательство. Искомое число равно P(n, n) = n![]() =
n(n-1)...(n-n+1) =
=
n(n-1)...(n-n+1) =
= n!.
Следствие 3. Пусть A и B- конечные множества, |A| = |B| = n, nÎN. Тогда число всех биекций f: B ® A равно n!.
Доказательство. Т.к. |A| = |B|, то каждая биекция f: B ® A является инъекцией и наоборот. По следствию 1, искомое число равно P(n, n) = n!.
п.2. r -элементные подмножества (r - сочетания).
Определение. Пусть A- конечное множество. r- сочетанием множества A называется любое r- элементное подмножество множества A.
Теорема 1. Пусть A есть n- элементное множество, n, rÎN![]() . Справедливы утверждения:
. Справедливы утверждения:
1. Число всех r- сочетаний n- элементного множества
равно ![]() .
.
2. Число всех r- элементных подмножеств n- элементного
множества равно ![]() .
.
Доказательство. Обозначим K- число всех r- сочетаний
n- элементного множества A. Каждое r- элементное подмножество n- элементного
множества A определяет r! перестановок множества A, при этом разные
подмножества определяют разные перестановки. Поэтому K×r! - число всех r- перестановок множества A, равное n![]() . Отсюда
следует, что K = n
. Отсюда
следует, что K = n![]() / r! = =
/ r! = =![]() .
.
Пример 1. Каждый кортеж ![]() N
N![]() , где
, где ![]() , кодируется k-элементным
подмножеством
, кодируется k-элементным
подмножеством ![]() множества
множества ![]() . Поэтому, при
фиксированном k, число всех кортежей
. Поэтому, при
фиксированном k, число всех кортежей ![]() N
N![]() , где
, где ![]() , равно
, равно ![]() .
.
Пример 2. Перечисление беспорядков степени n.
Обозначим U- множество всех перестановок степени n, ![]() . Будем считать, что элементами
перестановок являются числа
. Будем считать, что элементами
перестановок являются числа ![]() . Перестановка
. Перестановка ![]() степени n называется
беспорядком, если
степени n называется
беспорядком, если ![]() для всех
для всех ![]() .
.
Существует только один беспорядок ![]() степени 2.
степени 2.
Существует только два беспорядка ![]() степени 3.
степени 3.
Для ![]() обозначим
обозначим ![]() множество всех
множество всех ![]() перестановок
степени n таких, что
перестановок
степени n таких, что ![]() . Число всех беспорядков степени n
равно числу всех перестановок степени n не принадлежащих множеству
. Число всех беспорядков степени n
равно числу всех перестановок степени n не принадлежащих множеству ![]() . Обозначим
. Обозначим ![]() число всех
беспорядков степени n. По формуле включения- исключения
число всех
беспорядков степени n. По формуле включения- исключения
![]() , (1)
, (1)
где суммирование ведётся по всем кортежам ![]() N
N![]() таким, что
таким, что
![]() . Легко видеть, что для любого
кортежа
. Легко видеть, что для любого
кортежа ![]() N
N![]() , где
, где ![]() справедливо
равенство
справедливо
равенство
![]() .
.
При фиксированном k число всех кортежей ![]() N
N![]() , где
, где ![]() , равно
, равно ![]() . Из равенства (1)
следует, что
. Из равенства (1)
следует, что
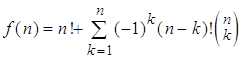 .
.
Поэтому
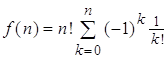 .
.
п.3. Перестановки с повторениями.
Определение. Кортеж t = (b![]() , ..., b
, ..., b![]() ) называется
перестановкой с повторениями состава (n
) называется
перестановкой с повторениями состава (n![]() , ..., n
, ..., n![]() ) множества {a
) множества {a![]() , ..., a
, ..., a![]() }, если элемент a
}, если элемент a![]() входит в t n
входит в t n![]() раз, ..., a
раз, ..., a![]() входит в t n
входит в t n![]() раз, где n
раз, где n![]() , ..., n
, ..., n![]() ÎN
ÎN![]() ,
, ![]() .
.
Обозначение. Обозначим P(n![]() , ..., n
, ..., n![]() ) число всех перестановок с
повторениями состава (n
) число всех перестановок с
повторениями состава (n![]() , ..., n
, ..., n![]() ) некоторого k - элементного
множества, где n = = n
) некоторого k - элементного
множества, где n = = n![]() +...+n
+...+n![]() .
.
Теорема 1. Для любого (n![]() , ..., n
, ..., n![]() )ÎN
)ÎN![]()
P(n![]() , ..., n
, ..., n![]() ) = n!/n
) = n!/n![]() !...n
!...n![]() ! , где n = n
! , где n = n![]() +...+n
+...+n![]() .
.
Доказательство. Перестановка (b![]() , ..., b
, ..., b![]() ) состава (n
) состава (n![]() , ..., n
, ..., n![]() ) множества {a
) множества {a![]() , ..., a
, ..., a![]() } кодируется
кортежем длины k: на первом месте кортежа записано множество тех мест в
перестановке на которых расположен элемент
} кодируется
кортежем длины k: на первом месте кортежа записано множество тех мест в
перестановке на которых расположен элемент ![]() ; на втором месте кортежа записано
множество тех мест в перестановке, на которых расположен элемент
; на втором месте кортежа записано
множество тех мест в перестановке, на которых расположен элемент ![]() ; ...; на k - ом месте
кортежа записано множество тех мест в перестановке, на которых расположен
элемент
; ...; на k - ом месте
кортежа записано множество тех мест в перестановке, на которых расположен
элемент ![]() .
Первый элемент кортежа может быть выбран
.
Первый элемент кортежа может быть выбран ![]() способами; если первый элемент
выбран, то второй можно выбрать
способами; если первый элемент
выбран, то второй можно выбрать 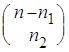 способами; ...; если первые
способами; ...; если первые ![]() элементов
выбраны, то k- ый элемент может быть выбран
элементов
выбраны, то k- ый элемент может быть выбран 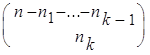 способами. По правилу произведения
получаем, что число всех перестановок с повторениями состава (n
способами. По правилу произведения
получаем, что число всех перестановок с повторениями состава (n![]() , ..., n
, ..., n![]() ) из {a
) из {a![]() , ..., a
, ..., a![]() } равно
} равно
P(n![]() , ..., n
, ..., n![]() ) =
) = ![]()
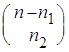 ...
...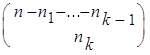 =
=
= 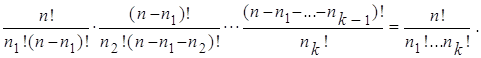
Обозначение. Для " n![]() , ..., n
, ..., n![]() ÎN
ÎN![]() полиномиальный коэффициент
полиномиальный коэффициент 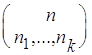 определяется
равенствами:
определяется
равенствами:
если n![]() +...+ n
+...+ n![]() = n, то
= n, то 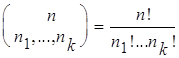 ;
;
если n![]() +...+ n
+...+ n![]() ¹ n, то
¹ n, то 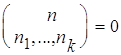 .
.
Следствие 1. Пусть A и B- конечные множества такие,
что |A| = n, |B| = k, (n![]() , ..., n
, ..., n![]() )ÎN
)ÎN![]() , n
, n![]() +...+ n
+...+ n![]() = n, B = {b
= n, B = {b![]() , ..., b
, ..., b![]() }. Тогда число
всех функций
}. Тогда число
всех функций
f: A ® B таких, что |f ![]() (b
(b![]() )| = n
)| = n![]() для всех i = 1, ..., k, равно
для всех i = 1, ..., k, равно 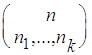 .
.
Доказательство. Пусть A={a![]() , ..., a
, ..., a![]() }. Запишем функцию f: A ® B в табличном
виде
}. Запишем функцию f: A ® B в табличном
виде 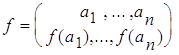 .
.
Кортеж (f(a![]() ), ..., f(a
), ..., f(a![]() )) есть перестановка с
повторениями состава (n
)) есть перестановка с
повторениями состава (n![]() , ..., n
, ..., n![]() ) множества {b
) множества {b![]() , ..., b
, ..., b![]() }.
}.
Следствие 2. Пусть U- конечное множество, |U| = n.
Тогда число кортежей множеств (A![]() , ..., A
, ..., A![]() ) таких, что
) таких, что
|A![]() | = n
| = n![]() , ..., |A
, ..., |A![]() | = n
| = n![]() ,
,
|A![]() ÇA
ÇA![]() | = Æ для всех i ¹ j,
| = Æ для всех i ¹ j,
A![]() È...ÈA
È...ÈA![]() = U, равно
= U, равно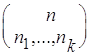 .
.
Доказательство. По теореме 2 п.3 число таких кортежей равно
![]()
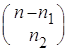 ...
...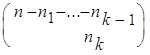 =
= 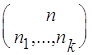 .
.
Список литературы
Е.Е. Маренич, А.С. Маренич. Вводный курс математики. Учебно-методическое пособие. 2002
В.Е. Маренич. Журнал «Аргумент». Задачи по теории групп.
Кострикин А.И. Введение в алгебру. Ч.1 Основы алгебры. – М.: Физмат лит-ра, 2000
Кострикин А.И. Введение в алгебру. Ч.2 Основы алгебры. – М.: Физмат лит-ра, 2000
Кострикин А.И. Введение в алгебру. Ч.3 Основные структуры алгебры. – М.: Физмат лит-ра, 2000
Кострикин А.И. Сборник задач по алгебре. Изд. третье – М.: Физмат лит-ра, 2001
Для подготовки данной работы были использованы материалы с сайта http://referat.ru/