Реферат: Кольца. Примеры колец. Гомоморфизмы и изоморфизмы колец. Подкольца. Кольцо целых чисел

Для изучения предлагаются понятия кольца, коммутативного кольца и области целосности, гомоморфизма и изоморфизма колец, подкольца, а так же свойства кольца целых чисел.

п.1. Понятие кольца.

Определение. Алгебра , где - бинарные операции, - унарная операция, называется кольцом, если выполнены аксиомы.

I. - абелева группа.

II. 1) - ассоциативность умножения.

2) законы дистрибутивности: - левый дистрибутивный закон, - правый дистрибутивный закон.

- называется аддитивной группой кольца.

Определение. Кольцо называется кольцом с единицей , если существует

Определение. Кольцо называется коммутативным, если

Определение. Элементы называются делителями , если

Определение. Кольцо называется областью целостности, если оно обладает свойствами:

Кольцо - коммутативно.

Кольцо с единицей , где .

Кольцо не имеет делителей нуля.

п.2. Примеры колец.

Рассмотрим . Операции - бинарная операция на множестве , операция - унарная операция на множестве , , значит - алгебра. Аксиомы кольца на множестве выполнены, это следует из свойств целых чисел, значит - кольцо. Это кольцо с единицей 1, так как и . Это коммутативное кольцо, так как . Это кольцо без делителей нуля. Кольцо целых чисел является областью целостности.

Пусть - множество целых чётных чисел, - алгебра, кольцо без единицы, коммутативное, без делителей нуля, не является областью целостности.

- проверим, будет ли на множестве - кольцо.

- бинарная операция на множестве .

- унарная операция на множестве .

Значит - алгебра.

Аксиомы кольца для данной алгебры выполнены, так как , а на аксиомы выполнены (из свойств действительных чисел), значит - это кольцо.

. . Кольцо с единицей - это коммутативное кольцо без делителей нуля, является областью целостности.

Пусть . Определим операции , ; , .

- бинарные операции на множестве

значит - унарная операция на множестве .

, , значит - алгебра. Проверим, является ли эта алгебра кольцом. Для этого проверим аксиомы кольца. Равенство - равенство функции: из определения операций. Рассмотрим произведение , вычислим значения левой и правой частей от а) б) . Аналогично проверяется, что все аксиомы кольца выполнены, значит является кольцом. Это кольцо с единицей . Действительно, (свойство единицы). Это коммутативное кольцо, так как . Покажем, что это кольцо с делителями нуля. Пусть , , , (нулевая функция). Вычислим (равно нулевой функции). Значит , - делители нуля, значит кольцо - не является областью целостности.

п.3. Простейшие свойства кольца.

Пусть - кольцо. Выпишем и проверим аксиомы кольца:

Доказательство. - абелева группа, имеем

Доказательство. - абелева группа, имеем .

, если , если .

Доказательство. По закону сокращения в группе, определенной на множестве .

, если , если .

Доказательство. Следует из свойства 4 групп.

если , если .

Доказательство. Следует из 5 свойства групп.

Доказательство. Следует из 6 свойства групп.

Доказательство. Докажем, что .

Доказательство. Докажем, что рассмотрим сумму . Аналогично доказывается, что .

. Обозначение: .

(правый дистрибутивный закон), (левый дистрибутивный закон).

Доказательство. Правый дистрибутивный закон: левая часть равна равна правой части. Аналогично доказывается левый дистрибутивный закон.

Доказательство. Вычислим сумму .

п.4. Гомоморфизмы и изоморфизмы колец.

Дано два кольца и .

Определение. Гомоморфизмом кольца в кольце называется функция и обладающая свойствами:

Другими словами, гомоморфизм колец – это отображения, сохраняющие все операции кольца. Если - гомоморфизм кольца в , то - гомоморфизм абелевых групп в группу .

Теорема. Пусть и - кольца и , обладающих свойствами:

Тогда - гомоморфизм колец.

Доказательство. Из свойства является гомоморфизмом групп и , поэтому обладает свойствами: , , значит по определению - гомоморфизм колец.

Определение. Отображение называется изоморфизмом кольца на , если обладает свойствами:

- гомоморфизм колец.

- биекция.

Другими словами: изоморфизм – это гомоморфизм, являющийся биекцией.

п.5. Подкольца.

Пусть - кольцо, , .

Определение. Множество - замкнуто относительно операции , если .

Множество - замкнуто относительно операции , если . Множество - замкнуто относительно операции , если .

Теорема. Пусть - кольцо, , , если - замкнуто относительно операции , то - кольцо, которое называется подкольцом, кольца .

Доказательство. - бинарные операции, - унарная операция, так как - замкнутое множество. Так как , то существует , так как - замкнуто относительно операции , то , значит - алгебра, так как аксиомы выполнены на , то они выполнены и на , потому алгебра - кольцо.

Теорема. Пусть - числовое кольцо с единицей 1, тогда оно содержит подкольцо целых чисел.

п.6. Аксиоматическое определение кольца целых чисел.

Алгебраическая система , где бинарные операции, - унарная операция, , , называется системой целых чисел, если выполнены три группы аксиом:

I. - кольцо.

Абелева группа

Аддитивная группа

II. Множество - замкнуто относительно операций и алгебраическая система является системой натуральных чисел (системой Пеано).

Для ,

Аксиома индукции: пусть . Если множество удовлетворяет условиям:

а)

б) , , то

III. Аксиома минимальности.

Если и обладает свойствами:

а)

б) , то .

Свойства целых чисел.

Теорема 1. О делении с остатком.

| , где . Число называется делимым, - делителем, - частным, - остатком при делении на .

Доказательство. Докажем существование хотя бы одной пары чисел , . Для этого рассмотрим множество . Множество содержит как отрицательные, так и неотрицательные числа, пусть - наименьшее неотрицательное число в , тогда . Докажем, что , предположим противное . Рассмотрим число . противоречие с выбором . Доказано, что , . Докажем единственность чисел и , пусть . , . Докажем, что , предположим противное . Пусть . Имеем 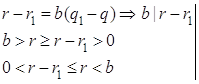противоречие, так как между числами нет чисел, делящихся на . Доказано, что , если , то , а отсюда следует, что . Доказана единственность чисел и .