Реферат: Интеграл по комплексной переменной

Реферат: Интеграл по комплексной переменной

Определение 1: Кривая Г называется гладкой ,если она имеет непрерывно изменяющуюся касательную.

Определение 2: Кривая называется кусочно-гладкой ,если она состоит из конечного числа гладких дуг.

Основные свойства : Пусть на комплексной плоскости  Z задана кусочно-гладкая кривая С длиной  l, используя  параметрическое задание кривой С зададим h(t) и x (t), где h и x являются кусочно-гладкими кривыми от действительной  переменной t. Пусть a t i.

Dz i =z i – z i-1. Составим интегрируемую функцию S = åf (z*)Dz i .  (1)
где z*– производная точки этой дуги.

Если при стремлении max |Dz i |® 0 существует предел частных сумм не зависящий ни от способа разбиения кривой С на частичные дуги, ни от выбора точек z i , то этот  предел называется интегралом от функции f (z ) по кривой С.

                            (2) 

f (zi* ) = u (Pi*) + iv (Pi*)      (3)

где Dz i = Dx (t) + iDh(t)     (x (t) и h(t) - действительные числа)

Подставив (3) в (1) получим :

           (4)

Очевидно, что (4) состоит из суммы двух частных сумм, криволинейных интегралов действительной переменной. Переходя в (4) к пределу при Dx и Dh ® 0 и предполагая, что данные пределы существуют, получаем :

                                                            (5)

Заметим, что для существования криволинейного интегралов, входящих в (5), а тем самым и для существования интеграла (2) достаточно кусочной непрерывности функций u и v. Это означает, что (2) существует и в случае неаналитичности функции f (z ).

Сформулируем некоторые свойства интеграла от функции комплексной переменной. Из равенства (5) следуют свойства :

О ограниченности интеграла.

   7.) Пусть Cp – окружность радиуса r, с центром в точке Z0. Обход вокруг контура Cp осуществляется против часовой стрелки. Cp : z = Z0 + r×eij,    0 £ j £ 2p,      dz = ir×eij dj .

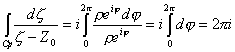
Кусочно-гладкую замкнутую кривую будем называть замкнутым контуром, а интеграл по замкнутому контуру – контурным интегралом.

ТЕОРЕМА КОШИ.

В качестве положительного обхода контура выберем направление при котором внутренняя область, ограниченная данным замкнутым контуром остается слева от направления движения :

Для действительной переменной имеют место формулы Грина. Известно, что если функции P(x, y) и Q(x, y) являются непрерывными в некоторой заданной области G, ограниченны кусочно-гладкой кривой С, а их частные производные 1-го порядка непрерывны в G, то имеет место формула Грина:

        ( 8 )

ТЕОРЕМА : Пусть в односвязной области G задана аналитическая функция f(Z), тогда интеграл от этой функции по замкнутому контуру Г целиком лежащему в G , равен нулю.

Доказательство : из формулы (5) следует:

Т.к. f(z ) аналитическая всюду, то  U(x, y), V(x, y) - непрерывны в области, ограниченной этим контуром и при этом выполняются условия Коши-Римана. Используя свойство криволинейных интегралов:

Аналогично :

По условию Коши-Римана в последних равенствах скобки равны нулю, а значит и оба криволинейных интеграла равны нулю. Отсюда :

ТЕОРЕМА 2 (Вторая формулировка теоремы Коши) : Если функция f(z) является аналитической в односвязной области G, ограниченной кусочно-гладким контуром C, и непрерывна в замкнутой области G, то интеграл от такой функции по границе С области G равен нулю.

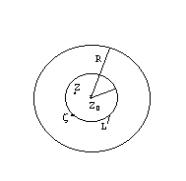
TEOPEMA 3 (Расширение теоремы Коши на многосвязную область) :

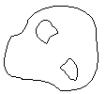Пусть f (z) является аналитической функцией в многосвязной области G, ограниченной извне контуром С0, а изнутри контурами С1, С2, .. ,Сn (см. рис.). Пусть f (z) непрерывна в замкнутой области G, тогда :

, где С – полная граница области G, состоящая из контуров С1, С2, .. , Сn. Причем обход кривой С осуществляется в положительном направлении.

Неопределенный интеграл.

 интеграл по какой-либо кривой, целиком лежащей в области G, содержащей Z0 и Z, в силу теории Коши этот интеграл не зависит от выбора кривой интегрирования и является однозначной функцией  Ф(Z). Аналитическая функция Ф(Z) называется первообразной от функции f(Z) в области G, если в этой области имеет место равенство : Ф¢ (Z) = f( Z).

Определение: Совокупность всех первообразных называется неопределенным интегралом от комплексной функции f(Z). Так же как и в случае с функцией действительного переменного имеет место равенство :

                  ( 9)

Это аналог формулы Ньютона-Лейбница.

Интеграл Коши. Вывод формулы Коши.

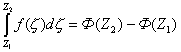Ранее была сформулирована теорема Коши, которая позволяет установить связь между значениями аналитической функции во внутренних точках области ее аналитичности и граничными значениями этой функции.

По свойствам интегралов :

          (2 )

Так как левый интеграл в (2) не зависит от выбора контура интегрирования, то и правый интеграл также не будет зависеть от выбора контура. Выберем в качестве g окружность gr с радиусом r . Тогда:

           (3)

Уравнение окружности gr : z = Z0 + reij         (4)

Подставив (4) в (3) получим :

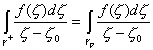
       ( 5 )

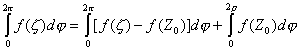
            ( 6 )

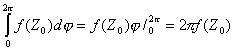
       (7)

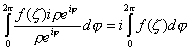Устремим  gr® 0, т.е. r® 0.

Тогда т.к. функция  f(z) аналитична в точке Z=Z0 и всюду в области G, а следовательно и непрерывна в G, то для всех e>0 существует r>0, что для всех z из r–окрестности точки Z0 выполняется | f(z) – f(Z0) | < e.>

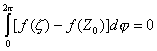
               (8)

Подставив ( 7) в ( 6) с учетом ( 8) получаем :

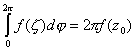
Подставляя в ( 5)  и выражая f(Z0) имеем :

            (9)

Это интеграл Коши.

Интеграл, стоящий в (9) в правой части выражает значение аналитической функции f(z) в некоторой точке Z0 через ее значение на произвольном контуре g , лежащем в области аналитичности функции f(z) и содержащем точку Z0 внутри.

Очевидно, что если бы функция f(z) была аналитична и в точках контура С, то в качестве границы g в формуле (9) можно было использовать контур С.

Приведенные рассуждения остаются справедливыми и в случае многосвязной области G.

Следствие : Интеграл Коши, целиком принадлежащий аналитической области G имеет смысл для любого положения Z0 на комплексной плоскости при условии, что эта точка есть внутренней точкой области Г. При этом если Z0 принадлежит области с границей Г, то значение интеграла равно (9), а если т. Z0 принадлежит внешней области, то интеграл равен нулю :

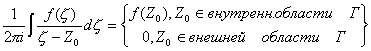
При Z0 Î Г указанный интеграл не существует.

Интегралы, зависящие от параметра.

Рассматривая интеграл Коши, видим, что подинтегральная функция зависит от 2-х комплексных переменных : переменной интегрирования z и Z0. Таким образом интеграл Коши может быть рассмотрен как интеграл, зависящий от параметра, в качестве которого выбираем точку Z0.

Пусть задана функция двух комплексных переменных j (Z, z ), причем   Z= x + iy  в точке, принадлежащей некоторой комплексной плоскости G. z= x+ ih  Î  С.  (С - граница G).

Взаимное расположение области и кривой произвольно. Пусть функция j (Z, z )  удовлетворяет условиям : 1) Функция для всех значений z Î  С является аналитической в области G. 2) Функция j (Z, z )  и ее производная ¶j/¶Z являются непрерывными функциями по совокупности переменных Z и z при произвольном изменении области G и переменных на кривой С. Очевидно, что при сделанных предположениях :

Интеграл существует и является функцией комплексной переменной. Справедлива формула :

                              (2)

Эта формула устанавливает возможность вычисления производной от исходного интеграла путем дифференцирования подинтегральной функции по параметру.

ТЕОРЕМА.  Пусть f(Z) является аналитической функцией в области G и непрерывной в области G (G включая граничные точки ), тогда во внутренних точках области G существует производная любого порядка от функции f(Z) причем для ее вычисления имеет место формула :

 (3)

С помощью формулы (3) можно получить производную любого порядка от аналитической функции  f (Z) в любой точке Z области ее аналитичности. Для доказательства этой теоремы используется формула (2) и соответственные рассуждения, которые привели к ее выводу.

ТЕОРЕМА МОРЕРА. Пусть f(Z) непрерывна в односвязной области G и интеграл от этой функции по любому замкнутому контуру, целиком принадлежащему  G равен 0. Тогда функция f (Z) является аналитической функцией в области G. Эта теорема обобщается и на случай многосвязной области G.

Разложение функции комплексного переменного в ряды.

Если функция f(x, y) определена и непрерывна вместе с частными производными (до n-го порядка ), то существует разложение этой функции в ряд Тейлора :

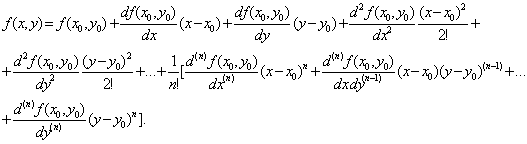
Итак, если задана функция f (z) комплексного переменного, причем f (z) непрерывная вместе с производными до n-го порядка, то:

               (2) – разложение в ряд Тейлора.

Формула (2) записана для всех Z принадлежащих некоторому кругу | Z-Z0 |

Функция f (z), которая может быть представлена в виде ряда (2) является аналитической функцией. Неаналитическая функция в ряд Тейлора не раскладывается.

                      (3)

        (4)

           (5)

Причем | Z | < R,  R ®  ¥ .>

Формулы ЭЙЛЕРА.

Применим разложение (3) положив, что Z = ix  и   Z= - ix;

                                                        (6)

Аналогично взяв Z = - ix  получим :

                                                      (7)

Из (6) и (7) можно выразить т.н. формулы Эйлера :

                 (8)

В общем случае :

    (9)

Известно, что :

      (10)

Тогда из (9) и (10) вытекает связь между тригонометрическими и гиперболическими косинусами и синусами:

Ряд ЛОРАНА.

Пусть функция f(z) является аналитической функцией в некотором круге радиусом R, тогда ее можно разложить в ряд Тейлора (2). Получим тот же ряд другим путем.

ТЕОРЕМА 1.

Однозначная функция  f(Z) аналитическая в круге радиусом  |Z-Z0| < R раскладывается в сходящийся к ней степенной ряд по степеням Z-Z>0.

Опишем в круге радиусом R окружность r, принадлежащую кругу с радиусом R.

Возьмем в круге радиуса r точку Z, а на границе области точку z , тогда  f(z) будет аналитична внутри круга с радиусом r и на его границе. Выполняется условие для существования интеграла Коши :

                                                                                        (13)

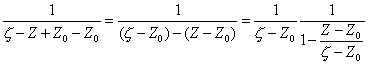                (11)

Поскольку

, то выражение  можно представить как сумму бесконечно убывающей геометрической прогрессии со знаменателем , т.е. :

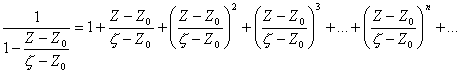
                     (12)

Представим равномерно сходящимся рядом в круге радиуса r, умножая (12) на 1/(2pi) и интегрируя по L при фиксированном  Z, получим : слева интеграл (13) который равен f (Z), а справа будет сумма интегралов :

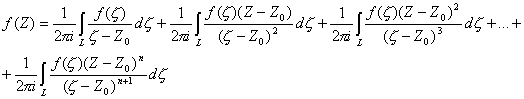
Обозначая , получим :             (14)

Это разложение функции f (Z) в круге R в ряд Тейлора. Сравнивая (14) с рядом (2) находим, что                                                                                  (15)

ТЕОРЕМА 2.

Если однозначная функция f(Z) аналитична вне круга с радиусом r с центром в точке Z0 для всех Z выполняется неравенство r < |Z-Z>0 |, то она представляется рядом :

                                                                        (16)

где  h - ориентированная против часовой стрелки окружность радиуса r (сколь угодно большое число). Если обозначить   (17) , получим :

                                                (18)

ТЕОРЕМА 3.

Если однозначная функция f(Z) аналитическая в кольце Z< |Z-Z>0 |0 существует M>0 и S0³0 такие, что выполняется условие : |f(t)|S0t

Рассмотрим функцию f(t)×e-pt , где р – комплексное число р = ( а + i b).

                                  (1)

Применим к этому соотношению формулу Эйлера :

Проинтегрировав это равенство получим :

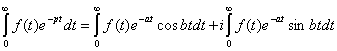                (2)

Оценим левую часть равенства (2) :

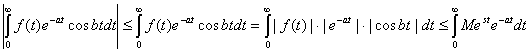
А согласно свойству (3)  |f(t)| < Me >S0t

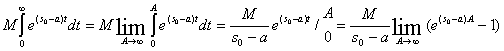
В случае если a>S0 имеем :

Аналогично можно доказать, что существует и сходится второй интеграл в равенстве (2).

Таким образом при a>S0 интеграл, стоящий в левой части равенства (2) также существует и сходится. Этот интеграл определяет собой функцию от комплексного параметра р :

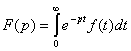             (3)

Функция F(p) называется изображением функции f(t) по Лапласу, а функция f(t) по отношению к F(p) называется оригиналом.

f(t) Ü F(p), где F(p) – изображение функции f(t) по Лапласу.

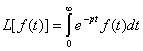 - это оператор Лапласа.

Смысл введения интегральных преобразований.

Этот смысл состоит в следующем : с помощью перехода в область изображения удается упростить решение многих задач, в частности свести задачу решения многих задач дифференциального, интегрального и интегро-дифференциального уравнения к решению алгебраических уравнений.

Теорема единственности: если две функции j( t)  и Y(t) имеют одно и то же изображение F(p), то эти функции тождественно равны.

Смысл теоремы : если при решении задачи мы определим изображение искомой функции, а затем по изображению нашли оригинал, то на основании теоремы единственности можно утверждать, что найденная функция является решением в области оригинала и причем единственным.

Изображение функций s0(t), sin (t), cos (t).

Определение:  называется единичной функцией.

Единичная функция удовлетворяет требованиям, которые должны быть наложены на функцию для существования изображения по Лапласу. Найдем это изображение :

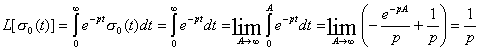
Изображение единичной функции

Рассуждая аналогичным образом получим изображение для функции sin(t) :

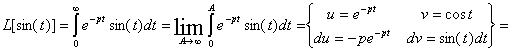
интегрируя по частям получим :

  т.е.

Аналогично можно доказать, что cos (t) переходит в функцию в области преобразований. Откуда :

Изображение функции с измененным масштабом независимого переменного.

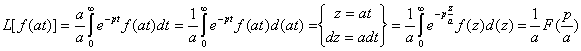где а – константа.

Таким образом :

  и

Свойства линейности изображения.

Теорема : изображение суммы нескольких функций умноженное на постоянные равны сумме изображений этих функций умноженных на те же постоянные.

Если , то , где

Теорема смещения : если функция F(p) это изображение f(t), то F(a+p) является изображением функции e-at f(t)                                 (4)

Доказательство :

Применим оператор Лапласа к левой части равенства (4)

Что и требовалось доказать.

Таблица основных изображений:

F(p)	f(t)	F(p)	f(p)
	1

Изображение производных.

Теорема. Если , то справедливо выражение :

                                             (1)

Доказательство :

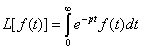
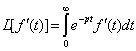
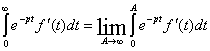                           (2)

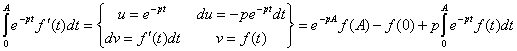    (3)

Подставляя (3) в (2) и учитывая третье условие существования функции Лапласа имеем :

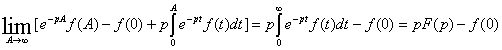
Что и требовалось доказать.

Пример: Решить дифференциальное уравнение :

  Если x(0)=0   и x’(0)=0

Предположим, что x(t) – решение в области оригиналов и , где - решение в области изображений.

Изображающее уравнение :

Теорема о интегрировании оригинала. Пусть  находится в области оригиналов, , тогда также оригинал, а его изображение .

Таким образом операции интегрирования в области оригиналов соответствует операция деления в области изображений.

Теорема о интегрировании изображений : Пусть  – функция оригинал, которая имеет изображение и  также оригинал, а - является сходящимся интегралом, тогда .

Толкование теоремы : операция деления на аргумент в области оригиналов соответствует операции интегрирования в пределах от р до ¥ в области изображений.

Понятие о свертке функций. Теорема о свертке.

Пусть заданы две функции a(t) и b(t), удовлетворяющие условиям существования изображения по Лапласу, тогда сверткой таких функций называется следующая функция :

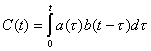            (1)

Свертка обозначается следующим образом :

                         (1’)

Равенства (1) и (1’) идентичны.

Свертка функции подчиняется переместительному закону.

Доказательство:

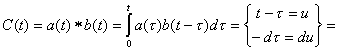
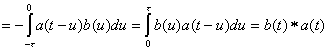
 Теорема о умножении изображений. Пусть и , тогда произведение изображений  представляется сверткой оригиналов .

Доказательство :

Пусть изображение свертки

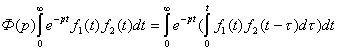                      (1)

Интеграл (1) представляет собой повторный интеграл относительно переменных t и t . Изменим порядок интегрирования. Переменные t и t входят в выражение симметрично. Замена переменной производится эквивалентно.

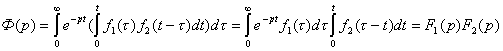
Если в последнем интеграле сделать замену переменной, то после преобразований последний интеграл преобразуется в функцию F2(p).

Операция умножения двух функций в пространстве изображений соответствует операции свертки их оригиналов в области оригиналов. Обобщением теоремы о свертке есть теорема Эфроса.

Теорема Эфроса. Пусть функция  находится в области оригиналов, , а Ф(р) и q(р) – аналитические функции в области изображений, такие, что , тогда  .

В практических вычислениях важную роль играет следствие из теоремы о свертке, наз. интеграл  Дюамеля. Пусть все условия теоремы выполняются, тогда

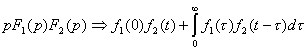  (2)

Соотношение (2) применяется при решении дифференциальных уравнений.

Обратное преобразование Лапласа.

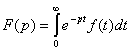 - Это прямое преобразование Лапласа.

Обратное преобразование есть возможность получить функцию-оригинал через известную функцию-изображение :

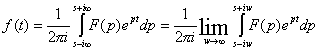, где s – некоторая константа.

Пользоваться формулой для обратного преобразования можно при определенном виде функции F(p), либо для численного нахождения функции-оригинала по известному изображению.

Теоремы разложения.

Известная методика разложения дробно-рациональных функций на сумму элементарных дробей (1)-(4) может быть представлена в виде двух теорем разложения.

Первая теорема разложения. Пусть F(p) – изображение некоторой функции, тогда эта функция представляется в виде ,  k – постоянная, может быть сколь угодно большим числом, , то возможен почленный переход в пространство оригиналов с помощью формулы : .

Вторая теорема разложения. Если изображение представляется дробно-рациональной функцией . Степень числа s меньше степени знаменателя n, знаменатель имеет корни a1, a2, …, a n соответствующий кратности k1, k2, …, kn , при этом k1+ k2 +…+ kn = n. В этом случае оригинал функции определяется по формуле :

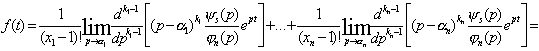
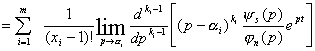                                       (3)

Например :

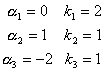
Связь между преобразованиями Фурье и Лапласа.

Преобразование Лапласа имеет вид :

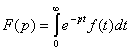                            (1)

На  f(t) наложены условия :

1) f(t) определена и непрерывна на всем интервале: (-¥ ; ¥ )

2) f(t) º 0 , t Î (- ¥ ;0)

3) При  M, S0 >0 , для всех t > 0 выполняется условие |f(t)|S0t

Если отказаться от условий 2 и 3, и считать, что f(t) принимает произвольное значение при t < 0, то вместо (1) можно рассмотреть следующий интеграл :>

                            (2)

Формула (2) – двустороннее преобразование Лапласа.

Пусть в (1) и (2)  p =a + in, где a и n – действительные числа.

Предположим, что Re(p) = a = 0, т.е.

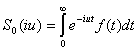                           (4)

                           (5)

(4) и (5) соответственно односторонние и двусторонние преобразования Фурье.

Для существования преобразования Фурье, функция должна удовлетворять условиям :

1) Должна быть определена на промежутке (-¥ ; ¥ ) , непрерывна всюду, за исключением конечного числа точек разрыва первого рода.

2) Любой конечный промежуток оси t можно разделить на конечное число промежутков, в каждом из которых функция либо кусочно-гладкая, либо кусочно-монотонная.

3) Функция абсолютно интегрируема : , это условие выполняется, если |f(t)|S0t

Из существования преобразования Лапласа не следует преобразование Фурье. Преобразования Фурье существуют для более узкого класса функций. Преобразования Фурье не существуют для постоянной и ограниченной функции : f(t) = C

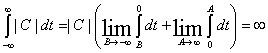
Аналогично преобразования Фурье не существуют и для гармоничных функций :

   т.к.

Если  f(t) = 0 при t>0 и преобразование для этой функции существует, то оно может быть получено из таблицы оригиналов и изображений для преобразования Лапласа путем замены параметра t на iu, но при этом необходимо убедиться, что F(p) не обращается в число справа от мнимой оси.

Если  f(t) ¹ 0, t

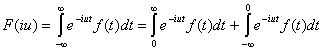     (6)

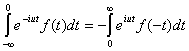
Обозначим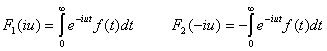

Очевидно, что                            (6’)

Функция (6) называется спектральной плотностью

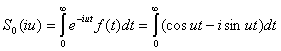
В связи с изложенным можно указать два пути отыскания спектральной плотности :

1) Вычисление интеграла (5)

2) Использование преобразования Лапласа или Фурье.

Непосредственное вычисление спектральной плотности для абсолютно интегрируемой функции.

Функция F(iu) может быть представлена, как комплексная функция действительной переменной

                                                (7)

|F(iu)| - амплитудное значение спектральной плотности, y (u) – фазовый угол.

В алгебраической форме : F(iu) = a(u) +ib(u)

                                           (8)

                                                      (9)

Для непосредственного вычисления спектральной плотности вычисляется интеграл (6), а затем по формулам (8) и (9) определяется амплитудное значение |F(iu)|  и фазовый угол y (u).

Пример.

Найти спектральную плотность импульса :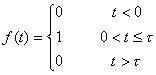

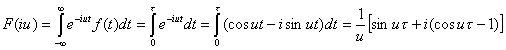
откуда , далее

Отыскание спектральной плотности для неабсолютно интегрируемых функций.

Прямое преобразование Фурье для таких функций не существует, существует преобразование Лагранжа.

Прямое преобразование Фурье необходимо :

1) Для облегчения процесса решения дифференциальных и интегральных уравнений.

2) Для исследования амплитудной и частотной характеристик спектральной плотности, определенной всюду на числовой оси.

Введем следующее определение спектральной плотности для неабсолютно интегрируемых функций:

Если для заданной функции y=f(t) существует непрерывное изображение по Лапласу F(p), то спектральной плотностью функции называется изображение функции по Лапласу при p = iu.

Спектральной плотностью  F1(iu) неабсолютно интегрируемой функции называется предел от спектральной плотности F2(iua) абсолютно интегрируемой функции.