Рефераты по рекламе
Рефераты по философии
Рефераты по финансам
Рефераты по химии
Рефераты по цифровым устройствам
Рефераты по экологическому праву
Рефераты по экономико-математическому моделированию
Рефераты по экономической географии
Рефераты по экономической теории
Рефераты по этике
Рефераты по юриспруденции
Рефераты по языковедению
Рефераты по юридическим наукам
Рефераты по истории
Рефераты по компьютерным наукам
Рефераты по медицинским наукам
Рефераты по финансовым наукам
Рефераты по управленческим наукам
Рефераты по строительным наукам
Психология педагогика
Промышленность производство
Биология и химия
Языкознание филология
Издательское дело и полиграфия
Рефераты по краеведению и этнографии
Рефераты по религии и мифологии
Рефераты по медицине
Рефераты по сексологии
Рефераты по москвоведению
Рефераты по экологии
Краткое содержание произведений
Рефераты по физкультуре и спорту
Топики по английскому языку
Рефераты по математике
Рефераты по музыке
Остальные рефераты
Курсовая работа: Спеціальні класи та функціональна повнота системи функцій алгебри логіки. Теорема Поста
Курсовая работа: Спеціальні класи та функціональна повнота системи функцій алгебри логіки. Теорема Поста
Міністерство освіти і науки України
Національний університет «Львівська політехніка»
Кафедра Прикладної математики
Курсова робота
з курсу «Дискретна математика»
на тему
«Функціональна повнота системи функцій алгебри логіки. Спеціальні класи функцій алгебри логіки. Теорема Поста»
Виконала: ст. гр.ІФ-31
Мартинюк Н.О
Прийняла: Тесак І.Є
Львів – 2011р.
В роботі розглянуто поняття функціональної повноти системи функцій алгебри логіки, спеціальних класів функцій алгебри логіки, а також досліджено умови виконання теорема Поста.
В середовищі програмування С# реалізується алгоритм, який визначає чи є система функцій алгебри логіки функціонально повна, вид повноти.
Засади алгебри логіки були сформульовані британцем Джорджем Булем у 1847 році. Пізніше її розвивали Чарлз Пірс, Генрі Шеффер, П. С. Порецький, Бертран Рассел, Давид Гільберт та ін.
Відтоді ця система застосовується для вирішення широкого спектру проблем математичної логіки та теорії множин, та особливо конструювання цифрової електроніки (початок використання алгебри логіки для синтезу перемикальних (релейних) схем був покладений в 1938 році роботами відомого американського вченого Клода Шеннона).
Алгебра логіки (Булева логіка, двійкова логіка, двійкова алгебра) — розділ математичної логіки, що вивчає систему логічних операцій над висловлюваннями. Тобто, представлення логіки у вигляді алгебраїчної структури.
Спочатку проблематика алгебри логіки перетиналась з проблематикою алгебри множин (теоретико-множинні операції).
Проте із закінченням формування теорії множин, що відбулось в 70-тих роках 19 століття, яка включила в себе алгебру множин, і подальшим розвитком математичної логіки, предмет алгебри логіки значно змінився.
Сучасна алгебра логіки розглядає операції над висловлюваннями, як булеву функцію і вивчає відносно них такі питання, як:
-таблиці істинності;
-функціональна повнота;
-замкнені класи;
-представлення у вигляді: ДНФ, КНФ, полінома Жегалкіна.
Базовими елементами алгебри логіки є висловлювання. Висловлювання будуються над множиною {B, , , , 0, 1}, де B — булева множина, над елементами якої визначені три операції:
- заперечення (унарна операція),
- кон'юнкція (бінарна),
- диз'юнкція (логічна, бінарна),
- константи — логічний нуль 0 та логічна одиниця 1.
Функціональна повнота системи функцій алгебри логіки відіграє важливу роль в математичній логіці.
Розділ 1. Функціональна повнота системи функцій алгебри логіки
1.1. Функції алгебри логіки
Визначення. Нехай
Е2={0,1} основна множина, тоді Е![]() ={
={![]() }. Тоді всюди визначеною булевою
функцією називаємо відображення
}. Тоді всюди визначеною булевою
функцією називаємо відображення ![]() . Таку функцію можна задати
таблично а також як суперпозицію інших, простіших функцій. Наприклад, для n=1:
. Таку функцію можна задати
таблично а також як суперпозицію інших, простіших функцій. Наприклад, для n=1:
Булева функція табличне зображення.
Таблиця №1
|
|
|
|
|
|
| 0 | 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 |
Функція 0
називається константою нулем, функція 1 – константою одиницею, функція х –
тотожною, а функція ![]() - запереченням х (
- запереченням х (![]() ).
).
Булевою функцією
називається функція ![]() в якій всі аргументи
в якій всі аргументи ![]() є незалежними,
і сама функція є логічними змінними, що приймають лише два значення 0 та 1. Ці
функції можуть бути задані аналітично, геометрично або за допомогою таблиць
істинності. Всі елементарні булеві функції двох змінних представлені таблицею
істинності.
є незалежними,
і сама функція є логічними змінними, що приймають лише два значення 0 та 1. Ці
функції можуть бути задані аналітично, геометрично або за допомогою таблиць
істинності. Всі елементарні булеві функції двох змінних представлені таблицею
істинності.
Таблиця істинності булевих функцій двох змінних.
Таблиця №2
| № |
X= 0 Y= 0 |
0 1 |
1 0 |
1 1 |
fк (X,Y) |
| 1 | 0 | 0 | 0 | 0 |
|
| 2 | 0 | 0 | 0 | 1 |
|
| 3 | 0 | 0 | 1 | 0 |
|
| 4 | 0 | 0 | 1 | 1 |
|
| 5 | 0 | 1 | 0 | 0 |
|
| 6 | 0 | 1 | 0 | 1 |
|
| 7 | 0 | 1 | 1 | 0 |
|
| 8 | 0 | 1 | 1 | 1 |
|
| 9 | 1 | 0 | 0 | 0 |
|
| 10 | 1 | 0 | 0 | 1 |
|
| 11 | 1 | 0 | 1 | 0 |
|
| 12 | 1 | 0 | 1 | 1 |
|
| 13 | 1 | 1 | 0 | 0 |
|
| 14 | 1 | 1 | 0 | 1 |
|
| 15 | 1 | 1 | 1 | 0 |
|
| 16 | 1 | 1 | 1 | 1 |
|
Більшість із шістнадцяти булевих функцій f(x, у) часто застосовуються на практиці. Оскільки дані функції використовуються як у математиці, так і в програмуванні, вони можуть мати різне позначення.
Позначення булевих функцій та їх назви.
Таблиця №3
| Функція | Позначення | Назва |
|
|
0 | константа 0 |
|
|
|
Кон'юнкція (логічне «і») — двомісна
логічна операція, що має значення «істина», якщо всі операнди мають значення
«істина». Операція відображає вживання сполучника «і» в логічних
висловлюваннях. |
|
|
|
заперечення імплікації |
|
|
|
Повторення першого аргументу |
|
|
|
заперечення оберненої імплікації |
|
|
У | Повторення другого аргументу |
|
|
х |
Виключна диз'юнкція (XOR, додавання за модулем два) — двомісна логічна операція, що приймає значення «істина» тоді і тільки тоді коли значення «істина» має рівно один з її операндів. Виключна диз'юнкція є запереченням логічної еквівалентності. |
|
|
|
Диз'юнкція (логічне «або») — двомісна логічна операція, що має значення «істина», якщо хоча б один з операндів має значення «істина». Операція відображає вживання сполучника «або» в логічних висловлюваннях. Позначається в програмуванні як or. |
|
|
|
Стрілка Пірса (операція NOR) — двомісна логічна операція, яка є запереченням диз'юнкції; тому значення «істина» одержується тільки тоді, коли обидва операнди мають значення «хиба». |
|
|
|
Еквівалентність — двомісна логічна операція, що має значення «істина», якщо обидва операнди мають однакове значення. Операція відображає вживання сполучника «тоді і тільки тоді» в логічних висловлюваннях. |
|
|
|
заперечення другого аргументу |
|
|
|
обернена імплікація |
|
|
|
заперечення першого аргументу |
|
|
|
Імплікація – двомісна логічна операція, що має значення «хиба», тоді і тільки тоді, коли перший операнд має значення «істина», а другий — «хиба». |
|
|
|
Штрих Шеффера (операція NAND) — двомісна логічна операція, яка є запереченням кон'юнкції; тому значення «хиба» одержується тільки тоді, коли обидва операнди мають значення «істина». |
|
|
1 | константа 1 |
1.2 Функціональна повнота
Визначення. Множина функцій алгебри логіки А називається повною системою (в Р2), якщо будь-яку функцію алгебри логіки можна виразити формулою над А.
Теорема 1[1,
ст.6]. Система А={![]() } є повною.
} є повною.
Доведення. Якщо
функція алгебри логіки ![]() відмінна від тотожного нуля, то f
виражається у вигляді досконалої диз’юнктної нормальної форми, в яку входять
лише диз’юнкція, кон’юнкція та заперечення. Якщо ж
відмінна від тотожного нуля, то f
виражається у вигляді досконалої диз’юнктної нормальної форми, в яку входять
лише диз’юнкція, кон’юнкція та заперечення. Якщо ж ![]() , то
, то ![]() . Теорема доведена.
. Теорема доведена.
Лема 1[1, ст.6]. Якщо система А – повна, і будь-яка функція може бути виражена формулою над іншою системою В, то В – теж повна система.
Доведення.
Розглянемо довільну функцію алгебри логіки ![]() і дві системи функцій А={g1,
g2,…} і B={h1, h2,…}. Оскільки система А
повна, функція
і дві системи функцій А={g1,
g2,…} і B={h1, h2,…}. Оскільки система А
повна, функція ![]() може бути виражена у вигляді
формули над нею
може бути виражена у вигляді
формули над нею ![]() , де
, де ![]() , тобто функція
, тобто функція ![]() представляється у вигляді
представляється у вигляді ![]() , що означає що вона може бути
представлена формулою над В. Перебираючи таким чином всі функції алгебри
логіки, отримаємо, що система В також повна. Лема доведена.
, що означає що вона може бути
представлена формулою над В. Перебираючи таким чином всі функції алгебри
логіки, отримаємо, що система В також повна. Лема доведена.
Теорема 2[1, ст.6]. Такі системи є повними в Р2
1.
![]() ;
;
2.
![]() ;
;
3.
![]() ;
;
4.
![]()
![]()
Доведення.
1.
Відомо
(теорема 1), що система А=![]() повна. Покажемо, що система В=
повна. Покажемо, що система В=![]() повна. З
закону де Моргана
повна. З
закону де Моргана ![]() отримуємо, що
отримуємо, що ![]() , тобто кон’юнкція
виражається через диз’юнкцію і заперечення, і всі функції системи А виражаються
формулами над системою В. Система В повна (лема 1).
, тобто кон’юнкція
виражається через диз’юнкцію і заперечення, і всі функції системи А виражаються
формулами над системою В. Система В повна (лема 1).
2.
Аналогічно
пункту 1: ![]() =
=![]() із леми 1
випливає, що вираз пункту 2 є правильний.
із леми 1
випливає, що вираз пункту 2 є правильний.
3.
![]() згідно леми 1
система повна.
згідно леми 1
система повна.
4.
![]() згідно леми 1
система повна.
згідно леми 1
система повна.
Розділ 2. Спеціальні класи функцій алгебри логіки
2.1 Замкнені класи
Визначення. Нехай
А![]() Р. Тоді
замиканням А називається множина всіх функцій алгебри логіки, які можна
виразити формулами над А.
Р. Тоді
замиканням А називається множина всіх функцій алгебри логіки, які можна
виразити формулами над А.
Позначення :![]() .
.
Мають місце наступні властивості
1.
![]() ;
;
2.
![]() ;
;
3.
![]() .
.
Визначення.
Система функцій алгебри логіки А називається повною, якщо ![]() .
.
Визначення. Нехай
А![]() Р. Тоді
система А називається замкнутим класом, якщо замикання А збігається з
Р. Тоді
система А називається замкнутим класом, якщо замикання А збігається з ![]() .
.
Теорема 3[1, ст.8]. Нехай А замкнений клас, А![]() Р2 і В
Р2 і В![]() А. Тоді В – неповна
система (підмножина неповної системи буде також неповна система).
А. Тоді В – неповна
система (підмножина неповної системи буде також неповна система).
Доведення
![]()
отже В – неповна система.
Теорема доведена
Приклади замкнених класів
Клас ![]()
Класу ![]() належать такі
функції:
належать такі
функції: ![]()
Класу ![]() не належать такі функції:
не належать такі функції: ![]()
Теорема 4[1, ст.8]. Клас ![]() – замкнений .
– замкнений .
Доведення
Нехай ![]()
Розглянемо функцію
![]()
Серед змінних
функцій ![]() можуть
зустрітись однакові, тому в якості змінних функції
можуть
зустрітись однакові, тому в якості змінних функції ![]() візьмемо всі різні із них.
візьмемо всі різні із них.
Тоді ![]() , отже функція
, отже функція
![]() також
зберігає 0. Розглянутий тільки окремий випадок (без змінних в якості
аргументів). Проте, оскільки тотожна функція зберігає нуль, підстановка простих
змінних еквівалентна підстановці тотожної функції, теорема доведена.
також
зберігає 0. Розглянутий тільки окремий випадок (без змінних в якості
аргументів). Проте, оскільки тотожна функція зберігає нуль, підстановка простих
змінних еквівалентна підстановці тотожної функції, теорема доведена.
Клас ![]()
Класу ![]() належать такі
функції:
належать такі
функції: ![]()
Класу ![]() не належать такі
функції:
не належать такі
функції: ![]()
Теорема 5[1, ст.8]. Клас ![]() – замкнений.
– замкнений.
Доведення
Нехай
![]()
Розглянемо функцію
![]()
Серед змінних
функцій ![]() можуть
зустрітись однакові, тому в якості змінних функції
можуть
зустрітись однакові, тому в якості змінних функції ![]() візьмемо всі різні із них.
візьмемо всі різні із них.
Тоді ![]() , отже функція
, отже функція
![]() також
зберігає 1. Розглянутий тільки окремий випадок (без змінних в якості
аргументів). Проте, оскільки тотожна функція зберігає одиницю, підстановка простих
змінних еквівалентна підстановці тотожної функції, теорема доведена.
також
зберігає 1. Розглянутий тільки окремий випадок (без змінних в якості
аргументів). Проте, оскільки тотожна функція зберігає одиницю, підстановка простих
змінних еквівалентна підстановці тотожної функції, теорема доведена.
Клас ![]() лінійних
функцій.
лінійних
функцій.
Визначення.
Функція алгебри логіки ![]() називається лінійною, якщо
називається лінійною, якщо
![]()
де ![]()
Іншими словами, в поліномі лінійної функції немає доданків, що містять кон'юнкцію.
Класу ![]() належать такі
функції:
належать такі
функції: ![]()
Класу ![]() не належать
такі функції:
не належать
такі функції: ![]()
Теорема 6. Клас ![]() – замкнений.
– замкнений.
Доведення. Оскільки
тотожна функція - лінійна, досить розглянути тільки випадок підстановки у формули
функцій : нехай ![]() Достатньо показати, що
Достатньо показати, що ![]() . Дійсно, якщо
не враховувати доданків
. Дійсно, якщо
не враховувати доданків ![]() , то всяку лінійну функцію можна зобразити
у вигляді
, то всяку лінійну функцію можна зобразити
у вигляді ![]() .
Якщо тепер замість кожного
.
Якщо тепер замість кожного ![]() підставити лінійний вираз, то
вийде знову лінійний вираз, константа 0 або константа 1.
підставити лінійний вираз, то
вийде знову лінійний вираз, константа 0 або константа 1.
2.2 Клас самодвоїстих функцій та його замкненість
Визначення.
Функцією двоїстою до функції алгебри логіки ![]() називається функція
називається функція ![]()
Теорема 7. Принцип двоїстості
Нехай
![]()
Тоді ![]()
Доведення.
Розглянемо

Теорема доведена.
Клас ![]() самодвоїстих функцій.
самодвоїстих функцій.
Визначення. Функція алгебри логіки ![]() називається
самодвоїстою, якщо
називається
самодвоїстою, якщо ![]() Тобто
Тобто ![]() .
.
Класу ![]() належать функції
належать функції
![]()
Класу ![]() не належать
функції
не належать
функції
![]()
Теорема 8. Клас ![]() – замкнений.
– замкнений.
Доведення. Нехай
![]()
![]()
Тоді з принципу двоїстості випливає, що
![]()
Отже, ![]()
Теорема доведена
2.3 Клас монотонних функцій та його замкненість
Визначення
Нехай ![]()
Тоді ![]()
Визначення.
Функція алгебри логіки ![]() називається монотонною, якщо для
двох будь-яких порівняльних наборів
називається монотонною, якщо для
двох будь-яких порівняльних наборів ![]() і
і ![]() виконується імплікація
виконується імплікація
![]()
Клас ![]() усіх
монотонних функцій.
усіх
монотонних функцій.
Класу ![]() належать такі
функції:
належать такі
функції: ![]()
Класу ![]() не належать
такі функції:
не належать
такі функції: ![]()
Теорема 9. Клас ![]() - замкнений
- замкнений
Доведення. Оскільки тотожна функція монотонна, достатньо перевірити лише випадок суперпозиції функцій.
Нехай ![]() , для
будь-якого
, для
будь-якого ![]() і
і
![]()
Розглянемо
довільні набори ![]() , такі, що
, такі, що ![]() . Позначимо
. Позначимо ![]() Тоді для
будь-якого
Тоді для
будь-якого ![]() маємо
маємо
![]() , тобто
, тобто ![]() . Позначимо
. Позначимо ![]() .
.
Тоді за
визначенням ![]() і
в силу монотонності функції
і
в силу монотонності функції ![]() . Але
. Але ![]() і нерівність
і нерівність ![]() , отже
, отже ![]() .
.
Теорема доведена
Критерій Поста формулює необхідну і достатню умову повноти для системи функцій: система булевих функцій є повна тоді і тільки тоді, коли вона не міститься повністю в жодному з класів Т0, Т1, S, M, L.
Повна система називається базисом, якщо вона перестає бути повною при вилученні з неї довільної функції.
Прикладом повних систем із однією функцією є штрих Шеффера та стрілка Пірса.
Широко відомими є такі повні системи булевих функцій:
1.
Булева
алгебра — алгебраїчна структура з двома бінарними та унарною операціями (![]() ), відповідно
до законів де Моргана вона не є базисом оскільки диз’юнкцію чи кон’юнкцію можна
виключити.
), відповідно
до законів де Моргана вона не є базисом оскільки диз’юнкцію чи кон’юнкцію можна
виключити.
2.
Алгебра
Жегалкіна (![]()
![]() ,
, ![]()
![]() 1 – константа одиниця) – є базисом.
1 – константа одиниця) – є базисом.
Перша система використовується для представлення булевих функцій у вигляді диз’юнктних та кон’юнктних нормальних форм, друга – для представлення у вигляді поліномів Жегалкіна.
Приклад. Система
функцій {![]() }
є функціонально повною, але система функцій {
}
є функціонально повною, але система функцій {![]() } не є функціонально повна.
} не є функціонально повна.
Якщо у функціонально повній системі є функції константи «0» чи константи «1», то вона послаблено функціонально повна.
Приклад. Система
функцій {![]() },
що поповнена константою одиниці , тобто {{
},
що поповнена константою одиниці , тобто {{![]() },1}, є послаблено функціонально
повна.
},1}, є послаблено функціонально
повна.
Максимальна кількість булевих функцій у базисі – 4.
Деколи кажуть про
систему функцій повну в деякому класі, а також про базис цього класу. Наприкад,
систему {![]() }
можна назвати базисом класу лінійних функцій.
}
можна назвати базисом класу лінійних функцій.
Визначення. Система булевих функцій називається мінімально повним базисом, якщо видалення з неї будь-якої функції перетворює цю систему в неповну.
Приклад. Мінімально
повний базис є {![]() }, але система {
}, але система {![]() } не є мінімально повним
базисом.
} не є мінімально повним
базисом.
Функціонально Замкнуті класи, відмінні від порожнього класу і сукупності всіх можливих булевих функцій, називаються власними функціонально замкненими класами.
Отже, довільна функція, яку можна зобразити формулою з використанням функцій множини P, також входить в цю множину
1.
![]() - замкнутість
щодо заміни змінних;
- замкнутість
щодо заміни змінних;
2.
![]() - замкнутість
щодо суперпозиції.
- замкнутість
щодо суперпозиції.
В 1941 році Еміль Пост надав повний опис замкнених класів, який назвали решіткою Поста.
Особливо важливими замкнутими класами є так звані передповні класи.
алгебра логіка функція теорема поста
2.4 Передповні класи
Визначення. Нехай
![]() .
. ![]() називається передповним
класом, якщо
називається передповним
класом, якщо
1.
![]() ;
;
2.
![]() .
.
Теорема 10. В ![]() передповними є
лише такі 5 класів:
передповними є
лише такі 5 класів: ![]()
Доведення
1. Покажемо спочатку, що жоден з цих п’яти класів не міститься в іншому. Для цього достатньо для кожного з цих п’яти класів вказати чотири функції, що належать цьому класу, але що не належать іншим чотирьом
|
|
|
|
|
|
|
|
|
0 |
|
|
0 | |
|
|
1 |
|
|
1 | |
|
|
1 | 0 |
|
0 | |
|
|
1 | 0 |
|
0 | |
|
|
|
|
|
|
2.
Доведемо,
що всі класи – T0, T1, L, S, M є передповними. Дійсно, нехай ![]() і
і ![]() . Тоді системи
. Тоді системи ![]() немає в жодному із
класів Поста. Отже, система
немає в жодному із
класів Поста. Отже, система ![]() – повна і
– повна і ![]() – передповний клас.
– передповний клас.
3.
Нехай ![]() - передповний
клас
- передповний
клас
Тоді ![]()
Якщо ![]() , то
, то ![]()
Жоден з передповних класів не міститься повністю в об'єднанні чотирьох інших класів; довільний замкнутий клас, відмінний від P2, повністю міститься хоча б в одному з п'яти передповних класів.
Таблиця №3
| Хиба | Істина | Заперечення | Кон'юнкція, AND | Диз'юнкція, OR | Виключна диз'юнкція XOR | Еквівалентність, XNOR | Імплікація | Заперечення імплікації | Штрих Шеффера, NAND | Стрілка Пірса, NOR | |
| Т0 | • | • | • | • | • | ||||||
| Т1 | • | • | • | • | • | ||||||
| S | • | ||||||||||
| M | • | • | • | • | |||||||
| L | • | • | • | • | • |
Щоб вибрати функціонально повну систему функцій потрібно, щоб таблиця з їхніх стовпців в кожному рядку містила хоча б одну порожню клітинку.
Щоб вибрати базис для класу потрібно, щоб таблиця з їхніх стовпців в кожному рядку (крім рядка цього класу) містила хоча б одну порожню клітинку.
2.5 Інші важливі замкнені класи
1.
Клас
кон'юнкцій K, що є замиканням множини операцій {![]() }. Він представляє собою множину
функцій виду
}. Він представляє собою множину
функцій виду ![]() .
.
2.
Клас
диз'юнкцій D, що є замиканням множини операцій {![]() }. Він представляє собою множину
функцій виду
}. Він представляє собою множину
функцій виду ![]() .
.
3. Клас U функцій одної змінної, що містить тільки константи, заперечення та селектор (функцію, що тотожна одній зі своїх змінних).
4.
Клас ![]() функцій (m -
натуральне число, більше одиниці), в яких для довільних m наборів, на яких
функція рівна нулю, знайдеться змінна, яка теж рівна нулю на всіх цих наборах.
функцій (m -
натуральне число, більше одиниці), в яких для довільних m наборів, на яких
функція рівна нулю, знайдеться змінна, яка теж рівна нулю на всіх цих наборах.
5.
Клас ![]() функцій, для
яких виконується умова
функцій, для
яких виконується умова ![]() .
.
6.
Клас ![]() функцій (m -
натуральне число, більше одиниці), в яких для довільних m наборів, на яких
функція рівна 1, знайдеться змінна, яка теж рівна 1 на всіх цих наборах.
функцій (m -
натуральне число, більше одиниці), в яких для довільних m наборів, на яких
функція рівна 1, знайдеться змінна, яка теж рівна 1 на всіх цих наборах.
7.
Клас ![]() функцій, для
яких виконується умова
функцій, для
яких виконується умова ![]() .
.
В 1941 році Еміль Пост показав, що довільний замкнутий клас є перетином скінченної кількості вищеописаних класів. Також Пост встановив, що довільний замкнутий клас може бути породжений скінченним базисом.
Властивості:
1. Перетин замкнутих класів є замкнутим класом.
2. Об'єднання замкнутих класів може не бути замкнутим класом.
3. Доповнення замкнутого класа булевих функцій до множини всіх булевих функцій P2 не є замкнутим класом.
Лема 2(про
несамодвоїсту функцію.) [1, ст. 10]. З будь-якої несамодвоїстої функції алгебри
логіки ![]() ,
підставляючи замість усіх змінних функції
,
підставляючи замість усіх змінних функції ![]() і
і![]() , можна отримати
, можна отримати![]() .
.
Доведення
Нехай![]()
Тоді ![]()
![]()
Побудуємо функцію
![]() так:
так:
![]()
Дійсно
![]()
і![]()
Зауважимо, що підстановка задовольняє умові теореми, так
як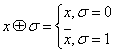
Лемy доведенo.
Лема 3(про
немонотонну функцію.) [1, ст. 11]. З будь-якої немонотонної функції алгебри
логіки ![]() ,
підставляючи замість усіх змінних функції
,
підставляючи замість усіх змінних функції ![]() , можна отримати функцію
, можна отримати функцію
![]()
Доведення
Нехай ![]() . Тоді існують
такі набори
. Тоді існують
такі набори ![]() і
і![]() , що
, що ![]() (тобто
(тобто ![]() і
і ![]() ) і
) і ![]() . Виділимо ті
розряди
. Виділимо ті
розряди ![]() наборів
наборів ![]() , в яких вони відрізняються.
Очевидно, в наборі
, в яких вони відрізняються.
Очевидно, в наборі ![]() ці розряди
ці розряди
рівні 0, а в
наборі ![]() . Розглянемо послідовність наборів
. Розглянемо послідовність наборів
![]() таких,
що
таких,
що![]() , де
, де ![]() виходить з
виходить з ![]() заміною одного
з нулів, розташованого в одній з позицій
заміною одного
з нулів, розташованого в одній з позицій ![]() , на одиницю (при цьому набори
, на одиницю (при цьому набори ![]() і
і ![]() - сусідні).
- сусідні).
Оскільки ![]() , а
, а ![]() , серед наборів
, серед наборів ![]() знайдуться два сусідні
знайдуться два сусідні ![]() і
і ![]() , такі що
, такі що ![]() і
і ![]() . Нехай вони відрізняються в r-му
розряді:
. Нехай вони відрізняються в r-му
розряді: ![]() ,
,![]() . Тоді
визначимо функцію
. Тоді
визначимо функцію ![]() так:
так: ![]() . Справді, тоді
. Справді, тоді ![]() ,
, ![]() і
і ![]() . Лема доведена.
. Лема доведена.
Лема 4(про
нелінійну функцію.) [1, ст. 11]. З будь-якої нелінійної функції алгебри логіки ![]() , підставляючи
замість усіх змінних
, підставляючи
замість усіх змінних![]() , можна отримати
, можна отримати ![]() або
або ![]() .
.
Доведення. Нехай ![]() . Розглянемо поліном Жегалкіна
цієї функції.
. Розглянемо поліном Жегалкіна
цієї функції.
З її нелінійності
випливає, що в ньому присутні складові виду![]() . Будемо вважати, що існує добуток
. Будемо вважати, що існує добуток
![]() . Таким
чином, поліном Жегалкіна цієї функції виглядає так
. Таким
чином, поліном Жегалкіна цієї функції виглядає так
![]() ,
,
Причому ![]()
Інакше кажучи, ![]() такі, що
такі, що![]() .
.
Розглянемо допоміжну функцію
![]() .
.
Тоді функція
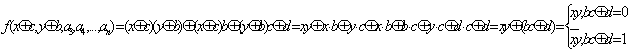
Лему доведено.
Теорема 11
Cистема функцій алгебри логіки
![]() є повною
в
є повною
в ![]() тоді і
тільки тоді, коли вона не міститься цілком в жодному із класів:
тоді і
тільки тоді, коли вона не міститься цілком в жодному із класів: ![]() .
.
Доведення
Необхідність.
Нехай ![]() –
повна система,
–
повна система, ![]() – будь-який з класів
– будь-який з класів ![]() і нехай
і нехай ![]()
Тоді
![]()
Отримане протиріччя завершує обґрунтування необхідності.
Достатність. Нехай
![]()
Тоді в ![]() існують
функції
існують
функції
![]()
Достатньо показати, що
![]()
Розіб’ємо доведення на три частини: отримання заперечення, констант і кон’юнкції.
1.
Отримання
![]() .
Розглянемо функцію
.
Розглянемо функцію ![]() і введемо функцію
і введемо функцію ![]() . Так як функція
. Так як функція ![]() не зберігає 0,
не зберігає 0,
![]() . Можливі
два випадки:
. Можливі
два випадки: ![]() або
або ![]() . Розглянемо функцію
. Розглянемо функцію ![]() і аналогічним
способом введемо функцію
і аналогічним
способом введемо функцію ![]() . Так як функція
. Так як функція ![]() не зберігає одиницю,
не зберігає одиницю, ![]() . Можливі
також два випадки:
. Можливі
також два випадки: ![]() або
або ![]() . Якщо хоч в одному випадку
отримали шукане значення, то пункт завершений. Якщо ж в обидвох випадках
отримали константи, то згідно з лемою 3(про немонотонну функцію), підставляючи
функцію
. Якщо хоч в одному випадку
отримали шукане значення, то пункт завершений. Якщо ж в обидвох випадках
отримали константи, то згідно з лемою 3(про немонотонну функцію), підставляючи
функцію ![]() замість
усіх змінних константи і тотожні функції, можна отримати заперечення. Отже,
заперечення отримане.
замість
усіх змінних константи і тотожні функції, можна отримати заперечення. Отже,
заперечення отримане.
2.
Отримання
константи 0 та 1. Маємо ![]() . Згідно з лемою 2(про
несамодвоїсту функцію), підставляючи замість усіх змінних функції
. Згідно з лемою 2(про
несамодвоїсту функцію), підставляючи замість усіх змінних функції ![]() заперечення(отримане
в попередньому пункті) і тотожну функцію, можна отримати константи
заперечення(отримане
в попередньому пункті) і тотожну функцію, можна отримати константи
![]()
Константи отримані.
3.
Отримання
кон’юнкції ![]() .
Маємо функцію
.
Маємо функцію ![]() . Згідно з лемою4(про нелінійну
функцію), підставляючи у функцію
. Згідно з лемою4(про нелінійну
функцію), підставляючи у функцію ![]() замість усіх змінних константи і
заперечення(які були отримані у попередніх пунктах доведення), можна отримати
кон’юнкцію або заперечення кон’юнкції. Проте на першому етапі заперечення вже
отримано, отже, завжди можна отримати кон’юнкцію
замість усіх змінних константи і
заперечення(які були отримані у попередніх пунктах доведення), можна отримати
кон’юнкцію або заперечення кон’юнкції. Проте на першому етапі заперечення вже
отримано, отже, завжди можна отримати кон’юнкцію
![]()
Кон’юнкція отримана.
Отже, ![]()
Остання рівність випливає з другого пункту теореми 2. Враховуючи лему 1 достатність доведена.
Розділ 4. Постановка і реалізація задачі
Постановка задачі.
Задано систему функцій алгебри логіки. Визначити чи є ця система функціонально повна, визначити вид повноти.
Реалізація задачі.
Для розв’язання задачі написана програма, яка реалізована в середовищі С#. Вона є об’єктно орієнтована.
Алгоритм реалізації програми.
Вводжу систему функцій алгебри логіки. За теоремою Поста перевіряю її на повноту(послаблену повноту), використовуючи таблицю №3.
Для коректної роботи програми достатньо таких характеристик комп’ютера: Windows ХР 2008, процесор з тактовою частотою – 200 МГц, оперативна пам'ять – 32 Мб, вільна пам'ять на жорсткому диску – 200 Мб.
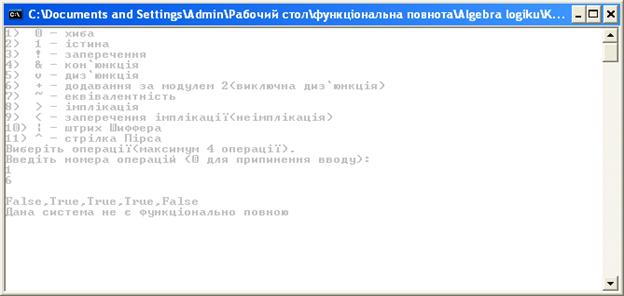
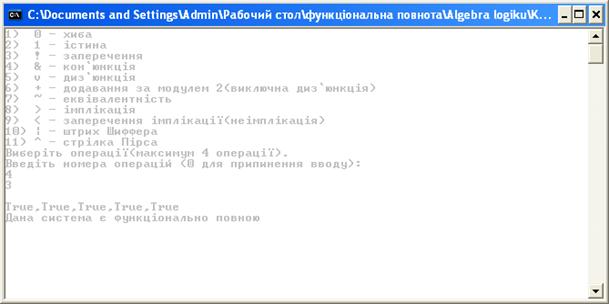
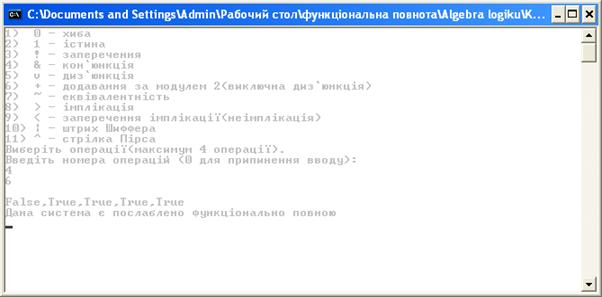
Необхідно коректно вводити вхідні дані. Для цього користувачеві надається інструкція з позначенням всіх операцій:
1 – хиба;
2 – істина;
3 – заперечення;
4 – кон’юнкція;
5 – диз’юнкція:
6 – додавання за модулем 2;
7 – еквівалентність;
8 – імплікація;
9 – заперечення імплікації;
10 – штрих “Шеффера”;
11 – стрілка Пірса.
При некоректному вводі вхідних даних користувачеві буде виведене повідомлення про помилку.
Кожну наступну вибрану операцію потрібно вводити після натискання кнопки Enter. Для завершення вводу потрібно двічі натиснути кнопку Enter.
Контрольні приклади виконання програми
Засади алгебри логіки були сформульовані британцем Дж. Булем в 1847 році. Зараз алгебра логіки широко використовується для конструювання цифрової електроніки, синтезу перемикальних (релейних) схем.
Еміль Пост (11.02.1897 - 21.04.1954) – американський математик і логік, зробив великий внесок у розвиток досліджень щодо питання повноти системи функцій алгебри логіки. Ним був отриманий ряд фундаментальних результатів в математичній логіці, він дав одне з найбільш вживаних визначень понять несуперечності і повноти формальних систем числення, а також йому належить доведення функціональної повноти і дедуктивної повноти (у широкому і вузькому сенсі) висловлювань.
Також вивчаючи складні спеціальні канали диференціального аналізатора, американський науковець Клод Шеннон бачив, що Булеву алгебру і двійкову арифметику можна використовувати, щоб спростити розташування електромеханічних реле, які тоді використовувалися у телефонах. Використання цієї властивості електричних перемикачів є базовою логічною концепцією, яка лежить в основі всіх електронних цифрових комп'ютерів.
Питання функціональної повноти алгебри логіки відіграє важливу роль в математичній логіці: всі двомісні логічні операції числення висловлювань можуть бути виражені через кон'юнкцію і заперечення, або через диз'юнкцію і заперечення, або через імплікацію і заперечення, або навіть через єдину операцію антикон'юнкцію («штрих Шефера»), тобто всі ці сімейства логічних в'язок є функціонально повними класами операцій алгебри логіки.
Список використаної літератури
1. Алексеев В.Б., Поспелов А.Д. Дискретная математика. – М., 2002. – 44с.
2. Белоусов А.И., Ткачев С.Б. Дискретная математика. –М.,2004. – 743с .
3. Мартинюк О.М. Основи дискретної математики. – Одеса: Наука і техніка, 2008.-300с.
4. Борисенко О.А. Лекції з дискретної математики (множини і логіка): навчальний посібник. – 3-є вид., випр. і доп. – Суми: ВДТ «Університетська книга», 2002. – 180 с.
5. Плотников А.Д. Дискретная математика: учебное пособие. – М.: Новое знание, 2005. – 288 с.
6. Основи дискретної математики Капітонова Ю.В., Кривий С.Л., Летичевський О.А. та ін.– К.: Наукова думка, 2002. – 580 с.