
Рефераты по рекламе
Рефераты по философии
Рефераты по финансам
Рефераты по химии
Рефераты по цифровым устройствам
Рефераты по экологическому праву
Рефераты по экономико-математическому моделированию
Рефераты по экономической географии
Рефераты по экономической теории
Рефераты по этике
Рефераты по юриспруденции
Рефераты по языковедению
Рефераты по юридическим наукам
Рефераты по истории
Рефераты по компьютерным наукам
Рефераты по медицинским наукам
Рефераты по финансовым наукам
Рефераты по управленческим наукам
Рефераты по строительным наукам
Психология педагогика
Промышленность производство
Биология и химия
Языкознание филология
Издательское дело и полиграфия
Рефераты по краеведению и этнографии
Рефераты по религии и мифологии
Рефераты по медицине
Рефераты по сексологии
Рефераты по москвоведению
Рефераты по экологии
Краткое содержание произведений
Рефераты по физкультуре и спорту
Топики по английскому языку
Рефераты по математике
Рефераты по музыке
Остальные рефераты
Курсовая работа: Приближенное решение интегрального уравнения
Курсовая работа: Приближенное решение интегрального уравнения
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ
САМАРСКИЙ ГОСУДАРСТВЕННЫЙ АЭРОКОСМИЧЕСКИЙ УНИВЕРСИТЕТ имени академика С. П. Королева
Кафедра высшей математики
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
к курсовой работе по уравнениям математической физики
![]() САМАРА 2009г.
САМАРА 2009г.
Реферат
Курсовая работа: пояснительная записка, 30 страниц, 8 рисунков, 3 источника, 6 таблиц.
Ключевые слова: МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ, МЕТОД ЦЕНТРАЛЬНЫХ РАЗНОСТЕЙ, МЕТОД ПРОГОНКИ, МЕТОД ГАЛЕРКИНА, МЕТОД КОЛЛОКАЦИИ, МЕТОД РИТЦА, МЕТОД ЛИБМАНА, ПРИБЛИЖЕННОЕ РЕШЕНИЕ, МЕТОД СЕТОК, ИНТЕГРАЛЬНОЕ УРАВНЕНИЕ, УРАВНЕНИЕ ТЕПЛОПРОВОДНОСТИ, ВОЛНОВОЕ УРАВНЕНИЕ.
![]() В данной работе требуется с помощью методов
конечно-разностных, центрально-разностных отношений и метода прогонки найти
приближенное решение линейного дифференциального уравнения второго порядка.
Сравнить результаты и сделать выводы.
В данной работе требуется с помощью методов
конечно-разностных, центрально-разностных отношений и метода прогонки найти
приближенное решение линейного дифференциального уравнения второго порядка.
Сравнить результаты и сделать выводы.
Необходимо найти приближенное решение линейного дифференциального уравнения второго порядка с помощью методов Галеркина, Ритца и коллокации. Сравнить результаты, построив графики.
Нужно с помощью метода Либмана отыскать приближенное решение задачи Дирихле в квадрате.
Требуется методом сеток найти приближенное решение первой смешанной задачи для уравнения теплопроводности и для волнового уравнения. Сравнить результаты с аналитическим решением.
Нужно найти приближенное решение интегрального уравнения.
СОДЕРЖАНИЕ
ВВЕДЕНИЕ
I. РЕШЕНИЕ КРАЕВОЙ ЗАДАЧИ
II. МЕТОДЫ ГАЛЕРКИНА, РИТЦА И КОЛЛОКАЦИЙ
III.РЕШЕНИЕ ЗАДАЧИ ДИРИХЛЕ1
IV. ПРИБЛИЖЕННОЕ РЕШЕНИЕ ПЕРВОЙ СМЕШАННОЙ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ НА ОТРЕЗКЕ
V. ПРИБЛИЖЕННОЕ РЕШЕНИЕ ПЕРВОЙ СМЕШАННОЙ ЗАДАЧИ ДЛЯ ВОЛНОВОГО УРАВНЕНИЯ НА ОТРЕЗКЕ
VI. ПРИБЛИЖЕННОЕ РЕШЕНИЕ ИНТЕГРАЛЬНОГО УРАВНЕНИЯ
ЗАКЛЮЧЕНИЕ
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
ВВЕДЕНИЕ
В данной работе требуется с помощью методов конечно-разностных, центрально-разностных отношений и метода прогонки найти приближенное решение линейного дифференциального уравнения второго порядка. Сравнить результаты и сделать выводы.
Необходимо найти приближенное решение линейного дифференциального уравнения второго порядка с помощью методов Галеркина, Ритца и коллокации. Сравнить результаты, построив графики.
Нужно с помощью метода Либмана отыскать приближенное решение задачи Дирихле в квадрате.
Требуется методом сеток найти приближенное решение первой смешанной задачи для уравнения теплопроводности и для волнового уравнения. Сравнить результаты с аналитическим решением.
Нужно найти приближенное решение интегрального уравнения.
I. РЕШЕНИЕ КРАЕВОЙ ЗАДАЧИ
Пусть дано дифференциальное уравнение второго порядка
![]() , (1)
, (1)
где функция ![]() задана
таблично
задана
таблично
| i |
fi(x) |
| 0 | 8,1548 |
| 1 | 6,8925 |
| 2 | 5,8327 |
| 3 | 4,9907 |
| 4 | 4,3818 |
| 5 | 4,0188 |
| 6 | 3,9098 |
| 7 | 4,0581 |
| 8 | 4,4615 |
| 9 | 5,1129 |
| 10 | 6 |
Будем искать решение уравнения (1), удовлетворяющее следующим краевым условиям
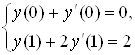 (2)
(2)
Запишем таблицу значений
функций ![]()
| i |
|
|
|
| 0 | 0 | 0 | 0 |
| 1 | 0,1 | -0,2 | 0,03 |
| 2 | 0,2 | -0,4 | 0,12 |
| 3 | 0,3 | -0,6 | 0,27 |
| 4 | 0,4 | -0,8 | 0,48 |
| 5 | 0,5 | -1 | 0,75 |
| 6 | 0,6 | -1,2 | 1,08 |
| 7 | 0,7 | -1,4 | 1,47 |
| 8 | 0,8 | -1,6 | 1,92 |
| 9 | 0,9 | -1,8 | 2,43 |
| 10 | 1 | -2 | 3 |
1. Метод конечных разностей для линейных дифференциальных уравнений второго порядка.
1. Пусть ![]() и значения
и значения ![]() и
и ![]() в каждом узле
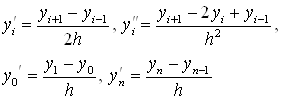
можно записать конечно-разностными отношениями
в каждом узле
можно записать конечно-разностными отношениями
 (3)
(3)
тогда, используя (3), заменим уравнения (1), (2) системой
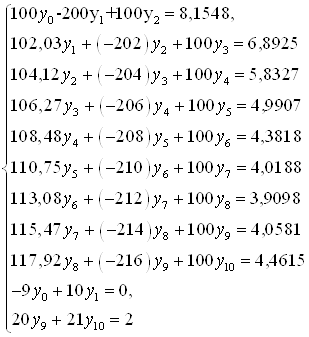 (4)
(4)
Решая систему (4), получим
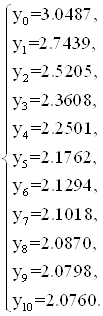
2. Пусть ![]() тогда, используя (3),
заменим уравнения (1), (2) системой:
тогда, используя (3),
заменим уравнения (1), (2) системой:
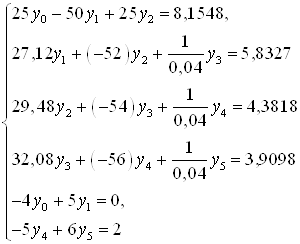 (5)
(5)
Решая систему (5), получим
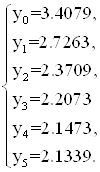
2. Метод центральных разностей для линейных дифференциальных уравнений второго порядка.
1. Пусть ![]() и значения
и значения ![]() и
и ![]() в каждом узле
можно записать центрально-разностными отношениями
в каждом узле
можно записать центрально-разностными отношениями
 (6)
(6)
тогда, используя (6), заменим уравнения (1), (2) системой:
 (7)
(7)
Решая систему (7), получим:

2. Пусть ![]() , тогда, используя (6),
заменим уравнения (1), (2) системой:
, тогда, используя (6),
заменим уравнения (1), (2) системой:
 (8)
(8)
Решая систему (8), получим

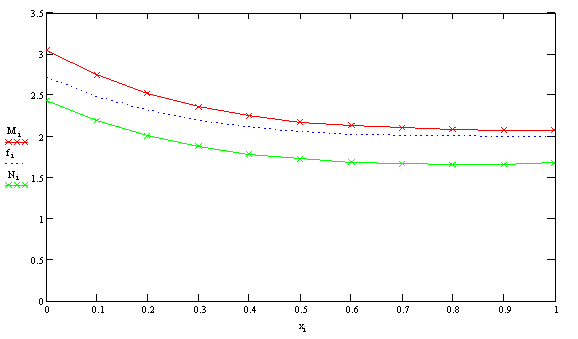
Рис.1-![]() - решение, полученное с
помощью метода конечных разностей (h=0,1),
- решение, полученное с
помощью метода конечных разностей (h=0,1), ![]() - решение, полученное с помощью
метода центральных разностей (h=0,1),
- решение, полученное с помощью
метода центральных разностей (h=0,1),
![]() - точное
решение
- точное
решение
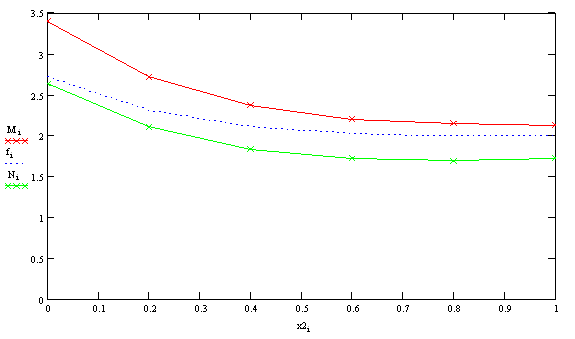
Рис.2-![]() - решение, полученное с
помощью метода конечных разностей (h=0,2),
- решение, полученное с
помощью метода конечных разностей (h=0,2), ![]() - решение , полученное с помощью
метода центральных разностей (h=0,2)
- решение , полученное с помощью
метода центральных разностей (h=0,2)
![]() -точное
решение
-точное
решение
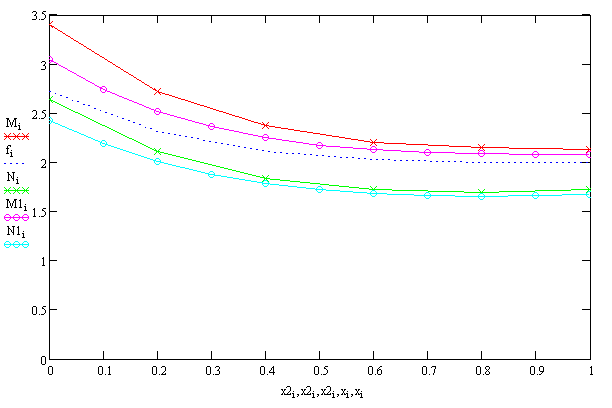
Рис.3- Общий график решений
3. Метод прогонки для линейных дифференциальных уравнений второго порядка.
Конечно-разностные отношения в методе прогонки.
1. Пусть ![]() и значения
и значения ![]() и
и ![]() в каждом узле
можно записать конечно-разностными отношениями:
в каждом узле
можно записать конечно-разностными отношениями:
 (9)
(9)
тогда, используя (20), заменим уравнения (1), (2), (3) системой:
 (10)
(10)
Запишем первые n-1 уравнений в виде:
![]() , где
, где ![]() (11)
(11)
Из системы (21) следует,
что ![]() (12)
(12)
![]() ,
, ![]() вычисляются последовательно, но
при i=0:
вычисляются последовательно, но
при i=0:
![]() (13)
(13)
Остальные ![]() ,
, ![]() вычисляются по формуле:
вычисляются по формуле:
![]() (14)
(14)
Прямой ход вычислений.
По формулам (11) вычисляем
![]() . Далее
вычисляем
. Далее
вычисляем ![]() по
формулам (13) и по рекуррентным формулам (14) находим
по
формулам (13) и по рекуррентным формулам (14) находим ![]() .
.
Обратный ход.
Из уравнения (12) при i=n-2 и из последнего уравнения системы (10) получаем:

Решив эту систему
относительно ![]() , получим
, получим
![]() (15)
(15)
При i=n-2,…,1 используем формулу (12)
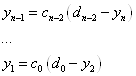
![]() вычисляем из второго уравнения
системы (10)
вычисляем из второго уравнения
системы (10)
![]() (16)
(16)
В результате вычислений получим таблицу:
Таблица №1
| Прямой ход | Обратный ход | ||||||||
| i |
xi |
pi |
qi |
fi |
mi |
ki |
ci |
di |
yi |
| 0 | 0 | 0 | 0 | 8.1548 | -2 | 1 | -1.125 | 0.081548 | 3.049606 |
| 1 | 0.1 | -0.2 | 0.03 | 6.9025 | -2.02 | 1.0203 | -1.14658 | 0.162629 | 2.744645 |
| 2 | 0.2 | -0.4 | 0.12 | 5.8327 | -2.04 | 1.0412 | -1.18177 | 0.252476 | 2.521233 |
| 3 | 0.3 | -0.6 | 0.27 | 4.9907 | -2.06 | 1.0627 | -1.24358 | 0.366984 | 2.361553 |
| 4 | 0.4 | -0.8 | 0.48 | 4.3818 | -2.08 | 1.0848 | -1.36806 | 0.538893 | 2.250789 |
| 5 | 0.5 | -1 | 0.75 | 4.0188 | -2.1 | 1.1075 | -1.70977 | 0.856677 | 2.176909 |
| 6 | 0.6 | -1.2 | 1.08 | 3.9098 | -2.12 | 1.1308 | -5.35913 | 1.695401 | 2.130132 |
| 7 | 0.7 | -1.4 | 1.47 | 4.0581 | -2.14 | 1.1547 | 0.247024 | 10.53205 | 2.10254 |
| 8 | 0.8 | -1.6 | 1.92 | 4.4615 | -2.16 | 1.1792 | -0.40795 | -3.02327 | 2.087729 |
| 9 | 0.9 | -1.8 | 2.43 | 5.1129 | -2.18 | 1.2043 | -0.59217 | -1.43418 | 2.080518 |
| 10 | 1 | -2 | 3 | 6 | -2.2 | 1.23 | -0.67952 | -0.98461 | 2.076684 |
2. Пусть ![]()
В результате вычислений по формулам (9)-(16) получим таблицу:
Таблица №2
| Прямой ход | Обратный ход | ||||||||
| i |
xi |
pi |
qi |
fi |
mi |
ki |
ci |
di |
yi |
| 0 | 0 | 0 | 0 | 8.1548 | -2 | 1 | -1.125 | 0.081548 | 2.048941 |
| 1 | 0.2 | -0.4 | 0.12 | 5.8327 | -2.04 | 1.0412 | -1.15121 | 0.156074 | 1.844047 |
| 2 | 0.4 | -0.8 | 0.48 | 4.3818 | -2.08 | 1.0848 | -1.20313 | 0.247519 | 1.720701 |
| 3 | 0.6 | -1.2 | 1.08 | 3.9098 | -2.12 | 1.1308 | -1.31665 | 0.407622 | 1.650761 |
| 4 | 0.8 | -1.6 | 1.92 | 4.4615 | -2.16 | 1.1792 | -1.64636 | 0.835965 | 1.619574 |
| 5 | 1 | -2 | 3 | 6 | -2.2 | 1.23 | -5.71492 | 5.936293 | 1.63769 |
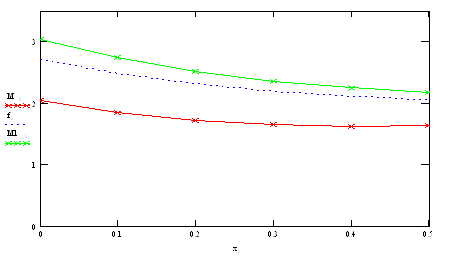
Рис.3-![]() - решение, полученное с
помощью метода прогонки с использованием конечно-разностных отношений (h=0,1),
- решение, полученное с
помощью метода прогонки с использованием конечно-разностных отношений (h=0,1),![]() - решение, полученное с помощью
метода прогонки с использованием конечно разностных отношений (h=0,2) ,
- решение, полученное с помощью
метода прогонки с использованием конечно разностных отношений (h=0,2) , ![]() - точное
решение
- точное
решение
II. Методы Галеркина, Ритца и коллокаций
Пусть дано дифференциальное уравнение второго порядка и его граничные условия
![]() (17)
(17)
1. Метод Галеркина
Введем операторы
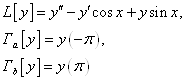
На отрезке [a, b] выберем систему базисных функций
![]()
Проверим систему на ортогональность

Выбранная система
базисных функций является ортогональной и удовлетворяет условию выбора конечной
системы базисных функций ![]()
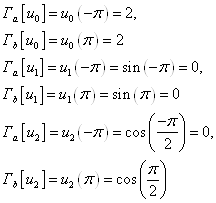
Решение краевой задачи (17) ищется в виде
![]()
1. Рассмотрим решение задачи (17) с двумя базисными функциями:
![]()
Тогда решение
![]()
Рассмотрим выражение
![]() (18)
(18)
Выражение (18) называется невязкой. Для задачи (1) с двумя базисными функциями
![]()
сi выбирается таким образом, чтобы
![]()
Так как ![]() ортогональна ко всем
базисным функциям, то
ортогональна ко всем
базисным функциям, то
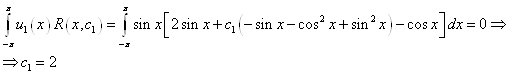
Тогда решение задачи (17)
![]()
2. Рассмотрим решение задачи (17) с тремя базисными функциями
![]()
Тогда решение
![]()
Невязка примет вид
![]()
Коэффициенты с1 и с2 будем искать из системы
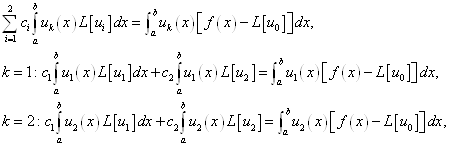
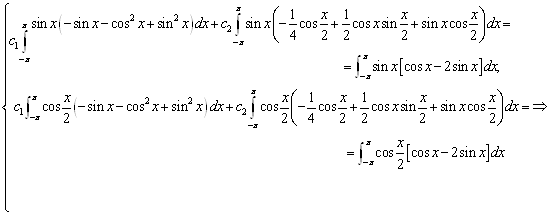
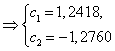
Тогда решение задачи (17)
![]()
2. Метод коллокации
Введем операторы
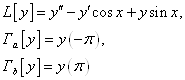
На отрезке [a, b] выберем систему базисных функций
![]()
Будем искать решение задачи (17) в виде
![]()
1. Рассмотрим решение задачи (17) с двумя базисными функциями
![]()
Тогда решение
![]()
Составим невязку
![]()
На отрезке [-π, π] выберем за точку коллокации 0.
![]()
Таким образом, решение задачи (17)
![]() .
.
2. Рассмотрим решение задачи (17) с тремя базисными функциями
![]()
Тогда решение
![]()
Составим невязку
![]()
На отрезке [-π, π]
выберем две точки коллокации: 0 и ![]() . Составим систему уравнений
. Составим систему уравнений

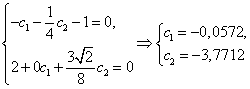
Таким образом, решение задачи (17)
![]()
3. Метод Ритца
Составим функционал по формуле
![]()
![]() (19)
(19)
На отрезке [a, b] выберем систему базисных функций
![]()
Будем искать решение задачи (17) в виде
![]()
Подставим ![]() в (19)
в (19)
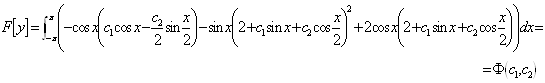
![]()
Составим систему уравнений относительно с1, с2

Таким образом, решение задачи (17)
![]()
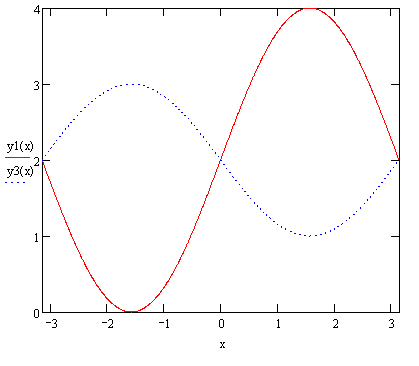
Рис.4- у1(х)-решение, полученное с помощью метода Галеркина (две базисные функции), у2(х)-решение, полученное с помощью метода коллокации (две базисные функции)
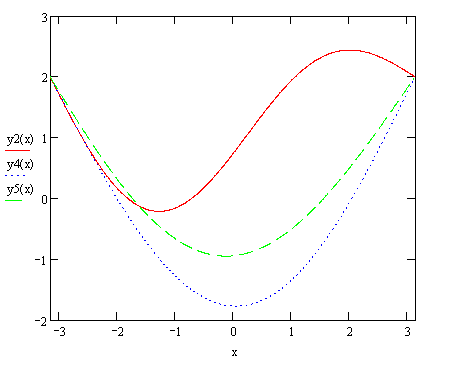
Рис.4-у2(х)- решение, полученное с помощью метода Галеркина (три базисные функции), у4(х)- решение, полученное с помощью метода коллокации (три базисные функции), у5(х)- решение, полученное с помощью метода Ритца (три базисные функции)
Замечание: найти решение методом Ритца для двух базисных функций не удалось, т.к. функция Ф(с1) не квадратична относительно переменной с1 и не удовлетворяет условию существования экстремума
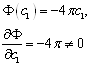
III. Решение задачи Дирихле
Применяя метод сеток с
шагом ![]() ,
найти решение задачи Дирихле в квадрате с вершинами А(0,0), В(0,1), С(1,1), D(1,0).
,
найти решение задачи Дирихле в квадрате с вершинами А(0,0), В(0,1), С(1,1), D(1,0).
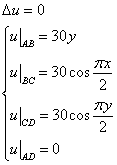 (20)
(20)
1. Метод Либмана
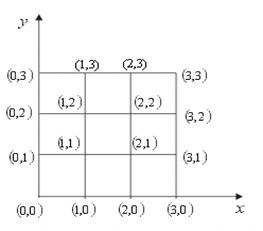
Найдем значения функции ![]() в каждом узле:
в каждом узле:
На АВ
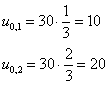
На ВС
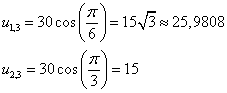
На СD
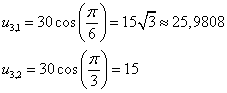
На АD
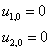
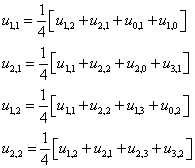
![]()
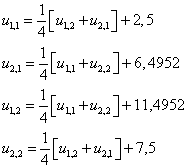
Запишем формулу метода последовательных приближений
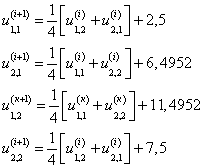
Пусть ![]() , тогда получим
, тогда получим
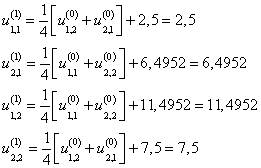
![]()
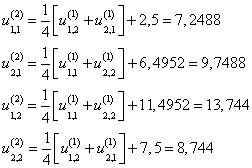
![]()
Таблица №3
| i |
u1,1 |
u1,2 |
u2,1 |
u2,2 |
| 0 | 0 | 0 | 0 | 0 |
| 1 | 2,5 | 11,4952 | 7,5 | 6,4952 |
| 2 | 7,2488 | 13,744 | 9,7488 | 8,744 |
| 3 | 8,3732 | 15,4934 | 11,4982 | 10,4934 |
| 4 | 9,2479 | 16,21185 | 12,21665 | 11,21185 |
| 5 | 9,607125 | 16,61014 | 12,61494 | 11,61014 |
| 6 | 9,806269 | 16,79952 | 12,80432 | 11,79952 |
| 7 | 9,900958 | 16,89665 | 12,90145 | 11,89665 |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
2. Метод Гаусса
Для нахождения точного решения задачи (20) используем метод Гаусса. Для этого решим систему
линейный дифференциальный уравнение
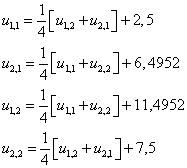 (20*)
(20*)
Введем замену
![]()
Тогда (20*) перепишем в виде
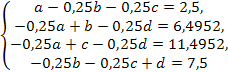
Решая систему, получим
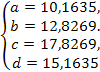
Таким образом, получим точное решение задачи (20)
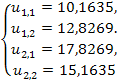
IV. ПРИБЛИЖЕННОЕ РЕШЕНИЕ ПЕРВОЙ СМЕШАННОЙ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ НА ОТРЕЗКЕ
Пусть дано уравнение теплопроводности и его граничные условия
 (21)
(21)
Решим задачу (21), применяя метод сеток для уравнений параболического типа.
1. Пусть ![]() , тогда l=0,02- шаг по оси t, а h=0,2- шаг по оси x. Решение будем искать в виде
, тогда l=0,02- шаг по оси t, а h=0,2- шаг по оси x. Решение будем искать в виде
![]() (22)
(22)
где ![]() (23)
(23)
Получим таблицу:
Таблица №4
| j |
tj/xi |
0 | 0,2 | 0,4 | 0,6 | 0,8 | 1 |
| 0 | 0 | 0 | 0,04 | 0,16 | 0,36 | 0,64 | 1 |
| 1 | 0,02 | 0 | 0,08 | 0,2 | 0,4 | 0,68 | 0,72 |
| 2 | 0,04 | 0 | 0,1 | 0,24 | 0,44 | 0,56 | 0,74 |
| 3 | 0,06 | 0 | 0,12 | 0,27 | 0,4 | 0,59 | 0,61 |
| 4 | 0,08 | 0 | 0,135 | 0,26 | 0,43 | 0,505 | 0,63 |
| 5 | 0,1 | 0 | 0,13 | 0,2825 | 0,3825 | 0,53 | 0,5375 |
| j |
tj/xi |
1,2 | 1,4 | 1,6 | 1,8 | 2 |
|
| 0 | 0 | 0,8 | 0,6 | 0,4 | 0,2 | 0 |
|
| 1 | 0,02 | 0,8 | 0,6 | 0,4 | 0,2 | 0 |
|
| 2 | 0,04 | 0,66 | 0,6 | 0,4 | 0,2 | 0 |
|
| 3 | 0,06 | 0,67 | 0,53 | 0,4 | 0,2 | 0 |
|
| 4 | 0,08 | 0,57 | 0,535 | 0,365 | 0,2 | 0 |
|
| 5 | 0,1 | 0,5825 | 0,4675 | 0,3675 | 0,1825 | 0 |
|
2. Пусть ![]() , тогда l=0,015- шаг по оси t, а h=0,3- шаг по оси x. Решение в виде (22) будем искать по формуле
, тогда l=0,015- шаг по оси t, а h=0,3- шаг по оси x. Решение в виде (22) будем искать по формуле
![]() (24)
(24)
В результате получим таблицу
Таблица №5
| j |
tj/xi |
0 | 0,3 | 0,6 | 0,9 | 1,2 | 1,5 | 1,8 | 2 |
| 0 | 0 | 0 | 0,09 | 0,36 | 0,81 | 0,8 | 0,5 | 0,2 | 0 |
| 1 | 0,015 | 0 | 0,12 | 0,39 | 0,733333 | 0,751667 | 0,5 | 0,216667 | 0 |
| 2 | 0,03 | 0 | 0,145 | 0,402222 | 0,679167 | 0,706667 | 0,494722 | 0,227778 | 0 |
| 3 | 0,045 | 0 | 0,163704 | 0,405509 | 0,637593 | 0,666759 | 0,485556 | 0,234306 | 0 |
| 4 | 0,06 | 0 | 0,176721 | 0,403889 | 0,603773 | 0,631698 | 0,473881 | 0,23713 | 0 |
| 5 | 0,075 | 0 | 0,185129 | 0,399342 | 0,575113 | 0,600741 | 0,460725 | 0,237067 | 0 |
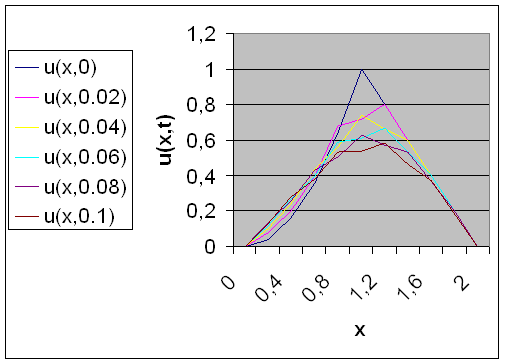
Рис.5- Решение, полученное с помощью метода сеток при
![]()
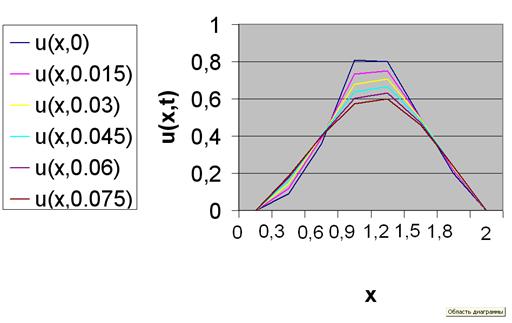
Рис.6- Решение, полученное с помощью метода сеток при
![]()
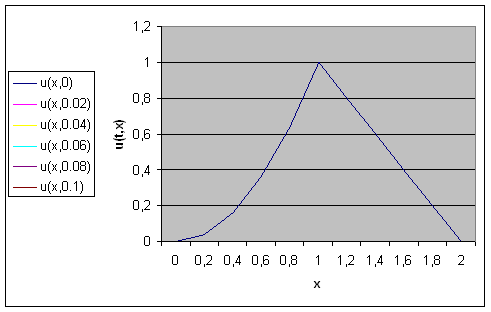
Рис.7- График точного решения, полученного аналитически
V. ПРИБЛИЖЕННОЕ РЕШЕНИЕ ПЕРВОЙ СМЕШАННОЙ ЗАДАЧИ ДЛЯ ВОЛНОВОГО УРАВНЕНИЯ НА ОТРЕЗКЕ
Пусть дано волновое уравнение и его граничные условия
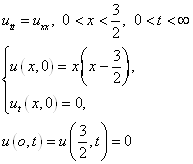 (25)
(25)
Решим задачу (25), применяя метод сеток для уравнений гиперболического типа.
Заменим производные в (25)
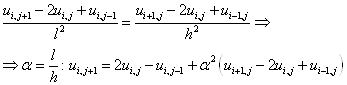
При ![]() (26)
(26)
Пусть ![]() , тогда по формуле (26)
получим
, тогда по формуле (26)
получим
Таблица №6
| j |
tj/xi |
0 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 |
| 0 | 0 | 0 | -0,14 | -0,26 | -0,36 | -0,44 | -0,5 | -0,54 | -0,56 |
| 1 | 0,1 | 0 | -0,14 | -0,26 | -0,36 | -0,44 | -0,5 | -0,54 | -0,56 |
| 2 | 0,2 | 0 | -0,12 | -0,24 | -0,34 | -0,42 | -0,48 | -0,52 | -0,54 |
| 3 | 0,3 | 0 | -0,1 | -0,2 | -0,3 | -0,38 | -0,44 | -0,48 | -0,5 |
| 4 | 0,4 | 0 | -0,08 | -0,16 | -0,24 | -0,32 | -0,38 | -0,42 | -0,44 |
| 5 | 0,5 | 0 | -0,06 | -0,12 | -0,18 | -0,24 | -0,3 | -0,34 | -0,36 |
| j |
tj/xi |
0,8 | 0,9 | 1 | 1,1 | 1,2 | 1,3 | 1,4 | 1,5 |
| 0 | 0 | -0,56 | -0,54 | -0,5 | -0,44 | -0,36 | -0,26 | -0,14 | 0 |
| 1 | 0,1 | -0,56 | -0,54 | -0,5 | -0,44 | -0,36 | -0,26 | -0,14 | 0 |
| 2 | 0,2 | -0,54 | -0,52 | -0,48 | -0,42 | -0,34 | -0,24 | -0,12 | 0 |
| 3 | 0,3 | -0,5 | -0,48 | -0,44 | -0,38 | -0,3 | -0,2 | -0,1 | 0 |
| 4 | 0,4 | -0,44 | -0,42 | -0,38 | -0,32 | -0,24 | -0,16 | -0,08 | 0 |
| 5 | 0,5 | -0,36 | -0,34 | -0,3 | -0,24 | -0,18 | -0,12 | -0,06 | 0 |
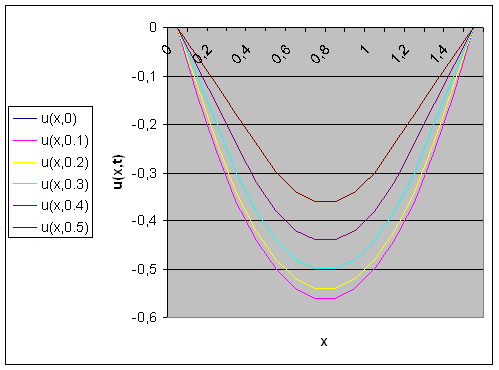
Рис.7- Решение волнового
уравнения методом сеток при ![]()
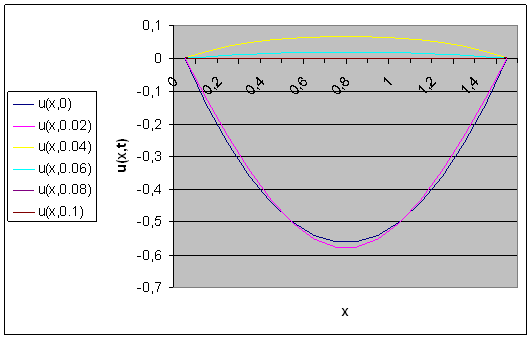
Рис.8- График точного решения, полученного аналитически
VI. ПРИБЛИЖЕННОЕ РЕШЕНИЕ ИНТЕГРАЛЬНОГО УРАВНЕНИЯ
Пусть дано интегральное уравнение
![]() (27)
(27)
Будем искать решение уравнения (27) с помощью метода вырожденных ядер.
Представим ядро![]() в виде ряда
в виде ряда
![]()
Отбросим члены старше пятого порядка
![]()
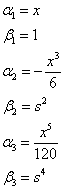
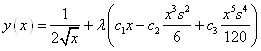

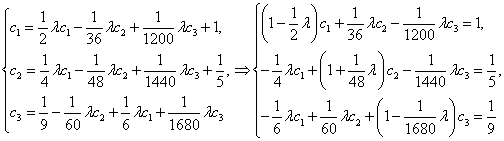
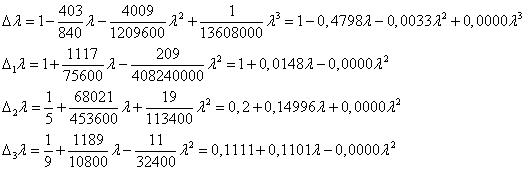
Пусть ![]() , тогда
, тогда
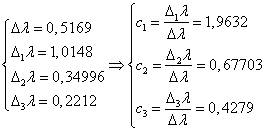
Таким образом, решение задачи (27)
![]()
ЗАКЛЮЧЕНИЕ
![]() В данной работе с помощью методов конечно-разностных,
центрально разностных отношений и метода прогонки найдено приближенное решение
линейного дифференциального уравнения второго порядка. Сравнение результатов
приведено в виде таблиц и графиков.
В данной работе с помощью методов конечно-разностных,
центрально разностных отношений и метода прогонки найдено приближенное решение
линейного дифференциального уравнения второго порядка. Сравнение результатов
приведено в виде таблиц и графиков.
Найдено приближенное решение линейного дифференциального уравнения второго порядка с помощью методов Галеркина, Ритца и коллокации. Сравнение результатов приведено в виде таблиц и графиков.
С помощью метода Либмана получено приближенное решение задачи Дирихле в квадрате. Результаты приведены в виде таблиц.
Методом сеток получены приближенные решения первой смешанной задачи для уравнения теплопроводности и для волнового уравнения. Сравнение результатов с аналитическим решением дано в виде графиков.
Найдено приближенное решение интегрального уравнения.
Список использованных источников
1. В.Ф. Чудесенко Сборник заданий по специальным курсам высшей математики. Типовые расчеты: Учебное пособие. 4-е изд., стер.-СПб.: Издательство «Лань», 2007.- 192с.: ил.- (Учебники для вузов. Специальная литература)
2.Вычислительная математика в примерах и задачах. Н. В. Копченова, И. А. Марон. Главная редакция физико-математической литературы изд-ва: Наука, М., 1972.
3. Тихонов, Самарский "Уравнения математической физики", М.: Наука, 1967.