Курсовая работа: Некоторые уравнения математической физики в частных производных

Федеральное агентство по образованию

ГОУ "Ульяновский государственный педагогический университет им. И. Н. Ульянова"

Кафедра математического анализа

"Некоторые уравнения математической физики в частных производных"

Ульяновск, 2008 г.

Содержание

Введение

Глава 1. Уравнения гиперболического типа

1.1 Задачи, приводящие к уравнениям гиперболического типа

1.2 Уравнение колебаний струны

1.3 Метод разделения переменных. Уравнение свободных колебаний струны

1.4 Решение уравнений

Глава 2. Уравнения параболического типа

2.1 Уравнение распространения тепла в стержне

2.2 Решение задач

Заключение

Литература

Введение

Изучением дифференциальных уравнений в частных производных занимается математическая физика. Основы теории этих уравнений впервые были изложены в знаменитом "Интегральном исчислении" Л. Эйлера.

Классические уравнения математической физики являются линейными. Особенность линейных уравнений состоит в том, что если U и V – два решения, то функция aU + bV при любых постоянных a и b снова является решением. Это обстоятельство позволяет построить общее решение линейного дифференциального уравнения из фиксированного набора его элементарных решений и упрощает теорию этих уравнений.

Современная общая теория дифференциальных уравнений занимается главным образом линейными уравнениями и специальными классами нелинейных уравнений. Основным методом решения нелинейных дифференциальных уравнений в частных производных выступает численное интегрирование.

Круг вопросов математической физики тесно связан с изучением различных физических процессов. Сюда относятся явления, изучаемые в гидродинамике, теории упругости, электродинамике и т.д. Возникающие при этом математические задачи содержат много общих элементов и составляют предмет математической физики.

Постановка задач математической физики, будучи тесно связанной с изучением физических проблем, имеет свои специфические черты. Так, например, начальная и конечная стадии процесса носят качественно различный характер и требуют применения различных математических методов.

Круг вопросов, относящихся к математической физике, чрезвычайно широк. В данной работе рассматриваются задачи математической физики, приводящие к уравнениям с частными производными.

Расположение материала соответствует основным типам уравнений. Изучение каждого типа уравнений начинается с простейших физических задач, приводящих к уравнениям рассматриваемого типа.

Глава 1. Уравнения гиперболического типа

1.1 Задачи, приводящие к уравнениям гиперболического типа

Уравнения с частными производными 2-го порядка гиперболического типа наиболее часто встречаются в физических задачах, связанных с процессами колебаний. Простейшее уравнение гиперболического типа

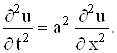
называется волновым уравнением. К исследованию этого уравнения приводит рассмотрение процессов поперечных колебаний струны, продольных колебаний стержня, электрических колебаний в проводе, крутильных колебаний вала, колебаний газа и т.д.

1.2 Уравнение колебаний струны

В математической физике под струной понимают гибкую, упругую нить. Напряжения, возникающие в струне в любой момент времени, направлены по касательной к ее профилю. Пусть струна длины в начальный момент направлена по отрезку оси Оx от 0 до . Предположим, что концы струны закреплены в точках . Если струну отклонить от ее первоначального положения, а потом предоставить самой себе или, не отклоняя струны, придать в начальный момент ее точкам некоторую скорость, или отклонить струну и придать ее точкам некоторую скорость, то точки струны будут совершать движения – говорят, что струна начнет колебаться. Задача заключается в определении формы струны в любой момент времени и определении закона движения каждой точки струны в зависимости от времени.

Будем рассматривать малые отклонения точек струны от начального положения. В силу этого можно предполагать, что движение точек струны происходит перпендикулярно оси Ox и в одной плоскости. При этом предположении процесс колебания струны описывается одной функцией , которая дает величину перемещения точки струны с абсциссой x в момент t.

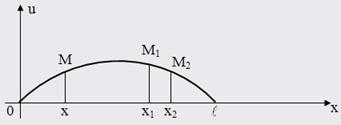
Рис. 1.1.

Так как мы рассматриваем малые отклонения струны в плоскости , то будем предполагать, что длина элемента струны равняется ее проекции на ось Ox, т.е. Также будем предполагать, что натяжение во всех точках струны одинаковое; обозначим его через Т.

Рассмотрим элемент струны .

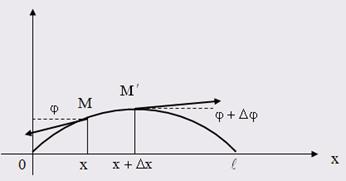
Рис. 1.2.

На концах этого элемента, по касательным к струне, действуют силы Т. Пусть касательные образуют с осью Ox углы . Тогда проекция на ось Ou сил, действующих на элемент , будет равна . Так как угол мал, то можно положить , и мы будем иметь:

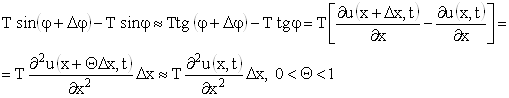
(здесь мы применили теорему Лагранжа к выражению, стоящему в квадратных скобках).

Чтобы получить уравнение движения, нужно внешние силы, приложенные к элементу, приравнять силе инерции. Пусть - линейная плотность струны. Тогда масса элемента струны будет . Ускорение элемента равно . Следовательно, по принципу Даламбера будем иметь:

Сокращая на и обозначая , получаем уравнение движения

.(1)

Это и есть волновое уравнение – уравнение колебаний струны. Для полного определения движения струны одного уравнения (1) недостаточно. Искомая функция должна удовлетворять еще граничным условиям, указывающим, что делается на концах струны , и начальным условиям, описывающим состояние струны в начальный момент (t = 0). Совокупность граничных и начальных условий называется краевыми условиями.

Пусть, например, как мы предполагали, концы струны при неподвижны. Тогда при любом t должны выполнятся равенства:

(2’)

(2’’)

Эти равенства являются граничными условиями для нашей задачи.

В начальный момент t = 0 струна имеет определенную форму, которую мы ей придали. Пусть эта форма определяется функцией f (x). Таким образом, должно быть

(3’)

Далее, в начальный момент должна быть задана скорость в каждой точке струны, которая определяется функцией . Таким образом, должно быть

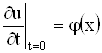(3’’)

Условия (3’) и (3’’) являются начальными условиями.

Замечание. В частности, может быть или . Если же и , то струна будет находится в покое, следовательно, .

1.3 Метод разделения переменных. Уравнение свободных колебаний струны

Метод разделения переменных или метод Фурье, является одним из наиболее распространенных методов решения уравнений с частными производными. Изложение этого метода мы проведем для задачи о колебаниях струны, закрепленной на концах. Итак, будем искать решение уравнения

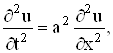
удовлетворяющее однородным граничным условиям

(9)

и начальным условиям

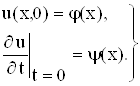(10)

Уравнение (1) линейно и однородно, поэтому сумма частных решений также является решением этого уравнения. Имея достаточно большое число частных решений, можно попытаться при помощи суммирования их с некоторыми коэффициентами найти искомое решение.

Поставим основную вспомогательную задачу: найти решение уравнения

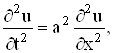
не равное тождественно нулю, удовлетворяющее однородным граничным условиям

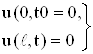(11)

и представимое в виде произведения

(12)

где X (x) – функция только переменного x, T (t) – функция только переменного t.

Подставляя предполагаемую форму решения (12) в уравнение (1), получим:

или, после деления на XT,

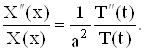(13)

Чтобы функция (12) была решением уравнения (1), равенство (13) должно удовлетворяться тождественно, т. е. 0 ‹ х ‹ , t › 0. Правая часть равенства (13) является функцией только переменного t, а левая – только х. Фиксируя, например, некоторое значение х и меняя t (или наоборот), получим, что правая и левая части равенства (13) при изменении своих аргументов сохраняют постоянное значение

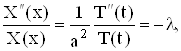(14)

где – постоянная, которую для удобства последующих выкладок берем со знаком минус, ничего не предполагая при этом о ее знаке.

Из соотношения (14) получаем обыкновенные дифференциальные уравнения для определения функций X (x) и T (t)

(15)

(16)

Граничные условия (11) дают:

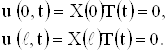
Отсюда следует, что функция X (x) должна удовлетворять дополнительным условиям:

X(0) = X() = 0, (17)

Так как иначе мы имели бы

в то время как задача состоит в нахождении нетривиального решения. Для функции T (t) в основной вспомогательной задаче никаких дополнительных условий нет.

Таким образом, в связи с нахождением функции X (x) мы приходим к простейшей задаче о собственных значениях: найти те значения параметра , при которых существуют нетривиальные решения задачи:

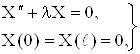(18)

а также найти эти решения. Такие значения параметра называются собственными значениями, а соответствующие им нетривиальные решения – собственными функциями задачи (18). Сформулированную таким образом задачу часто называют задачей Штурма – Лиувилля.

Рассмотрим отдельно случаи, когда параметр отрицателен, равен нулю или положителен.

1. При ‹ 0 задача не имеет нетривиальных решений. Действительно, общее решение уравнения (15) имеет вид

Граничные условия дают:

Х (0) = С1 + С2 = 0;

т. е.

Но в рассматриваемом случае – действительно и положительно, так что . Поэтому

С1 =0, С2 = 0

и, следовательно,

Х (х)0.

2. При = 0 также не существует нетривиальных решений. Действительно, в этом случае общее решение уравнения (15) имеет вид

Х (х) = С1х + С2.

Граничные условия дают:

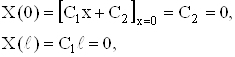
т. е. С1 = 0 и С2 = 0 и, следовательно,

Х (х)0.

3. При › 0 общее решение уравнения может быть записано в виде

Граничные условия дают:

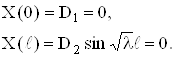
Если Х(х) не равно тождественно нулю, то D20, поэтому

(19)

Или

где n- любое целое число. Следовательно, нетривиальные решения задачи (18) возможны лишь при значениях

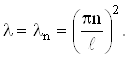
Этим собственным значениям соответствуют собственные функции

где Dn – произвольная постоянная.

Итак, только при значениях , равных

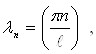(20)

существуют нетривиальные решения задачи (11)

(21)

определяемые с точностью до произвольного множителя, который мы положили равным единице. Этим же значениям n соответствуют решения уравнения (9)

(22)

где An и Bn – произвольные постоянные.

Возвращаясь к задаче (1), (9), (10), заключаем, что функции

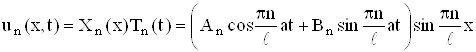(23)

являются частными решениями уравнения (1), удовлетворяющими граничным условиям (11) и представимыми в виде произведения (12) двух функций, одна из которых зависит только от х, другая – от t. Эти решения могут удовлетворить начальным условиям (10) нашей исходной задачи только для частных случаев начальных функций j(x) и y(x).

Обратимся к решению задачи (1), (9), (10) в общем случае. В силу линейности и однородности уравнения (1) сумма частных решений

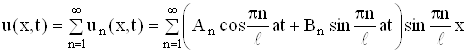(24)

также удовлетворяет этому уравнению и граничным условиям (9). Начальные условия позволяют определить An и Bn. Потребуем, чтобы функция (24) удовлетворяла условиям (10)

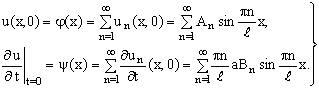(25)

Из теории рядов Фурье известно, что произвольная кусочно-непрерывная и кусочно-дифференцируемая функция f(x), заданная в промежутке , разлагается в ряд Фурье

(26)

где

(27)

Если функции j(x) и y(x) удовлетворяют условиям разложения в ряд Фурье, то

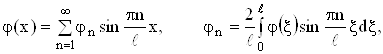(28)

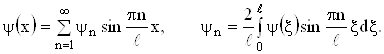(29)

Сравнение этих рядов с формулами (25) показывает, что для выполнения начальных условий надо положить

(30)

чем полностью определяется функция (24), дающая решение исследуемой задачи.

Итак, мы доказали, что ряд (24), где коэффициенты An и Bn определены по формуле (30), если он допускает двукратное почленное дифференцирование, представляет функцию u (x, t), которая является решением уравнения (1) и удовлетворяет граничным и начальным условиям (9) и (10).

Замечание. Решая рассмотренную задачу для волнового уравнения другим методом, можно доказать, что ряд (24) представляет решение и в том случае, когда он не допускает почленного дифференцирования. При этом функция должна быть дважды дифференцируемой, а - один раз дифференцируемой.

1.4 Решение уравнений

1. Найти решение уравнения:

, если , .

Решение:

Так как , а , то

где . Таким образом, , или .

2. Найти форму струны, определяемой уравнением в момент , если

3. , .

Решение:

Имеем

т.е.

, или .

Если , то , т.е. струна параллельна оси абсцисс.

4. Струна, закрепленная на концах и , имеет в начальный момент форму параболы .

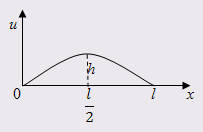
5. Определить смещение точек струны от оси абсцисс, если начальные скорости отсутствуют.

Решение:

Здесь , . Находим коэффициенты ряда, определяющего решение уравнения колебания струны:

; .

Для нахождения коэффициента дважды интегрируем по частям:

, , , ;

т.е.

, , , ;

Подставляя выражения для и получим:

Если , то , а если , то ; поэтому окончательно имеем

Пусть начальные отклонения струны, закрепленной в точках и , равны нулю, а начальная скорость выражается формулой

Определить форму струны для любого момента времени t.

Решение:

Здесь , а в интервале , и вне этого интервала.

Следовательно, ;

Отсюда

Или

Глава 2. Уравнения параболического типа

2.1 Уравнение распространения тепла в стержне

Рассмотрим однородный стержень длины . Будем предполагать, что боковая поверхность стержня теплонепроницаема и что во всех точках поперечного сечения стержня температура одинакова. Изучим процесс распространения тепла в стержне.

Расположим ось Ох так, что один конец стержня будет совпадать с точкой х = 0, а другой – с точкой х = .

Рис. 2.1.

Пусть u (x, t) – температура в сечении стержня с абсциссой х в момент t. Опытным путем установлено, что скорость распространения тепла, т. е. количество тепла, протекающего через сечение с абсциссой х за единицу времени, определяется формулой

(1)

где S – площадь сечения рассматриваемого стержня, k – коэффициент теплопроводности.

Рассмотрим элемент стержня, заключенный между сечениями с абсциссами х1 и х2 (х2 – х1 = х). Количество тепла, прошедшего через сечение с абсциссой х1 за время t, будет равно

(2)

то же самое с абсциссой х2:

(3)

Приток Q1 - Q2 в элемент стержня за время t будет равняться:

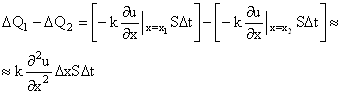(4)

Этот приток тепла за время t затратился на повышение температуры элемента стержня на величину u:

Или

(5)

где с – теплоемкость вещества стержня, – плотность вещества стержня (xS – масса элемента стержня).

Приравнивая выражения (4) и (5) одного и того же количества тепла , получим:

(6)

Это и есть уравнение распространения тепла (уравнение теплопроводности) в однородном стержне.

Чтобы решение уравнения (6) было вполне определено, функция u (x, t) должна удовлетворять краевым условиям, соответствующим физическим условиям задачи. Краевые условия для решения уравнения (6) могут быть различные. Условия, которые соответствуют так называемой первой краевой задаче для , следующие:

u (x, 0) = φ(x), (7)

u (0, t) = ψ1(t), (8)

u (, t) = ψ2(t). (9)

Физическое условие (7) (начальное условие) соответствует тому, что при в разных сечениях стержня задана температура, равная φ(x). Условия (8) и (9) (граничные условия) соответствуют тому, что на концах стержня при х = 0 и при х = поддерживается температура, равная ψ1(t) и ψ2(t) соответственно.

Доказывается, что уравнение (6) имеет единственное решение в области , удовлетворяющее условиям (7) – (9).

2.2 Решение задач

1. Задача:

Решить уравнение

Решение. Составим и решим систему уравнений характеристик

Уравнение даёт первый интеграл . Преобразуем три дроби , используя правило работы с равными дробями:

Отсюда получим второй первый интеграл

Возьмём следующее уравнение , подставим и в это уравнение, получим

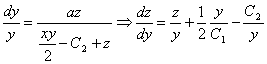Решим полученное линейное уравнение:

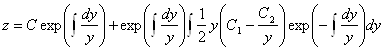Получим третий первый интеграл

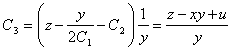2. Задача

Найти общее решение уравнения

Решение: Составим и решим систему уравнений характеристик

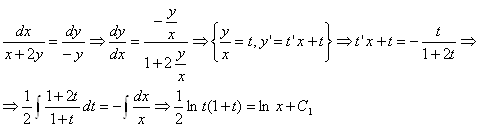
Первый интеграл равен . Функция вида , где - произвольная дифференцируемая функция, является общим решением уравнения.

3. Задача

Решить уравнение

Решение. Составим систему уравнений характеристик

Первая пара дробей даёт первый интеграл

Подставим во вторую пару дробей, получим

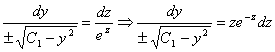Интегрируя последнее уравнение, получим второй первый интеграл

Общее решение имеет вид

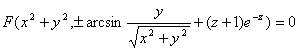4. Задача

Решение задачу Коши

Решение. Найдем два первых интеграла. Составим систему

гиперболический колебание дифференциальный теплопроводность интеграл

Отсюда получим первый интеграл .

Решая уравнение при условии, что , получим второй первый интеграл

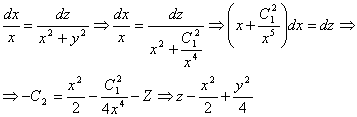
Подставим в два первых интеграла:

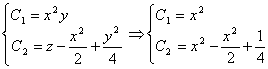
Исключая из этой пары равенств, получим связь между первыми интегралами . Подставляя вместо и первые интегралы, получим решение задачи Коши:

5. Задача

Решить задачу Коши , .

Решение. Найдем первые интегралы системы уравнений характеристики ; они равны

, .

Найдём, используя начальные данные, связь между первыми интегралами:

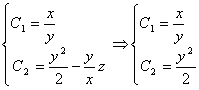
Подставим первые интегралы и , получим решение:

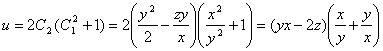6. Решить уравнение для следующего начального распределения температуры стержня:

Решение: Стержень является бесконечным, поэтому решение запишется в виде интеграла Пуассона:

Так как в интервале равна постоянной температуре , а вне интервала температура равна нулю, то решение примет вид

Полученный результат можно преобразовать к интегралу вероятностей:

Действительно полагая , , получим

Таким образом, решение выразится формулой

Графиком функции является кривая:

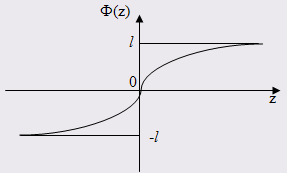
Найти решение уравнения , удовлетворяющее начальному условию и краевому условию .

Решение: Здесь мы имеем дифференциальное уравнение теплопроводности для полубесконечного стержня. Решение, удовлетворяющее указанным условиям, имеет вид

Или

Полагая , , преобразуем первый интеграл, пользуясь интегралом вероятностей, т.е.

Полагая , , получим

Таким образом, решение принимает вид

Заключение

В курсовой работе приведены некоторые примеры применения дифференциальных уравнений для моделирования таких реальных процессов, как колебания струны, распространение тепла в стержне.

Работа начинается с рассмотрения простейших задач, приводящих к дифференциальным уравнениям гиперболического типа (колебания струны, электрические колебания в проводах). Затем рассматривается один из методов решения уравнений данного типа. Во второй главе рассматриваются дифференциальные уравнения параболического типа (распространение тепловых волн) и одно из приложений к данной сфере – температурные волны.

Вследствие большого объема теории по применению дифференциальных уравнений для моделирования реальных процессов в данной курсовой работе не мог быть рассмотрен весь материал.

В заключение хотелось бы отметить особую роль дифференциальных уравнений при решении многих задач математики, физики и техники, так как часто не всегда удается установить функциональную зависимость между искомыми и данными переменными величинами, но зато удается вывести дифференциальное уравнение, позволяющее точно предсказать протекание определенного процесса при определенных условиях.

Литература

1. Н. С. Пискунов "Дифференциальное и интегральное исчисления", М., "Наука", 1972, том. 2.

2. И. М. Уваренков, М. З. Маллер "Курс математического анализа", М., "Просвещение", 1976.

3. А. Н. Тихонов, А. А. Самарский "Уравнения математической физики", М., "Наука", 1972.

4. Владимиров В. С. "Уравнения математической физики", М., "Наука", 1988.