
Рефераты по рекламе
Рефераты по философии
Рефераты по финансам
Рефераты по химии
Рефераты по цифровым устройствам
Рефераты по экологическому праву
Рефераты по экономико-математическому моделированию
Рефераты по экономической географии
Рефераты по экономической теории
Рефераты по этике
Рефераты по юриспруденции
Рефераты по языковедению
Рефераты по юридическим наукам
Рефераты по истории
Рефераты по компьютерным наукам
Рефераты по медицинским наукам
Рефераты по финансовым наукам
Рефераты по управленческим наукам
Рефераты по строительным наукам
Психология педагогика
Промышленность производство
Биология и химия
Языкознание филология
Издательское дело и полиграфия
Рефераты по краеведению и этнографии
Рефераты по религии и мифологии
Рефераты по медицине
Рефераты по сексологии
Рефераты по москвоведению
Рефераты по экологии
Краткое содержание произведений
Рефераты по физкультуре и спорту
Топики по английскому языку
Рефераты по математике
Рефераты по музыке
Остальные рефераты
Курсовая работа: Модели и методы принятия решений
Курсовая работа: Модели и методы принятия решений
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ОТКРЫТЫЙ УНИВЕРСИТЕТ
ФАКУЛЬТЕТ ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ
Курсовая работа
Модели и методы принятия решений
Выполнила: Токарева О.П.
Заочная форма обучения
Курс V
Специальность 210100
№ зачетной книжки 602654
Проверил: Цыганов Ю.К.
Москва
2008
Задание
на курсовую работу по дисциплине «Модели и методы принятия решений»
Вариант 4
Задача 1.
Решить графоаналитическим методом.
min j (X) = – 3x1 – 2x2
при 2x1 + x2 ³ 2
x1 + x2 £ 3
– x1 + x2 ³ 1
X ³ 0
Задача 2.
· Найти экстремумы методом множителей Лагранжа.
· Решение проиллюстрировать графически.
extr j (X) = x12 + x22
при x12 + x22 – 9x2 + 4,25 = 0
Задача 3.
· Решить на основе условий Куна-Таккера.
· Решение проиллюстрировать графически.
extr j (X) = x1x2
при 6x1 + 4x2 ³ 12
2x1 + 3x2 £ 24
– 3x1 + 4x2 £ 12
Задача 4.
· Получить выражение расширенной целевой функции (РЦФ) и составить блок-схему алгоритма численного решения задачи методом штрафных функций в сочетании с одним из методов безусловной минимизации.
· Решить задачу средствами MS Excel.
· Решение проиллюстрировать графически.
max j (X) = 2x1 + 4x2 – x12 – 2x22
при x1 + 2x2 £ 8
2x1 – x2 £ 12
X ³ 0
Задача 1
Решить графоаналитическим методом.
min j (X) = – 3x1 – 2x2
при 2x1 + x2 ³ 2
x1 + x2 £ 3
– x1 + x2 ³ 1
X ³ 0
Решение:
Построим линии ограничений:
Примем: 2х1+х2=2 (a)
х1+х2=3 (b)
-х1+х2=1 (c)
экстремум функция минимизация алгоритм
Получаем три прямые a, b и c, которые пересекаются и образуют треугольник соответствующий области которая соответствует первым трем ограничениям, добавляя четвертое ограничение получаем четырехугольник ABCD – допустимая область значений, в которой надо искать минимум (на рисунке эта область не заштрихована).
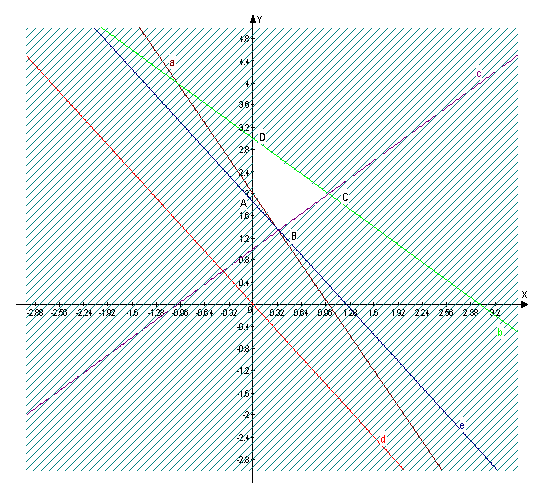
Рис. 1
Примем целевую функцию равной нулю (красная линия d) тогда градиент имеет координаты (-3;-2). Для того, чтобы найти минимум целевой функции будем перемещать график линии d параллельно самой себе в направлении антиградиента до входа ее в область ограничений. Точка в которой область войдет в допустимую область и будет искомой точкой минимума целевой функции. Это точка В(0,33 ; 1,33). При этом целевая функция будет иметь значение:
![]()
Темно-синяя линия на рисунке (е).
Задача 2.
· Найти экстремумы методом множителей Лагранжа.
· Решение проиллюстрировать графически.
extr j (X) = x12 + x22
при x12 + x22 – 9x2 + 4,25 = 0
Решение:
Составим функцию Лагранжа
h(X)=x12 + x22 - 9x2 + 4,25=0
![]()
Составим систему уравнений из частных производных и приравняем их к нулю:

Решим данную систему уравнений:
Разложим на множители 1 уравнение системы:
![]()
Предположим, что ![]() , тогда
, тогда ![]() . Подставим во
второе уравнение:
. Подставим во
второе уравнение:
2x2 - 2x2 + 9 = 0
9 = 0 не верно, следовательно принимаем, что
![]() , а
, а ![]()
Подставляем ![]() в третье
уравнение:
в третье
уравнение:
![]()
Решая это квадратное уравнение получаем, что
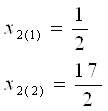
Подставляем эти значения во второе уравнение:
1.Подставим первый корень
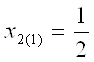 , получаем
, получаем

2. Подставим второй
корень 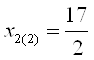 ,
получаем
,
получаем
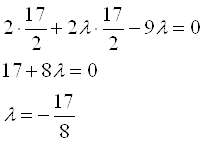
|
( X*,λ*) N |
X1* | X2* | λ* | φ(X*) | Примечание |
| 1 | 0 |
|
|
|
Min |
| 2 | 0 |
|
|
|
Max |
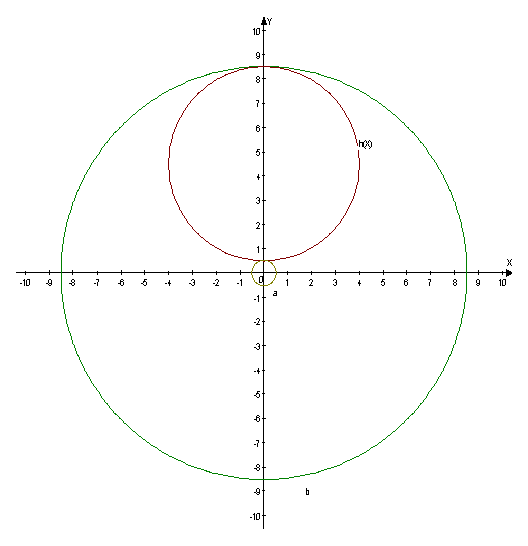
![]() - кривая a (окружность)
- кривая a (окружность)
![]() - кривая b (окружность)
- кривая b (окружность)
Задача 3
· Решить на основе условий Куна-Таккера.
· Решение проиллюстрировать графически.
extr j (X) = x1x2
при 6x1 + 4x2 ³ 12
2x1 + 3x2 £ 24
– 3x1 + 4x2 £ 12
Решение:
Решим задачу на основе условий Куна-Таккера.
Составим функцию Лагранжа:
![]()
Составим систему уравнений из частных производных и приравняем их к нулю:

Решим данную систему уравнений:
1.Предположим, что![]() , тогда из
уравнения 5 получим:
, тогда из
уравнения 5 получим:
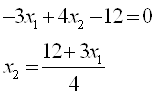
Предположим, что ![]() ,
,![]() ,
,![]() , тогда из уравнения 1
получим:
, тогда из уравнения 1
получим:
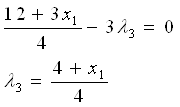
Пусть ![]() , тогда из уравнения 2
получаем:
, тогда из уравнения 2
получаем:
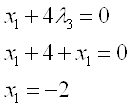
Это решение не удовлетворяет условиям задачи: (Х≥0)
2.Предположим, что ![]() и
и ![]() , тогда из
уравнения 1 получим:
, тогда из
уравнения 1 получим:
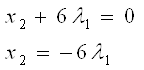
Предположим, что ![]() ,
, ![]() ,
, ![]() , выразим из
второго уравнения
, выразим из
второго уравнения ![]() :
:
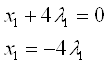
Подставим в 3 уравнение:
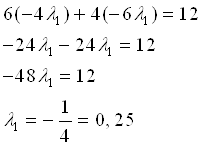
Получаем:![]() ,
, ![]() ,
, ![]()
В этой точке функция ![]() равна
минимальному значению
равна
минимальному значению
3. Предположим, что ![]() ,
, ![]() и
и ![]() , тогда из
второго уравнения получим:
, тогда из
второго уравнения получим:
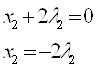
Предположим, что ![]() ,
,![]() и
и ![]() , тогда из второго
уравнения следует:
, тогда из второго
уравнения следует:
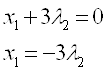
Подставим в четвертое уравнение:
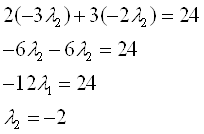
Получаем: ![]() ,
, ![]() ,
, ![]()
В этой точке функция ![]() имеет
максимальное значение:
имеет
максимальное значение:
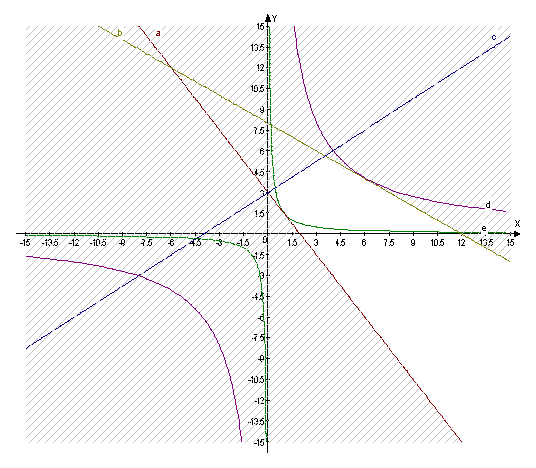
|
X* N |
X1* | X2* | φ(X*) | Примечание |
| 1 | 1 | 1,5 | 1,5 | Min |
| 2 | 6 | 4 | 24 | Max |
Прямая а соответствует графику функции 6х1+4х2=12
Прямая b – графику функции 2х1+3х2=24
Прямая с – графику функции -3х1+4х2=12
Прямая d – графику функции ![]()
Прямая е – графику
функции![]()
Задача 4
· Получить выражение расширенной целевой функции (РЦФ) и составить блок-схему алгоритма численного решения задачи методом штрафных функций в сочетании с одним из методов безусловной минимизации.
· Решить задачу средствами MS Excel.
· Решение проиллюстрировать графически.
max j (X) = 2x1 + 4x2 – x12 – 2x22
при x1 + 2x2 £ 8
2x1 – x2 £ 12
X ³ 0
Решение:
1. Найдем выражение вектор функции системы:
Составим функцию Лагранжа:
![]()
Вектор функция системы:

2. Составим матрицу Якоби
 =
=