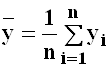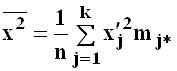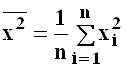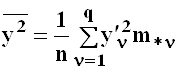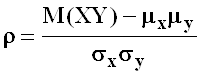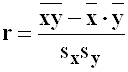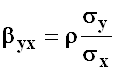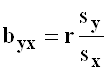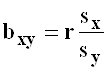Рефераты по рекламе
Рефераты по философии
Рефераты по финансам
Рефераты по химии
Рефераты по цифровым устройствам
Рефераты по экологическому праву
Рефераты по экономико-математическому моделированию
Рефераты по экономической географии
Рефераты по экономической теории
Рефераты по этике
Рефераты по юриспруденции
Рефераты по языковедению
Рефераты по юридическим наукам
Рефераты по истории
Рефераты по компьютерным наукам
Рефераты по медицинским наукам
Рефераты по финансовым наукам
Рефераты по управленческим наукам
Рефераты по строительным наукам
Психология педагогика
Промышленность производство
Биология и химия
Языкознание филология
Издательское дело и полиграфия
Рефераты по краеведению и этнографии
Рефераты по религии и мифологии
Рефераты по медицине
Рефераты по сексологии
Рефераты по москвоведению
Рефераты по экологии
Краткое содержание произведений
Рефераты по физкультуре и спорту
Топики по английскому языку
Рефераты по математике
Рефераты по музыке
Остальные рефераты
Контрольная работа: Корреляционный анализ
Контрольная работа: Корреляционный анализ
Корреляционный анализ
Корреляционный анализ - математико-статистический метод выявления взаимозависимости компонент многомерной случайной величины и оценки тесноты их связи.
Предпосылки корреляционного анализа
При построении корреляционных моделей
исходят из выполнения условий случайности результатов наблюдений и нормальности
закона распределения анализируемой h-мерной генеральной совокупности, что обеспечивает линейный характер изучаемой
зависимости между наблюдаемыми признаками ![]() и
позволяет использовать в качестве показателей силы стохастической (вероятностной)
связи парные, частные и множественные коэффициенты корреляции и детерминации.
и
позволяет использовать в качестве показателей силы стохастической (вероятностной)
связи парные, частные и множественные коэффициенты корреляции и детерминации.
Понятие "корреляционная зависимость"
В статистических исследованиях выделяют два вида связи между случайными величинами: функциональную и стохастическую.
Зависимость признаков ![]() называется
функциональной, если каждое наблюдаемое значение
называется
функциональной, если каждое наблюдаемое значение ![]() зависимой
переменной
зависимой
переменной ![]() однозначно определяется по
полученным в том же самом наблюдении значениям
однозначно определяется по
полученным в том же самом наблюдении значениям ![]() остальных
переменных
остальных
переменных ![]() согласно некоторому правилу:
согласно некоторому правилу:
![]() , единому для всех
наблюдений.
, единому для всех
наблюдений.
Стохастической зависимостью переменной ![]() от переменных
от переменных ![]() называется такое отношение
между случайными величинами
называется такое отношение
между случайными величинами ![]() , при
котором каждой реализации
, при
котором каждой реализации ![]() случайного
вектора
случайного
вектора ![]() однозначно соответствует
некоторое условное распределение вероятностей случайной величины
однозначно соответствует
некоторое условное распределение вероятностей случайной величины ![]() , при этом, по крайней
мере, двум возможным различным реализациям отвечают неодинаковые распределения.
, при этом, по крайней
мере, двум возможным различным реализациям отвечают неодинаковые распределения.
В отличие от функциональной зависимости, когда каждому
набору значений объясняющих переменных ![]() соответствует
только одно значение объясняемой переменной
соответствует
только одно значение объясняемой переменной ![]() ,
при стохастической зависимости любой допустимой совокупности значений
,
при стохастической зависимости любой допустимой совокупности значений ![]() отвечает множество
возможных значений зависимой переменной
отвечает множество
возможных значений зависимой переменной ![]() .
.
Корреляционной зависимостью переменной ![]() от переменных
от переменных ![]() называется функциональная
зависимость условного математическим ожидания
называется функциональная
зависимость условного математическим ожидания ![]() случайной
величины
случайной
величины ![]() от реализации
от реализации ![]() случайного вектора
случайного вектора ![]() .
.
Корреляционная зависимость является лишь одной из частных форм стохастической связи между случайными величинами и не исчерпывает в общем случае весь объем понятия "стохастическая зависимость".
Функция ![]() ,
устанавливающая зависимость условного математического ожидания
,
устанавливающая зависимость условного математического ожидания ![]() от возможных значений
от возможных значений ![]() случайных величин
случайных величин ![]() , называется функцией
регрессии случайной величины
, называется функцией
регрессии случайной величины ![]() на
случайный вектор
на
случайный вектор ![]() .
.
Если функция регрессии ![]() представима
как линейная комбинации своих аргументов:
представима
как линейная комбинации своих аргументов:
![]() ,
,
где ![]() - некоторые
константы, то соответствующая корреляционная зависимость называется линейной.
- некоторые
константы, то соответствующая корреляционная зависимость называется линейной.
Аналитическое задание корреляционной зависимости в виде
![]()
называется уравнением регрессии случайной величины ![]() на случайный вектор
на случайный вектор ![]() .
.
Двумерная корреляционная модель
Анализируется корреляционная
зависимость между двумя признаками ![]() ,
, ![]() .
.
Предполагается, что распределение вероятностей
двумерной случайной величины ![]() подчинено
закону Гаусса, т.е. плотность совместного распределения
подчинено
закону Гаусса, т.е. плотность совместного распределения ![]() ,
, ![]() определяется формулой:
определяется формулой:
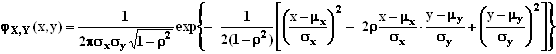
содержащей пять параметров:
![]() - математическое ожидание
- математическое ожидание ![]() ;
;
![]() - математическое ожидание
- математическое ожидание ![]() ;
;
![]() - дисперсия
- дисперсия ![]() ;
;
![]() - дисперсия
- дисперсия ![]() ;
;
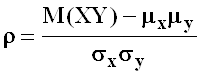 - коэффициент корреляции между
- коэффициент корреляции между ![]() ,
,
![]() .
.
Коэффициент корреляции как мера тесноты стохастической связи между двумя случайными величинами
Из условия нормальности совместного распределения
признаков ![]() ,
, ![]() непосредственно вытекает,
что распределение каждого их них также подчинено закону Гаусса с
соответствующими параметрами:
непосредственно вытекает,
что распределение каждого их них также подчинено закону Гаусса с
соответствующими параметрами:
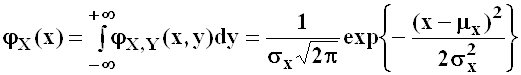 ;
;
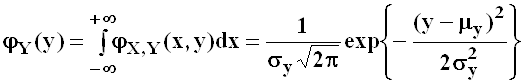 .
.
Если ![]() , то из
выражений, задающих двумерную и одномерные плотности распределения вероятностей
, то из
выражений, задающих двумерную и одномерные плотности распределения вероятностей
![]() ,
, ![]() ,
, ![]() следует, что
следует, что ![]() , т.е.
, т.е. ![]() ,
, ![]() есть независимые между
собой случайные величины.
есть независимые между
собой случайные величины.
Для случайных величин ![]() ,
, ![]() , совместное распределение
которых является нормальным, понятия "некоррелированность" и
"стохастическая независимость" эквивалентны.
, совместное распределение
которых является нормальным, понятия "некоррелированность" и
"стохастическая независимость" эквивалентны.
Таким образом, для решаемой задачи коэффициент
корреляции ![]() может служить мерой силы стохастической
взаимосвязи рассматриваемых случайных величин.
может служить мерой силы стохастической
взаимосвязи рассматриваемых случайных величин.
Вне рамок корреляционной модели равенство нулю коэффициента корреляции указывает лишь на некоррелированность исходных переменных, но не подтверждает отсутствие иной формы стохастической зависимости.
Коэффициент корреляции не имеет размерности и, следовательно, его можно использовать при анализе зависимости признаков, различающихся по мерным шкалам.
Значение ![]() по
абсолютной величине не превосходит единицы.
по
абсолютной величине не превосходит единицы.
Если ![]() ,
линейная связь между переменными
,
линейная связь между переменными ![]() и
и ![]() отсутствует.
отсутствует.
Значение ![]() указывает
на наличие функциональной линейной зависимости между ними.
указывает
на наличие функциональной линейной зависимости между ними.
По мере приближения ![]() к
единице условные дисперсии
к
единице условные дисперсии ![]() стремятся
к нулю, что свидетельствует о меньшем рассеянии значений переменных
стремятся
к нулю, что свидетельствует о меньшем рассеянии значений переменных ![]() ,
, ![]() относительно соответствующих
линий регрессии и о более тесной связи между данными переменными.
относительно соответствующих
линий регрессии и о более тесной связи между данными переменными.
Положительный знак коэффициента корреляции означает,
что прямые регрессии имеют в координатной плоскости ![]() положительный
тангенс угла наклона, с увеличением (или уменьшением) значения любой из
переменных
положительный
тангенс угла наклона, с увеличением (или уменьшением) значения любой из
переменных ![]() ,
, ![]() пропорционально в среднем
возрастает (соответственно убывает) значение другой переменной.
пропорционально в среднем
возрастает (соответственно убывает) значение другой переменной.
Отрицательный знак коэффициента корреляции указывает на обратную тенденцию.
Уравнения линейной парной регрессии
Функции регрессии ![]() на
на
![]() и
и ![]() на
на ![]() находятся с помощью
формул, определяющих условные математические ожидания:
находятся с помощью
формул, определяющих условные математические ожидания:
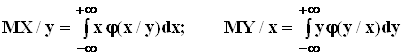 ,
,
При этом условные плотности распределения вероятностей случайных величин ![]() ,
, ![]() представляются в виде
отношений известных безусловных плотностей распределения:
представляются в виде
отношений известных безусловных плотностей распределения:
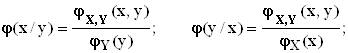
Дальнейшее интегрирование функций ![]() ,
,
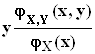 по x, соответственно по y, непосредственно дает уравнение регрессии
по x, соответственно по y, непосредственно дает уравнение регрессии ![]() на
на ![]() , а также уравнение
регрессии
, а также уравнение
регрессии ![]() на
на ![]() :
:
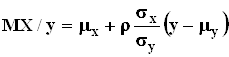 ;
;
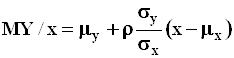 ,
,
![]() ;
; ![]() ,
,
где
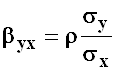 - коэффициент регрессии
- коэффициент регрессии ![]() на
на
![]() ;
;
 - коэффициент регрессии
- коэффициент регрессии ![]() на
на ![]() .
.
Линейный характер корреляционной зависимости между совместно нормально распределенными случайными величинами проявляется в том, что с изменением одной величины пропорционально изменяется условное математическое ожидание другой величины. Графики функций регрессии (именуемые линиями регрессии) представляют собой прямые.
В случае некоррелированности ![]() ,
, ![]() , т.е. при
, т.е. при ![]() , прямые регрессии
, прямые регрессии ![]() на
на ![]() и
и ![]() на
на ![]() параллельны соответственно
координатным осям
параллельны соответственно
координатным осям ![]() и
и ![]() .
.
Парный коэффициент детерминации
Степень рассеяния значений ![]() (или
(или
![]() ) относительно линии
регрессии
) относительно линии
регрессии ![]() на
на ![]() (или
(или ![]() на
на ![]() ) характеризуют (в среднем)
условные дисперсии:
) характеризуют (в среднем)
условные дисперсии:
![]()
Расчетные формулы для ![]() и
и
![]() находятся подобно тому,
как определялись функции регрессии
находятся подобно тому,
как определялись функции регрессии ![]() на
на ![]() и
и ![]() на
на ![]() .
.
В итоге,
![]() .
.
Квадрат коэффициента корреляции называется парным коэффициентом детерминации.
Из приведенных выражений для условных дисперсий
следует, что величина ![]() указывает долю
дисперсии одной случайной величины, обусловленную вариацией другой случайной
величины.
указывает долю
дисперсии одной случайной величины, обусловленную вариацией другой случайной
величины.
Эмпирические характеристики корреляционной зависимости
В практике статистических исследований параметры совместного распределения вероятностей случайных величин, включенных в анализ, как правило, неизвестны, и тесноту связи между переменными оценивают по статистическим данным и выборочным аналогам корреляционных характеристик.
С этой целью в двумерном корреляционном анализе используют "поле корреляции", строят корреляционную таблицу, рассчитывают точечные оценки параметров корреляционной модели, проверяют значимость параметров связи и находят интервальные оценки для значимых параметров, оценивают уравнения регрессии.
Корреляционное поле
Корреляционным полем называется совокупность нанесенных на координатную
плоскость ![]() реализаций случайного
вектора
реализаций случайного
вектора ![]() , т.е. выборочных точек
, т.е. выборочных точек ![]() .
.
По расположению точек корреляционного поля можно составить предварительное мнение о характерных особенностях зависимости случайных величин (например, о том, что значение какой-либо из этих величин в среднем возрастает или убывает при возрастании значения другой величины).
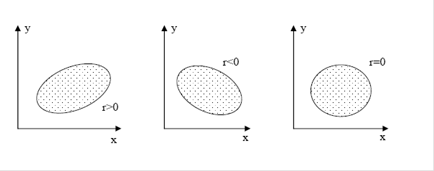
Наиболее точную информацию о направлении и силе связи между величинами ![]() ,
, ![]() дают коэффициент
корреляции и уравнения регрессии.
дают коэффициент
корреляции и уравнения регрессии.
Корреляционная таблица
В понятийном смысле - представляет собой обобщение понятия «вариационный
ряд», с прикладной точки зрения - является формой компактной записи выборочных
данных ![]() двумерной случайной
величины
двумерной случайной
величины ![]() :
:
|
|
|
|
… |
|
… |
|
|
|
|
|
|
… …
…
… |
|
… …
…
… |
|
|
|
|
|
|
… |
|
… |
|
n |
где
![]() ;
; ![]()
- упорядоченные по возрастанию последовательности всех
различных значений ![]() , соответственно
, соответственно ![]() , имеющихся в выборке
, имеющихся в выборке ![]() .
.
![]() - количество пар
- количество пар ![]() .
.
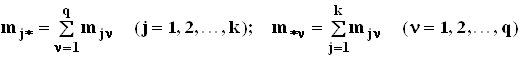 - сумма элементов
- сумма элементов ![]() -го
столбца, соответственно -
-го
столбца, соответственно - ![]() -ой
строки корреляционной таблицы. При этом
-ой
строки корреляционной таблицы. При этом
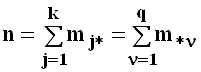 .
.
Точечные оценки параметров двумерного распределения
Для получения приближенных значений параметров корреляционной модели используют, как правило, метод моментов, расчеты производят согласно следующим формулам.
|
Характеристики
распределения случайного вектора |
||
|
теоретические |
оценки
по выборочным данным |
|
|
сгруппированным |
не сгруппированным |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Приведенные эмпирические характеристики двумерного
нормального закона распределения случайного вектора ![]() обладают свойством
состоятельности,
обладают свойством
состоятельности, ![]() ,
, ![]() являются, кроме того, несмещенными
и эффективными оценками.
являются, кроме того, несмещенными
и эффективными оценками.
Аппроксимация уравнений регрессии
![]() ;
; ![]() .
.
Проверка гипотезы об отсутствии корреляционной зависимости между случайными величинами
Выборочный парный коэффициент корреляции r, найденный по конечному числу статистических данных, практически всегда отличен от нуля, однако, отсюда не всегда следует, что неизвестный генеральный парный коэффициент корреляции ρ также не равен нулю, т.е. что корреляционная зависимость действительно имеет место. Требуется дополнительно осуществить проверку предположения о значимости коэффициента корреляции.
При справедливости основной гипотезы ![]() ("корреляционная
зависимость между
("корреляционная
зависимость между ![]() ,
, ![]() отсутствует") статистика
применяемого критерия
отсутствует") статистика
применяемого критерия

имеет распределение
Стьюдента с числом степеней свободы, равным ![]() .
.
При уровне значимости ![]() гипотеза
гипотеза ![]() отвергается, если
выполняется неравенство
отвергается, если
выполняется неравенство ![]() , в
котором под символом
, в
котором под символом ![]() понимается
критическое значение, удовлетворяющее уравнению
понимается
критическое значение, удовлетворяющее уравнению
![]() .
.
При отвержении основной
гипотезы заключают, что признаки ![]() ,
, ![]() связаны линейным
корреляционным соотношением, в ином случае делают вывод, что на основе имеющейся
выборки корреляционная зависимость между ними не установлена.
связаны линейным
корреляционным соотношением, в ином случае делают вывод, что на основе имеющейся
выборки корреляционная зависимость между ними не установлена.
Если в результате
проверки гипотеза ![]() будет
отвергнута, то полагают, что коэффициент корреляции
будет
отвергнута, то полагают, что коэффициент корреляции ![]() значимо
(существенно) отличается от нуля, а рассчитанное по статистическим данным
значение r может быть использовано в качестве его точечной
оценки.
значимо
(существенно) отличается от нуля, а рассчитанное по статистическим данным
значение r может быть использовано в качестве его точечной
оценки.
Интервальная оценка коэффициента корреляции
корреляционная регрессия уравнение математический
При построении доверительного интервала для
неизвестного коэффициента корреляции ![]() используется
специальная функция -
используется
специальная функция - ![]() -преобразование
Фишера (гиперболический арктангенс) выборочного коэффициента корреляции r:
-преобразование
Фишера (гиперболический арктангенс) выборочного коэффициента корреляции r:
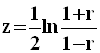 .
.
![]() - возрастающая нечетная функция: z(-r) = -z(r).
- возрастающая нечетная функция: z(-r) = -z(r).
Распределение вероятностей значений ![]() приближается
(тем более точно, чем больше объем выборки n) нормальным
распределением вероятностей
приближается
(тем более точно, чем больше объем выборки n) нормальным
распределением вероятностей ![]() с параметрами:
с параметрами:
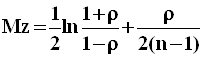 и
и 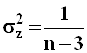 .
.
Статистика 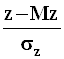 имеет асимптотическое
стандартное нормальное распределение
имеет асимптотическое
стандартное нормальное распределение ![]() .
.
Асимптотически точный
доверительный интервал надежности ![]() для
нормированного отклонения z:
для
нормированного отклонения z:
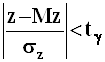 ,
,
где ![]() - квантиль уровня
- квантиль уровня ![]() распределения
распределения ![]() , т.е. корень уравнения
, т.е. корень уравнения ![]() .
.
Доверительный интервал
для математического ожидания ![]() :
:
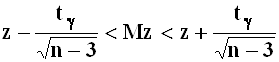 .
.
Величиной 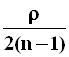 в выражении
в выражении ![]() можно пренебречь, принимая
во внимание, что она при
можно пренебречь, принимая
во внимание, что она при ![]() есть
бесконечно малая более высокого порядка в сравнении с
есть
бесконечно малая более высокого порядка в сравнении с 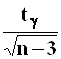 .
.
Доверительный интервал
для гиперболического арктангенса коэффициента корреляции ![]() :
:
 .
.
Решение относительно ![]() данного двойного
неравенства приводит к искомому доверительному интервалу для коэффициента
корреляции:
данного двойного
неравенства приводит к искомому доверительному интервалу для коэффициента
корреляции:
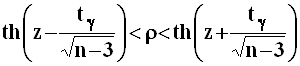 ,
,
с границами,
определяемыми как значения гиперболического тангенса  для значений
для значений ![]() , равных соответственно
, равных соответственно  и
и  .
.
Функция ![]() задает преобразование,
обратное
задает преобразование,
обратное ![]() -преобразованию Фишера.
Следовательно,
-преобразованию Фишера.
Следовательно, ![]() .
.
Этапы определения ДИ для коэффициента корреляции
- находится выборочный коэффициент корреляции r;
-
выполняется прямое преобразование
Фишера значения r: ![]() ;
;
-
выбирается квантиль ![]() , исходя из условия
, исходя из условия ![]() ;
;
-
вычисляются значения  и
и 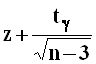 ;
;
- с помощью обратного преобразования Фишера находятся границы ДИ:
 и
и  .
.
Доверительные интервалы для коэффициентов регрессии
Их построение осуществляется в соответствии с общей схемой. При этом используются статистики:
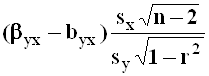 ;
; 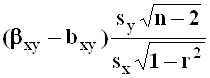 ,
,
имеющие распределение Стьюдента с числом степеней
свободы, равном ![]() .
.
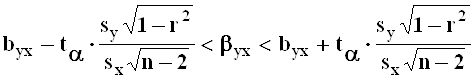 ;
;
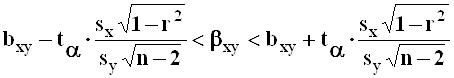 ,
,
где ![]() - корень уравнения
- корень уравнения ![]() .
.
Многомерная корреляционная модель
Предполагается, что совместное распределение
анализируемых случайных переменных (признаков) ![]() подчинено
h-мерному нормальному закону.
подчинено
h-мерному нормальному закону.
Типовые задачи
¨ определение тесноты связи между некоторыми переменными при фиксировании или исключении влияния остальных переменных;
¨ определение тесноты связи одной из рассматриваемых переменных с совокупностью всех остальных переменных, включенных в анализ.
Корреляционная матрица
Начальный этап многомерного корреляционного анализа количественных признаков состоит в оценке (приближении) на основе выборочных данных матрицы
 ,
,
элементы которой 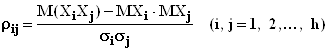 - парные коэффициенты
корреляции переменных
- парные коэффициенты
корреляции переменных ![]() .
.
Выборочная корреляционная матрица
В качестве статистического аналога корреляционной
матрицы ![]() принимается матрица
принимается матрица
 ,
,
здесь 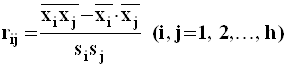 - выборочные парные
коэффициенты корреляции переменных
- выборочные парные
коэффициенты корреляции переменных ![]() .
.
Свойство корреляционных матриц
Матрицы ![]() , qh симметричны
относительно главной диагонали.
, qh симметричны
относительно главной диагонали.
Вся имеющаяся для
анализа статистическая информация о зависимостях между случайными величинами ![]() содержится в выборочной
корреляционной матрице
содержится в выборочной
корреляционной матрице ![]() .
.
Однако раскрытие
многообразия взаимосвязей данных переменных непосредственно по их парным
коэффициентам корреляции невозможно. Для проведения исследования при решении
указанных типовых задач необходимо вычислять также частные и множественные
коэффициенты корреляции, представляющие собой определенные действительные
функции матрицы ![]() .
.
Частный коэффициент корреляции
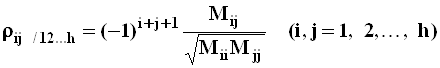 ,
,
где ![]() - минор
элемента
- минор
элемента ![]() матрицы
матрицы ![]() , т.е. определитель
матрицы, получающейся из корреляционной матрицы удалением
, т.е. определитель
матрицы, получающейся из корреляционной матрицы удалением ![]() -ой строки и
-ой строки и ![]() -го столбца.
-го столбца.
Свойства частного коэффициента корреляции
![]() обладает всеми свойствами парного коэффициента корреляции
обладает всеми свойствами парного коэффициента корреляции ![]() , т.к. является
коэффициентом корреляции
, т.к. является
коэффициентом корреляции ![]() для их
условного двумерного распределения. В отличие от парного коэффициента
корреляции
для их
условного двумерного распределения. В отличие от парного коэффициента
корреляции ![]() , на величине которого
сказывается не только влияние переменных
, на величине которого
сказывается не только влияние переменных ![]() друг
на друга, но и воздействие остальных
друг
на друга, но и воздействие остальных ![]() переменных,
частный коэффициент корреляции
переменных,
частный коэффициент корреляции ![]() позволяет
характеризовать тесноту связи между признаками
позволяет
характеризовать тесноту связи между признаками ![]() в
«чистом» виде, исключая при анализе зависимости влияние других переменных. Если
парный коэффициент корреляции
в
«чистом» виде, исключая при анализе зависимости влияние других переменных. Если
парный коэффициент корреляции ![]() больше
соответствующего частного коэффициента
больше
соответствующего частного коэффициента ![]() ,
то можно заключить, что остальные рассматриваемые переменные усиливают
взаимосвязь между изучаемыми величинами
,
то можно заключить, что остальные рассматриваемые переменные усиливают
взаимосвязь между изучаемыми величинами ![]() .
Уменьшение значения парного коэффициента корреляции, в сравнении с отвечающим
ему частным коэффициентом корреляции, свидетельствует об ослаблении связи между
исследуемыми величинами
.
Уменьшение значения парного коэффициента корреляции, в сравнении с отвечающим
ему частным коэффициентом корреляции, свидетельствует об ослаблении связи между
исследуемыми величинами ![]() в
результате воздействия других переменных.
в
результате воздействия других переменных.
Выборочный частный коэффициент корреляции
Точечная оценка ![]() определяется
по формуле:
определяется
по формуле:
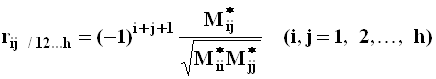 ,
,
здесь ![]() - минор элемента
- минор элемента ![]() выборочной корреляционной
матрицы
выборочной корреляционной
матрицы ![]() .
.
В случае трехмерной корреляционной модели для
переменных ![]() находятся три частных
коэффициента корреляции:
находятся три частных
коэффициента корреляции:
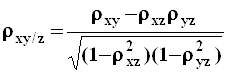 ;
;
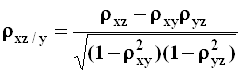 ;
;
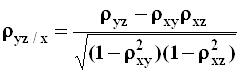 .
.
![]() называется частным коэффициентом детерминации.
называется частным коэффициентом детерминации.
Величина ![]() есть
доля дисперсии переменной
есть
доля дисперсии переменной ![]() ,
обусловленная вариацией
,
обусловленная вариацией ![]() при
фиксированных остальных рассматриваемых переменных.
при
фиксированных остальных рассматриваемых переменных.
Множественный коэффициент корреляции
Мерой тесноты линейной взаимосвязи между переменной ![]() и совокупностью остальных
переменных
и совокупностью остальных
переменных ![]() служит множественный
коэффициент корреляции:
служит множественный
коэффициент корреляции:
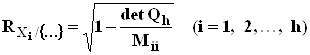 ,
,
Где
![]() - определитель матрицы
- определитель матрицы ![]() ;
;
![]() - минор
- минор ![]() -го элемента
главной диагонали матрицы
-го элемента
главной диагонали матрицы ![]() .
.
Если ![]() , то
множественный коэффициент корреляции
, то
множественный коэффициент корреляции ![]() совпадает
с абсолютным значением парного коэффициента корреляции
совпадает
с абсолютным значением парного коэффициента корреляции ![]() , т.е.
, т.е. ![]() есть обобщение
есть обобщение ![]() .
.
По величине множественного коэффициента корреляции делается вывод о тесноте, но не о направлении взаимосвязи.
Свойства множественного коэффициента корреляции
- Численное значение множественного коэффициента корреляции заключено между нулем и единицей:
![]() .
.
-
Если ![]() ,
то переменная
,
то переменная ![]() связана с
остальными рассматриваемыми случайными величинами
связана с
остальными рассматриваемыми случайными величинами ![]() линейной
функциональной зависимостью.
линейной
функциональной зависимостью.
Например, для трехмерной корреляционной модели, если ![]() , то точки
, то точки ![]() расположены в плоскости
регрессии
расположены в плоскости
регрессии ![]() на
на ![]() .
.
-
Если ![]() ,
то случайная величина
,
то случайная величина ![]() стохастически
независима от других переменных, входящих в анализ.
стохастически
независима от других переменных, входящих в анализ.
В частности, если ![]() ,
то одномерная случайная величина
,
то одномерная случайная величина ![]() и
двумерная случайная величина
и
двумерная случайная величина ![]() являются
независимыми (в силу нормальности их совместного распределения).
являются
независимыми (в силу нормальности их совместного распределения).
- Множественный коэффициент корреляции не уменьшается при введении в модель дополнительных признаков и не увеличивается при исключении отдельных признаков из модели.
-
По величине множественный
коэффициент корреляции переменной ![]() не
меньше абсолютной величины частного коэффициента корреляции данной и любой
другой переменной
не
меньше абсолютной величины частного коэффициента корреляции данной и любой
другой переменной ![]() :
:
![]() .
.
Выборочный множественный коэффициент корреляции
В качестве точечной оценки ![]() принимается
принимается
![]() .
.
где ![]() - минор
- минор ![]() -го элемента главной
диагонали выборочной корреляционной матрицы
-го элемента главной
диагонали выборочной корреляционной матрицы ![]() .
.
В случае трехмерной корреляционной модели для
переменных ![]() вычисляются три
множественных коэффициента корреляции:
вычисляются три
множественных коэффициента корреляции:
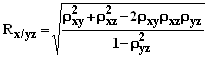 ;
;
 ;
;
 .
.
![]() называется множественным коэффициентом детерминации.
называется множественным коэффициентом детерминации.
Множественный коэффициент детерминации ![]() показывает долю дисперсии
исследуемой случайной величины
показывает долю дисперсии
исследуемой случайной величины ![]() ,
обусловленную изменением остальных переменных
,
обусловленную изменением остальных переменных ![]() .
.
Уравнения регрессии для трехмерной корреляционной модели
I.
При фиксировании значения
одной случайной величины в системе случайных величин ![]() трехмерное нормальное
распределение данных величин становится условным двумерным нормальным
распределением, определяемым пятью параметрами.
трехмерное нормальное
распределение данных величин становится условным двумерным нормальным
распределением, определяемым пятью параметрами.
Если фиксировано, например, значение ![]() случайной величины
случайной величины ![]() , то условное двумерное
нормальное распределение
, то условное двумерное
нормальное распределение ![]() характеризуется
следующими параметрами:
характеризуется
следующими параметрами:
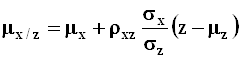 ;
; 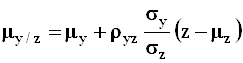 ;
;
![]() ;
; ![]() ;
;
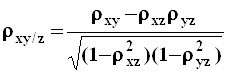 .
.
Линейная корреляционная зависимость между величинами ![]() при фиксированном значении
при фиксированном значении
![]() случайной величины
случайной величины ![]() графически выражается
прямыми регрессии в плоскости
графически выражается
прямыми регрессии в плоскости ![]() :
:
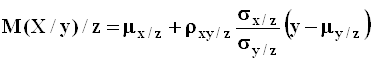 ;
;
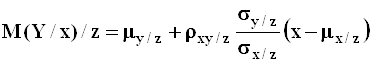 .
.
II.
При фиксированных значениях
двух переменных в системе случайных величин ![]() трехмерное
нормальное распределение есть определяемое двумя параметрами условное
одномерное нормальное распределение соответствующей переменной.
трехмерное
нормальное распределение есть определяемое двумя параметрами условное
одномерное нормальное распределение соответствующей переменной.
В частности, при фиксированных значениях ![]() компонент двумерного
случайного вектора
компонент двумерного
случайного вектора ![]() совместное
распределение переменных
совместное
распределение переменных ![]() становится
условным одномерным нормальным распределением случайной величины
становится
условным одномерным нормальным распределением случайной величины ![]() , параметрами которого
являются условное математическое ожидание
, параметрами которого
являются условное математическое ожидание
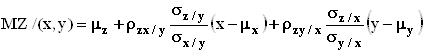
и условная дисперсия ![]() ,
совпадающая с
,
совпадающая с ![]() - остаточной
дисперсией относительно плоскости регрессии
- остаточной
дисперсией относительно плоскости регрессии ![]() на
на
![]() :
:
![]() .
.
Уравнение регрессии ![]() на
на ![]() может быть представлено в
виде:
может быть представлено в
виде:
![]() ,
,
где 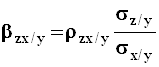 ;
; 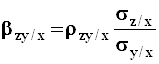 - частные коэффициенты
регрессии.
- частные коэффициенты
регрессии.
Для расчета условных средних квадратических отклонений используются формулы:
![]() ;
; ![]() ;
;
![]() ;
; ![]() .
.
Функция регрессии линейно зависит от двух переменных ![]() . Соответствующая ей
поверхность представляет собой плоскость.
. Соответствующая ей
поверхность представляет собой плоскость.
Для рассматриваемой модели имеют место три уравнения регрессии и три отвечающие им плоскости регрессии.
Необходимые для расчетов коэффициентов уравнений регрессии
оценки девяти определяющих совместное распределение ![]() параметров
трехмерной корреляционной модели по выборочным данным
параметров
трехмерной корреляционной модели по выборочным данным ![]() осуществляются по
формулам:
осуществляются по
формулам:
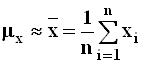 ;
; ![]() ;
; 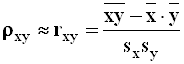 ;
;
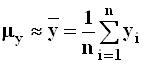 ;
; ![]() ;
; 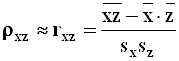 ;
;
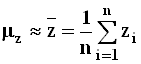 ;
; ![]() ;
; 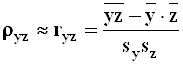 .
.
Проверка значимости коэффициентов связи
а) для частного коэффициента корреляции
Если верна основная гипотеза ![]() , то статистика
, то статистика
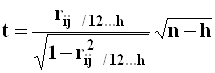
имеет распределение
Стьюдента с числом степеней свободы, равным ![]() .
.
При уровне значимости ![]() исходная
гипотеза отвергается, если справедливо неравенство
исходная
гипотеза отвергается, если справедливо неравенство ![]() ,
где
,
где ![]() - критическое значение,
удовлетворяющее условию
- критическое значение,
удовлетворяющее условию ![]() .
.
б) для множественного коэффициента корреляции
При справедливости основной гипотезы ![]() статистика
статистика
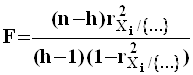
имеет распределение
Фишера-Снедекора с ![]() и
и ![]() степенями свободы.
степенями свободы.
При уровне значимости ![]() гипотеза отвергается, если
выполняется неравенство
гипотеза отвергается, если
выполняется неравенство ![]() , где
, где ![]() - критическое значение,
удовлетворяющее условию
- критическое значение,
удовлетворяющее условию ![]() .
.
Интервальная оценка частных коэффициентов корреляции
- выполняется прямое преобразование Фишера значения
![]() :
: 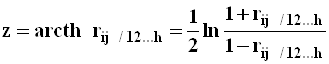 ;
;
-
выбирается квантиль ![]() , исходя из условия
, исходя из условия ![]() ;
;
-
вычисляются значения  и
и  ;
;
- с помощью обратного преобразования Фишера находятся границы ДИ:
 и
и  .
.