Реферат: Застосування частинних похідних

ЗАСТОСУВАННЯ ЧАСТИННИХ ПОХІДНИХ

1. Дотична площина та нормаль до поверхні. Геометричний зміст диференціала функції двох змінних

Нехай задано поверхню

. (1)

Точка належить цій поверхні і функція диференційована в точці , причому не всі частинні похідні в точці дорівнюють нулю, тобто

Розглянемо довільну криву, яка проходить через точку , лежить на поверхні (1) і задається рівнянням

де точці відповідає параметр .

Оскільки крива лежить на поверхні, то координати її точок задовольняють рівняння (1):

. (2)

Диференціюючи рівність (2), маємо:

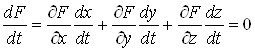. (3)

Ця рівність показує, що вектори (рис. 1)

ортогональні, причому другий з них є напрямним вектором дотичної до кривої у точці .

Крім того, з рівності (3) випливає, що дотичні до всіх кривих, які проходять через точку і лежать на поверхні (1), ортогональні до одного й того самого вектора . Тоді всі ці дотичні лежать в одній і тій самій площині, яка називається дотичною площиною до поверхні в точці .

Знайдемо рівняння дотичної площини. Оскільки ця площина проходить через точку перпендикулярно до вектора , то її рівняння має вигляд.

.(4)

Нормаллю до поверхні в точці називають пряму, що проходить через точку перпендикулярно до дотичної площини в цій точці.

Оскільки нормаль проходить через точку і має напрямний вектор , то канонічні рівняння нормалі мають такий вигляд:

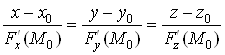. (5)

Якщо рівняння поверхні задано в явній формі, то, поклавши, отримаємо

тоді рівняння (4) і (5) наберуть вигляду:

;(6)

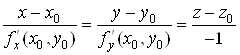.(7)

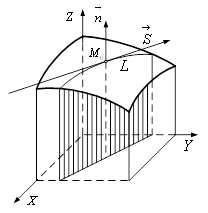
Рисунок 1 – Дотична площина та нормаль до поверхні

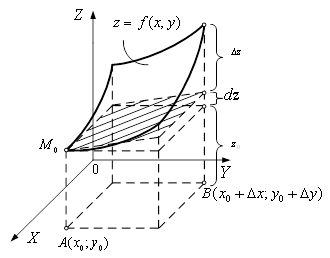
Рисунок 2 – Геометричний зміст повного диференціала функції

З'ясуємо геометричний зміст повного диференціала функції. Якщо у формулі (6) покласти, то ця формула запишеться у вигляді

Права частина цієї рівності є повним диференціалом функції в точці, тому .

Таким чином, повний диференціал функції двох змінних у точці дорівнює приросту аплікати точки на дотичній площині до поверхні в точці, якщо від точки перейти до точки (рис. 2).

Зауваження 1. Ми розглянули випадок, коли функція диференційована в точці і.

Якщо ці умови не виконуються в деякій точці (її називають особливою), то дотична та нормаль в такій точці можуть не існувати.

Зауваження 2. Якщо поверхня (1) є поверхнею рівня для деякої функції, тобто, то вектор

буде напрямним вектором нормалі до цієї поверхні рівня.

2. Скалярне поле. Похідна за напрямом. Градієнт

Область простору, кожній точці якої поставлено у відповідність значення деякої скалярної величини , називають скалярним полем. Інакше кажучи, скалярне поле – це скалярна функція разом з областю її визначення.

Рисунок 3.3 – Вектор

Прикладами скалярних полів є поле температури даного тіла, поле густини даного неоднорідного середовища, поле вологості повітря, поле атмосферного тиску, поле потенціалів заданого електростатичного поля тощо.

Для того щоб задати скалярне поле, достатньо задати скалярну функцію точки і область її визначення.

Якщо функція не залежить від часу, то скалярне поле називають стаціонарним, а скалярне поле, яке змінюється з часом, – нестаціонарним. Надалі розглядатимемо лише стаціонарні поля.

Якщо в просторі ввести прямокутну систему координат, то точка в цій системі матиме певні координати і скалярне поле u стане функцією цих координат:

Якщо скалярна функція залежить тільки від двох змінних, наприклад x і , то відповідне скалярне поле називають плоским; якщо ж функція залежить від трьох змінних: x, і, то скалярне поле називають просторовим.

Геометрично плоскі скалярні поля зображують за допомогою ліній рівня, а просторові – за допомогою поверхонь рівня.

Для характеристики швидкості зміни поля в заданому напрямі введемо поняття похідної за напрямом.

Нехай задано скалярне поле . Візьмемо в ньому точку і проведемо з цієї точки вектор, напрямні косинуси якого .

На векторі на відстані від його початку візьмемо точку .

Тоді

Обчислимо тепер приріст функції при переході від точки до точки у напрямі вектора:

Якщо існує границя відношення при, то цю границю називають похідною функції в точці за напрямом вектора і позначають, тобто

Виведемо формулу для обчислення похідної за напрямом. Припустимо, що функція диференційована в точці M. Тоді її повний приріст у цій точці можна записати так:

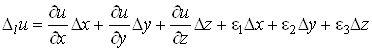де – нескінченно малі функції при.

Оскільки

то

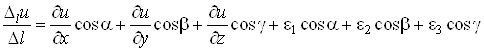Перейшовши до границі при, отримаємо формулу для обчислення похідної за напрямом

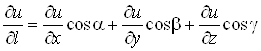.(8)

З формули (З.8) випливає, що частинні похідні є окремими випадками похідної за напрямом. Дійсно, якщо збігається з одним із ортів, або , то похідна за напрямом збігається з відповідною частинною похідною. Наприклад, якщо, то, тому

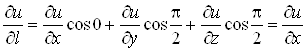Подібно до того як частинні похідні характеризують швидкість зміни функції в напрямі осей координат, так і похідна показує швидкість зміни скалярного поля в точці за напрямом вектора.

Абсолютна величина похідної відповідає значенню швидкості, а знак похідної визначає характер зміни функції в напрямі (зростання чи спадання).

Очевидно, що похідна за напрямом, який протилежний напряму, дорівнює похідній за напрямом, взятій з протилежним знаком.

Справді, при зміні напряму на протилежний кути зміняться на , тому

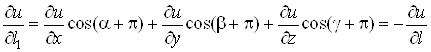Фізичний зміст цього результату такий: зміна напряму на протилежний не впливає на значення швидкості зміни поля, а тільки на характер зміни поля. Якщо, наприклад, в напрямі поле зростає, то в напрямі воно спадає, і навпаки.

Якщо поле плоске, тобто задається функцією то напрям вектора цілком визначається кутом 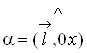. Тому, поклавши у формулі (8) та, отримаємо

Вектор, координатами якого є значення частинних похідних функції в точці називають градієнтом функції в цій точці і позначають. Отже,

. (9)

Зв'язок між градієнтом і похідною в даній точці за довільним напрямом показує така теорема.

Теорема. Похідна функції у точці за напрямом вектора дорівнює проекції градієнта функції в цій точці на вектор, тобто

.(10)

Доведення

Нехай – кут між градієнтом (9) і одиничним вектором (рис. 4), тоді з властивостей скалярного добутку [1] отримаємо

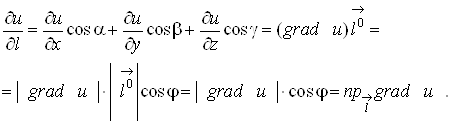
Зазначимо деякі властивості градієнта.

1. Похідна в даній точці за напрямом вектора має найбільше

значення, якщо напрям вектора збігається з напрямом градієнта, причому

.(11)

Справді, з формули (10) випливає, що похідна за напрямом досягає максимального значення (11), якщо , тобто якщо напрям вектора збігається з напрямом градієнта.

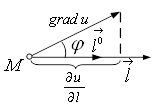
Рисунок 4 – Зв'язок між градієнтом і похідною за напрямом

Таким чином, швидкість зростання скалярного поля в довільній точці є максимальною у напрямі градієнта. Зрозуміло, що у напрямі, протилежному до напряму градієнта, поле найшвидше зменшуватиметься.

2. Похідна за напрямом вектора, перпендикулярного до градієнта, дорівнює нулю. Інакше кажучи, швидкість зміни поля у напрямі, перпендикулярному до градієнта, дорівнює нулю, тобто скалярне поле залишається сталим.

Справді, за формулою (10), якщо.

Вектор-градієнт у кожній точці поля перпендикулярний до поверхні рівня, яка проходить через цю точку. Це твердження випливає з того, що напрямний вектор нормалі до поверхні рівня, яка проходить через точку має координати (п. 1)

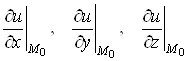4. Справедливі рівності:

Доведення

Доведемо, наприклад, третю рівність. Маємо:

Решта рівностей доводяться аналогічно.

3. Формула Тейлора для функції двох змінних

Якщо функція однієї змінної має на відрізку неперервні похідні до -го порядку включно, то справджується формула Тейлора:

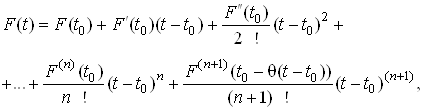(12)

Нехай ,

тоді, тому формулу (12) можна записати у вигляді

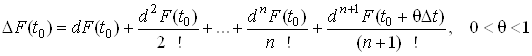.(13)

В аналогічному вигляді формулу Тейлора можна отримати і для функції багатьох змінних. Розглянемо функцію двох змінних.

Нехай функція в області має неперервні частинні похідні до -го порядку включно. Візьмемо дві точки та такі, щоб відрізок належав області.

Введемо нову змінну :

, , .(14)

При за цими формулами отримаємо координати точки , а при – координати точки . Якщо змінюватиметься на відрізку , то точка опише весь відрізок . Тоді вздовж цього відрізка функція буде функцією однієї змінної :

.(15)

Запишемо формулу (13) для функції (15) при:

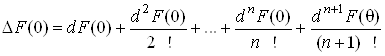.(16)

Обчислимо диференціали, що входять у формулу (16). З рівностей (14) і (15) маємо

Оскільки, то

.(17)

Аналогічно

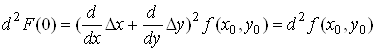.(18)

Продовжуючи цей процес, знайдемо

. (19)

Крім того приріст

.(20)

Підставивши вирази (17 – 20) у формулу (14), отримаємо

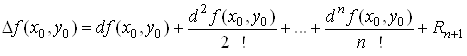,(21)

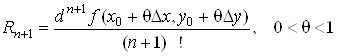.(22)

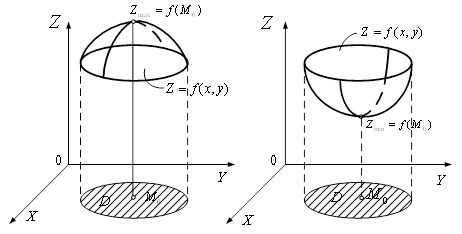
Рисунок 5 – Локальний максимум (мінімум) функції

Формулу (21) називають формулою Тейлора для функції двох змінних з залишковим членом у форму Лагранжа. Цю формулу використовують для наближених обчислень. Для різних значень n з формули (21) можна отримати рівності для наближеного обчислення значень функції. Абсолютну похибку цих наближених рівностей оцінюють через залишковий член (22).

Формула Тейлора (21) для функції двох змінних нагадує формулу Тейлора (13) для функції однієї змінної. Але насправді, якщо розкрити вирази для диференціалів у формулі (21), то отримаємо складнішу формулу, ніж для

функції однієї змінної. Наприклад, при формула (21) має вигляд:

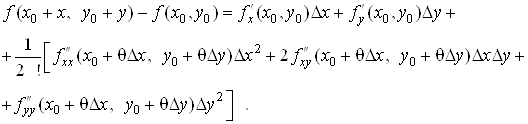(23)

4. Локальні екстремуми функції двох змінних

Нехай функція визначена в області, а точка. Якщо існує окіл точки , який належить області і для всіх відмінних від точок цього околу виконується нерівність, то точку називають точкою локального максимуму (мінімуму) функції, а число – локальним максимумом (мінімумом) цієї функції (рис. 5). Точки максимуму та мінімуму функції називають її точками екстремуму.

Це означення можна перефразувати так. Покладемо , тоді

Якщо приріст функції при всіх достатньо малих за абсолютною величиною приростах і , то функція в точці досягає локального максимуму (локального мінімуму). Інакше кажучи, в околі екстремальної точки прирости функції мають один і той самий знак.

Теорема 1 (необхідні умови екстремуму). Якщо функція має в точці локальний екстремум, то в цій точці частинні похідні першого порядку за змінними x та дорівнюють нулю або не існують.

Доведення

Нехай – точка екстремуму. Тоді функція буде функцією однієї змінної. Ця функція має екстремум у точці ц, тому її похідна дорівнює нулю або не існує.

Аналогічно, розглянувши функцію отримаємо, що

дорівнює нулю або не існує.

Подібна теорема справедлива для функції n змінних. Точку, в якій частинні похідні першого порядку функції дорівнюють нулю, тобто, називають стаціонарною точкою функції.

Стаціонарні точки та точки, в яких частинні похідні не існують, називаються критичними точками.

Таким чином, якщо функція в будь-якій точці досягає екстремуму, то це може статися лише в критичній точці. Проте не всяка критична точка є точкою екстремуму, тобто теорема 1 встановлює лише необхідні, але не достатні умови екстремуму. Наприклад, частинні похідні функції дорівнюють нулю в точці. Але ця функція у вказаній точці екстремуму не має, тому що в досить малому околі точки вона набуває як додатних (при), так і від'ємних (при) значень.

Слід зазначити, що в задачах з практичним змістом, як правило, відомо, що функція має екстремум. Якщо така функція має лише одну критичну точку, то ця точка і буде точкою екстремуму.

Теорема 2 (достатні умови екстремуму). Нехай у стаціонарній точці і деякому її околі функція має неперервні частинні похідні другого порядку. Якщо

то функція має в точці екстремум, причому максимум при і мінімум при . Якщо , то в точці функція екстремуму не має.

Доведення

Запишемо формулу Тейлора (23) для функції в околі стаціонарної точки. Враховуючи, що, отримаємо:

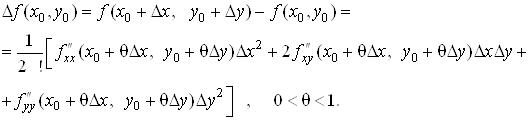
У випадку мінімуму для довільних достатньо малих значень та права частина цієї рівності має бути додатною, а у випадку максимуму – від'ємною.

Внаслідок неперервності других частинних похідних для цього достатньо, щоб диференціал другого порядку в точці

зберігав знак для малих значень та.

Введемо такі позначення, , , тоді

Нехай – кут між відрізком , де – точка з координатами і віссю; тоді., тому при маємо

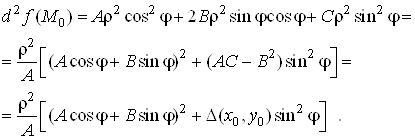
Розглянемо тепер п’ять можливих випадків.

1. Нехай і, тоді , тому при досить малих значеннях приріст, тобто функція має в точці максимум.

2. Аналогічно доводимо, що коли і, то функція має в точці мінімум.

Нехай і. Якщо з точки рухатися вздовж променя

, то. Якщо взяти таким, щоб або , то

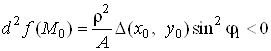Отже, при малих значеннях приріст в околі точки не зберігає знак, тому ця точка не є точкою екстремуму функції.

4. Аналогічно встановлюємо, що коли і, то функція в точці також не має екстремуму.

5. Нехай і, тоді і

При досить малих кутах знак величини збігається зі знаком , тому знак величини залежатиме від знака множника. Але знак величини змінюється при і, бо . Отже, в достатньо малому околі точки знак не збігається, тобто функція в цій точці екстремуму не має.

Зауваження. З доведення теореми 2 випливають так звані другі достатні умови екстремуму: функція має мінімум у стаціонарній точці, якщо диференціал другого порядку в цій точці , і максимум – якщо .

Можна довести, що другі достатні умови екстремуму справедливі для функцій довільного числа змінних.

На основі теорем 1 і 2 отримаємо правило дослідження диференційовних функцій двох змінних на екстремум. Щоб знайти екстремум диференційовної функції, необхідно:

1) знайти стаціонарні точки функції із системи рівнянь:

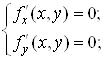
2) у кожній стаціонарній точці обчислити вираз

;

якщо , то – точка екстремуму функції, причому точка максимуму при і мінімуму при; якщо, то точка не є точкою екстремуму функції;

3) обчислити значення функції у точках максимуму та мінімуму.

Якщо, то ніякого висновку про характер стаціонарної точки зробити не можна і потрібне додаткове дослідження.

5. Найбільше та найменше значення функції

диференціал функція дотична нормаль екстремум

Відомо, що функція, задана і неперервна в замкненій та обмеженій області, досягає в цій області найбільшого і найменшого значень. У внутрішніх точках області диференційовна функція може набувати цих значень лише в точках локального екстремуму. Тому потрібно знайти всі стаціонарні точки функції, які належать області, розв'язавши систему рівнянь, і обчислити значення функції в цих точках. Потім потрібно дослідити функцію на екстремум на межі області. Використовуючи рівняння межі, цю задачу зводять до знаходження абсолютного екстремуму функції однієї змінної [8]. Серед здобутих таким чином значень функції всередині і на межі області вибирають найбільше і найменше значення.

Зазначимо, що загального методу знаходження найбільшого та найменшого значень для довільної неперервної функції в замкненій та обмеженій області немає.