
Рефераты по рекламе
Рефераты по философии
Рефераты по финансам
Рефераты по химии
Рефераты по цифровым устройствам
Рефераты по экологическому праву
Рефераты по экономико-математическому моделированию
Рефераты по экономической географии
Рефераты по экономической теории
Рефераты по этике
Рефераты по юриспруденции
Рефераты по языковедению
Рефераты по юридическим наукам
Рефераты по истории
Рефераты по компьютерным наукам
Рефераты по медицинским наукам
Рефераты по финансовым наукам
Рефераты по управленческим наукам
Рефераты по строительным наукам
Психология педагогика
Промышленность производство
Биология и химия
Языкознание филология
Издательское дело и полиграфия
Рефераты по краеведению и этнографии
Рефераты по религии и мифологии
Рефераты по медицине
Рефераты по сексологии
Рефераты по москвоведению
Рефераты по экологии
Краткое содержание произведений
Рефераты по физкультуре и спорту
Топики по английскому языку
Рефераты по математике
Рефераты по музыке
Остальные рефераты
Курсовая работа: Інтерполювання функцій
Курсовая работа: Інтерполювання функцій
Зміст
Вступ
Розділ I
Інтерполювання функцій
1.1 Постановка задачі
1.2 Інтерполяційні формули Ньютона
1.2.1 Перша інтерполяційна формула Ньютона
1.2.2 Друга інтерполяційна формула Ньютона
1.2.3 Оцінка похибок інтерполяційних формул Ньютона
1.3 Інтерполяційні формули Гауса
1.4 Інтерполяційна формула Бесселя
1.5 Інтерполяційна формула Стірлінга
1.6 Оцінки похибок центральних інтерполяційних формул
1.7 Інтерполяційна формула Ньютона для нерівновіддалених вузлів
1.8 Приклади застосування інтерполяційних формул
1.8.1 Приклад 1
1.8.2 Приклад 2
1.9 Програмна реалізація
1.9.1 Призначення програми
1.9.2 Основні процедури
1.9.3 Інструкція по використанню програми
1.9.4 Перевірка працездатності програми
Розділ ІІ
Література
Додатки
У зв’язку з розвитком обчислювальної техніки інженерна практика наших днів все частіше і частіше зустрічається з математичними задачами, точний розв’язок яких отримати достатньо важко. В таких випадках зазвичай звертаються до тих чи інших наближених обчислень. Ось чому наближені і чисельні методи математичного аналізу отримали за останні роки широкий розвиток і набули виключно важливого значення.
Чисельне розв’язання прикладних задач завжди цікавило математиків. Аналіз ускладнених моделей вимагав створення спеціальних, як правило, чисельних або асимптотичних методів розв’язання завдань. Назви деяких з таких методів - методи Ньютона, Ейлера, Лобачевського, Гауса, Чебишева, Ерміта, Крилова - свідчать про те, що їх розробкою займалися найвидатніші вчені свого часу.
Чисельні методи є одним з могутніх математичних засобів розв’язання задач. Прості чисельні методи ми використовуємо скрізь, наприклад, при знаходженні квадратного кореня на листку паперу. Є завдання, де без достатньо складних чисельних методів не вдалося б отримати відповіді. Класичний приклад — відкриття Нептуна по аномаліях руху Урану.
Загалом у курсах чисельних методів вивчаються питання побудови, застосування і теоретичного обґрунтування алгоритмів наближеного розв’язання різних класів математичних задач. У наш час більшість обчислювальних алгоритмів орієнтовано на використання швидкодіючих ЕОМ, що значно впливає на підбір учбового матеріалу й на характер його викладу. Тільки обчислювальній машині під силу виконувати за короткий час об'єм обчислень в мільярди, трильйони і більше операції, які необхідні для вирішення багатьох сучасних завдань.
Варто відмітити деякі особливості предмету чисельних методів. По-перше, для чисельних методів характерна множинність, тобто можливість розв’язати одну й ту саму задачу різними методами. По-друге, природничонаукові задачі і швидкий розвиток обчислювальної техніки змушують переоцінювати значення існуючих алгоритмів і призводять до створення нових. По-третє, чисельні методи разом із можливістю отримання результату за прийнятний час не повинні вносити у обчислювальний процес значних похибок.
У даній курсовій роботі розглядається задача про інтерполяцію функції. Якщо задана функція y(x), то це означає, що будь-якому допустимому значенню х ставиться у відповідність значення у. Однак, нерідко виявляється, що знаходження цього значення дуже трудомістке. Наприклад, у(х) може бути визначене як розв’язок складної задачі, в якій х виконує роль параметра, або у(х) вимірюється в дорогому експерименті. При цьому можна обчислити невелику таблицю значень функції, але пряме знаходження функції при великому числі значень аргументу буде практично неможливо.
Функція у(х) може брати участь у будь-яких фізико-технічних або чисто математичних розрахунках,
де її доводиться багато разів обчислювати. У цьому випадку вигідно
замінити функцію у (х) наближеною відомою
функцією, тобто підібрати деяку функцію f(x), яка близька у певному сенсі до
у(х) і легко обчислюється. Потім при всіх значеннях аргументу вважають,
що ![]() .
.
Більша частина класичного чисельного аналізу ґрунтується на наближенні многочленами, оскільки з ними легко працювати. Однак для багатьох цілей використовують і інші класи функцій (див. [2]).
Вибравши вузлові точки і клас функцій, що наближають, ми повинні також вибрати одну певну функцію з цього класу за допомогою деякого критерію - міри наближення або «згоди». Перш, ніж почати обчислення, ми повинні вирішити також, яку точність ми хочемо мати у відповіді і який критерій ми оберемо для вимірювання цієї точності.
Все викладене можна сформулювати у вигляді чотирьох питань:
1. Які вузли ми будемо використовувати?
2. Який клас функцій для наближення будемо використовувати?
3. Який критерій згоди ми застосуємо?
4. Яку точність ми хочемо?
Існує 3 класи або групи функцій, широко застосовуваних у чисельному аналізі. Перша група включає в себе лінійні комбінації функцій 1, х, х2, ..., хn, що збігається з класом усіх многочленів степені n (або менше). Другий клас утворюють функції cos aix, sin aix. Цей клас має відношення до рядів Фур'є та інтегралу Фур'є. Третя група утворюється функціями e-az. Ці функції зустрічаються в реальних ситуаціях. До них, наприклад, призводять задачі накопичення і розпаду.
Що стосується критерію згоди, то класичним критерієм згоди є «точний збіг у вузлових точках». Цей критерій має перевагу завдяки простоті теорії та виконанню обчислень, але також незручність через ігнорування похибки (шуму), що виникає при вимірюванні або обчисленні значень у вузлових точках. Інший відносно хороший критерій - це «найменші квадрати». Він означає, що сума квадратів відхилень у вузлових точках повинна бути найменшою можливою або, іншими словами, мінімізована. Цей критерій використовує помилкову інформацію, щоб отримати деяке згладжування шуму. Третій критерій пов’язаний з ім'ям Чебишева. Основна ідея його полягає в тому, щоб зменшити максимальне відхилення до мінімуму. Очевидно, можливі й інші критерії. Більш конкретно відповісти на поставлені 4 питання можна лише виходячи з умов і мети кожної окремої задачі.
Розділ I. Інтерполювання функцій
Однією з основних задач чисельного аналізу являється задача про інтерполяцію функції. Багатьом з тих, хто стикається з науковими та інженерними розрахунками часто доводиться оперувати наборами значень, отриманих експериментальним шляхом чи методом випадкової вибірки. Як правило, на підставі цих наборів потрібно побудувати функцію, зі значеннями якої могли б з високою точністю збігатися інші отримувані значення. Така задача називається апроксимацією кривої.
Інтерполяцією називають такий різновид апроксимації, при якій крива побудованої функції проходить точно через наявні точки даних. Існує також близька до інтерполяції задача, що полягає в апроксимації якої-небудь складної функції іншою, більш простою функцією. Якщо деяка функція занадто складна для продуктивних обчислень, можна спробувати обчислити її значення в декількох точках, а по них побудувати, тобто інтерполювати, більш просту функцію. Зрозуміло, використання спрощеної функції не дозволяє одержати такі ж точні результати, які давала б початкова функція. Але, для деяких класів задач, досягнутий виграш у простоті і швидкості обчислень може переважити отриману похибку у результатах. Варто також згадати і зовсім інший різновид математичної інтерполяції, відому за назвою «інтерполяція операторів». До класичних робіт по інтерполяції операторів відносяться теорема Ріса-Торина і теорема Марцинкевича (див. [3]), що є основою для багатьох інших робіт. В результаті виникає наступна математична задача.
Нехай функція ![]() задана таблицею:
задана таблицею:
![]() .
.
Потрібно побудувати інтерполянту –
функцію ![]() , котра співпадає з функцією
, котра співпадає з функцією ![]() в
точках
в
точках ![]() :
:
![]() (1. 1. 1)
(1. 1. 1)
Основна мета інтерполяції – отримати
швидкий алгоритм обчислення значень ![]() і оцінити похибку
і оцінити похибку ![]() . Інтерполюючі
функції
. Інтерполюючі
функції ![]() , як правило, будуються в вигляді
лінійних комбінацій деяких елементарних функцій:
, як правило, будуються в вигляді
лінійних комбінацій деяких елементарних функцій:![]() , де
, де ![]() - фіксовані
лінійно незалежні функції,
- фіксовані
лінійно незалежні функції, ![]() - не визначені поки що
коефіцієнти.
- не визначені поки що
коефіцієнти.
Із умов (1. 1. 1) отримуємо систему п+1 рівнянь
відносно коефіцієнтів ![]() :
: ![]() .
.
Припустимо, що система функцій ![]() така,
що при будь-якому
така,
що при будь-якому ![]() відмінний від нуля визначник
системи:
відмінний від нуля визначник
системи:
 .
.
Тоді по заданим ![]() однозначно
визначаються коефіцієнти
однозначно
визначаються коефіцієнти ![]() . В якості системи лінійно
незалежних функцій
. В якості системи лінійно
незалежних функцій ![]() частіше обирають: степеневі
функції
частіше обирають: степеневі
функції ![]() (в цьому випадку
(в цьому випадку ![]() - поліном
степені п); тригонометричні функції
- поліном
степені п); тригонометричні функції ![]() (f - тригонометричний поліном);
використовують також раціональні функції та ін.
(f - тригонометричний поліном);
використовують також раціональні функції та ін.
В даній курсовій роботі розглядаються інтерполяційні поліноми.
Відомо, що будь-яка неперервна на
відрізку ![]() функція
функція ![]() може бути добре
наближена деяким поліномом
може бути добре
наближена деяким поліномом ![]() (див. [1], c.50):
(див. [1], c.50):
Теорема Вейерштрасса: Для будь-якого ![]() існує
поліном
існує
поліном ![]() степеня
степеня ![]() , такий, що
, такий, що ![]() .
.
Отже, будемо шукати інтерполяційний поліном в вигляді:
![]() , (1. 1. 2)
, (1. 1. 2)
де ![]() - невизначені коефіцієнти.
Покладемо
- невизначені коефіцієнти.
Покладемо ![]() , тоді отримаємо систему лінійних
рівнянь:
, тоді отримаємо систему лінійних
рівнянь:
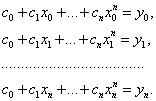
Визначник даної системи являється відмінним від нуля визначником Вандермонда (див. [9]):
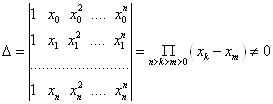 .
.
Звідси випливає, що інтерполяційний поліном (1. 1. 2) існує і він єдиний, хоча форм його запису існує багато.
В
якості базису ![]() ми взяли базис із одночленів
ми взяли базис із одночленів ![]() . Для
обчислень більш зручним являється базис поліномів Лагранжа
. Для
обчислень більш зручним являється базис поліномів Лагранжа ![]() степеня п або
коефіцієнтів Лагранжа:
степеня п або
коефіцієнтів Лагранжа:
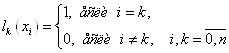
Неважко побачити, що поліном степені п
![]()
задовольняє
цим умовам. Полином ![]() , очевидно, визначається єдиним
способом. Дійсно, нехай існує ще один поліном
, очевидно, визначається єдиним
способом. Дійсно, нехай існує ще один поліном ![]() , тоді їх різниця
, тоді їх різниця ![]() є поліном
степені п, який перетворюється в нуль в п+1 точках
є поліном
степені п, який перетворюється в нуль в п+1 точках ![]() . Це можливо тільки при
. Це можливо тільки при ![]() .
.
Поліном
![]() приймає
значення
приймає
значення ![]() в точці
в точці ![]() і рівний нулю у всіх
останніх вузлах
і рівний нулю у всіх
останніх вузлах ![]() при
при ![]() . Звідси випливає, що
інтерполяційний поліном:
. Звідси випливає, що
інтерполяційний поліном:
![]() (1.
1. 3)
(1.
1. 3)
має
степінь не вище п і ![]() . Формулу (1. 1. 3) називають формулою Лагранжа. Число
арифметичних дій для обчислення по (1. 1. 3) пропорційно
. Формулу (1. 1. 3) називають формулою Лагранжа. Число
арифметичних дій для обчислення по (1. 1. 3) пропорційно ![]() . Для оцінки близькості полінома
. Для оцінки близькості полінома ![]() до
функції
до
функції ![]() покладають, що існує п+1– ша
неперервна похідна
покладають, що існує п+1– ша
неперервна похідна ![]() . Тоді має місце формула для
похибки
. Тоді має місце формула для
похибки
 .
.
При оцінці похибки результатів повинні враховуватись як похибки методу інтерполяції (залишковий член), так і похибка округлення при обчисленнях.
1.2 Інтерполяційні формули Ньютона
Часто інтерполювання ведеться для
функцій, заданих таблицями з рівновіддаленими значеннями аргументу (тобто
такими, що будь-який ![]() (вузол інтерполяції) можна
представити у вигляді
(вузол інтерполяції) можна
представити у вигляді ![]() - деяка постійна величина, яка називається
кроком інтерполяції). Для таких таблиць побудова інтерполяційних формул, а
також проведення обчислень по ним значно спрощується.
- деяка постійна величина, яка називається
кроком інтерполяції). Для таких таблиць побудова інтерполяційних формул, а
також проведення обчислень по ним значно спрощується.
Для побудови формули Ньютона необхідно ввести поняття кінцевих різниць.
Кінцевими різницями називають різниці
між значеннями функції в сусідніх вузлах (точках ![]() ) інтерполяції:
) інтерполяції:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

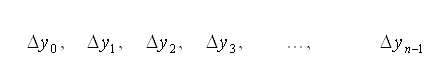
де ![]() Отримані кінцеві різниці
будемо називати кінцевими різницями першого порядку. З різниць першого порядку
отримаємо різниці другого порядку:
Отримані кінцеві різниці
будемо називати кінцевими різницями першого порядку. З різниць першого порядку
отримаємо різниці другого порядку:
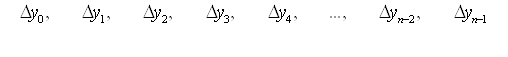

![]()
![]()
![]()
![]()
![]()

![]()

![]()

![]()
де ![]()
![]() .
.
Повторюючи процедуру, отримаємо кінцеві різниці третього порядку:
![]()
![]()
Для кінцевих різниць ![]() -го порядку:
-го порядку:
![]()
![]()
В результаті отримаємо таблицю кінцевих різниць:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
.............
![]()
Залучивши визначення похідної, можна
виявити певний зв'язок між кінцевими різницями і похідними. А саме, якщо
враховувати, що ![]() , то можна сказати, що при
достатньо малих
, то можна сказати, що при
достатньо малих ![]() має місце наближена рівність
має місце наближена рівність
![]() тобто перші різниці характеризують
першу похідну функції
тобто перші різниці характеризують
першу похідну функції ![]() по значенням якої вони складені.
Скориставшись цим, маємо для других різниць:
по значенням якої вони складені.
Скориставшись цим, маємо для других різниць: ![]()
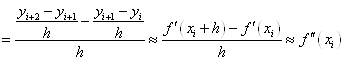 ,
,
тобто ![]() , і, взагалі,
, і, взагалі, ![]() . (1.
2. 1)
. (1.
2. 1)
Таким чином, на кінцеві різниці можна дивитись як на деякий аналог похідних. Звідси справедливість багатьох їх властивостей, однакових зі властивостями похідних.
Відмітимо лише найпростіші властивості кінцевих різниць:
1. кінцеві різниці сталої дорівнюють нулю;
2. сталий множник у функції можна виносити за знак кінцевої різниці;
3. кінцева різниця від суми двох функцій дорівнює сумі їх кінцевих різниць в одній і тій же точці.
Враховуючи роль, яку відіграють многочлени в теорії інтерполювання, подивимось, що представляють собою кінцеві різниці многочленна.
Так як многочлен в своїй канонічній
формі є лінійна комбінація степеневих функцій, покладемо спочатку ![]() . Використовуючи
біноміальне розвинення п-ого степеня двочлена, отримаємо:
. Використовуючи
біноміальне розвинення п-ого степеня двочлена, отримаємо:
![]()
тобто перша кінцева різниця
степеневої функції ![]() є многочлен степеня п-1 зі
старшим членом
є многочлен степеня п-1 зі
старшим членом ![]() . Якщо взяти тепер кінцеву різницю
від функції
. Якщо взяти тепер кінцеву різницю
від функції
![]() , (1. 2. 2)
, (1. 2. 2)
то в силу лінійних властивостей ![]() , можна записати
, можна записати ![]() . Перший доданок в цій сумі, як
з’ясовано, є многочлен (п-1)-го степеня, другий, аналогічно, - многочлен
степеня п-2, і т. д. отже, перша кінцева різниця многочленна (1. 2. 2) в точці
. Перший доданок в цій сумі, як
з’ясовано, є многочлен (п-1)-го степеня, другий, аналогічно, - многочлен
степеня п-2, і т. д. отже, перша кінцева різниця многочленна (1. 2. 2) в точці ![]() з короком
з короком ![]() є многочлен зі старшим членом
є многочлен зі старшим членом ![]() ,
друга кінцева різниця – многочлен зі старшим членом
,
друга кінцева різниця – многочлен зі старшим членом ![]() , …,
, …, ![]() -та різниця –
многочлен зі старшим членом
-та різниця –
многочлен зі старшим членом ![]() .
.
При ![]() отримуємо постійну різницю п-го
порядку
отримуємо постійну різницю п-го
порядку ![]() для многочлена (1. 2. 2), кінцеві
різниці більш високих порядків дорівнюють нулю.
для многочлена (1. 2. 2), кінцеві
різниці більш високих порядків дорівнюють нулю.
Тобто, головний висновок із попередніх роздумів: п-і кінцеві різниці многочленна п-ого степеня постійні, а (п+1)-ші і всі наступні рівні нулю.
Однак, більш важливим для розуміння
суті поліноміального інтерполювання є твердження, обернене зробленому вище
висновку. А саме, що якщо кінцеві різниці п-го порядку деякої функції ![]() постійні
в будь-якій точці
постійні
в будь-якій точці ![]() при різних фіксованих кроках
при різних фіксованих кроках ![]() , то
ця функція
, то
ця функція ![]() є многочлен степеня п.
є многочлен степеня п.
Для функції ![]() , заданої таблицею своїх
значень
, заданої таблицею своїх
значень ![]() у вузлах
у вузлах ![]() , де
, де ![]() , кінцеві
різниці різних порядків зручно поміщати в одну загальну таблицю з вузлами і
значеннями функції. Цю загальну таблицю називають таблицею кінцевих різниць.
, кінцеві
різниці різних порядків зручно поміщати в одну загальну таблицю з вузлами і
значеннями функції. Цю загальну таблицю називають таблицею кінцевих різниць.
1.2.1 Перша інтерполяційна формула Ньютона
Нехай для функції ![]() задані значення
задані значення ![]() для рівновіддалених значень
незалежної змінної:
для рівновіддалених значень
незалежної змінної: ![]() , де
, де ![]() - крок інтерполяції. Необхідно
підібрати поліном
- крок інтерполяції. Необхідно
підібрати поліном ![]() степені не вище п, який
приймає в точках
степені не вище п, який
приймає в точках ![]() значення
значення
![]() (1. 2. 3)
(1. 2. 3)
Умови (1. 2. 3) еквівалентні тому, що ![]() .
Слідуючи Ньютону, будемо шукати поліном у вигляді
.
Слідуючи Ньютону, будемо шукати поліном у вигляді

Використовуючи загальний степінь, вираз (1. 2. 3) запишемо так:
![]()
Наша задача заклечається у визначенні
коефіцієнтів ![]() полінома
полінома ![]() . Покладаючи
. Покладаючи ![]() у вираз (1. 2. 5), отримаємо
у вираз (1. 2. 5), отримаємо ![]() .
.
Щоб знайти коефіцієнт ![]() , складемо
першу кінцеву різницю
, складемо
першу кінцеву різницю ![]() . Припускаючи в останньому виразі
. Припускаючи в останньому виразі ![]() , отримаємо:
, отримаємо: ![]() ; звідки
; звідки ![]() . Для визначення коефіцієнта
. Для визначення коефіцієнта ![]() складемо кінцеву різницю другого
порядку
складемо кінцеву різницю другого
порядку ![]() .
Покладаючи
.
Покладаючи ![]() , отримаємо:
, отримаємо: ![]() ; звідки
; звідки ![]() . Послідовно продовжуючи цей процес,
ми виявимо, що
. Послідовно продовжуючи цей процес,
ми виявимо, що ![]() , де
, де ![]() .
.
Підставляючи знайдені значення
коефіцієнтів ![]() у вираз (1. 2. 5) отримаємо
інтерполяційний поліном Ньютона
у вираз (1. 2. 5) отримаємо
інтерполяційний поліном Ньютона
![]() . (1. 2. 6)
. (1. 2. 6)
Легко побачити, що поліном (1. 2. 6.)
повністю задовольняє вимогам поставленої задачі. Дійсно, по-перше, степінь
поліному ![]() не вище п, по-друге,
не вище п, по-друге, ![]() і
і
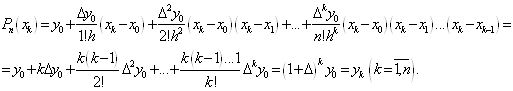
Замітимо, що при ![]() формула (1. 2.
6) перетворюється в ряд Тейлора для функції
формула (1. 2.
6) перетворюється в ряд Тейлора для функції ![]() . Дійсно,
. Дійсно,  Крім того, очевидно,
Крім того, очевидно, ![]() .
Звідси при
.
Звідси при ![]() формула (1. 2. 6) приймає вид поліному
Тейлора:
формула (1. 2. 6) приймає вид поліному
Тейлора: ![]() .
.
Для практичного використання
інтерполяційну формулу Ньютона (1. 2. 6) зазвичай записують в дещо
перетвореному вигляді. Для цього введемо нову змінну ![]() за формулою
за формулою ![]() ; тоді
; тоді
![]()
підставляючи ці вирази у формулу (1. 2. 6), отримаємо:
![]() , (1. 2. 7)
, (1. 2. 7)
де ![]() являє собою кількість кроків,
необхідних для досягнення точки
являє собою кількість кроків,
необхідних для досягнення точки ![]() , виходячи із точки
, виходячи із точки ![]() . Це і є
кінцевий вигляд першої інтерполяційної формули Ньютона.
. Це і є
кінцевий вигляд першої інтерполяційної формули Ньютона.
Формулу (1. 2. 7) вигідно
використовувати для інтерполювання функції в околі початкового значення ![]() , де
, де ![]() мале
за абсолютною величиною.
мале
за абсолютною величиною.
Якщо у формулі (1. 2. 7) покласти
п=1, то отримаємо формулу лінійного інтерполювання: ![]() . При п=2 будемо мати формулу
параболічного або квадратичного інтерполювання
. При п=2 будемо мати формулу
параболічного або квадратичного інтерполювання
![]() .
.
Якщо дана необмежена таблиця значень ![]() , то
число
, то
число ![]() в інтерполяційній формулі (1. 2.
7) може бути довільним. Практично в цьому випадку число
в інтерполяційній формулі (1. 2.
7) може бути довільним. Практично в цьому випадку число ![]() обирають так, щоб
різниця
обирають так, щоб
різниця ![]() була постійною із заданою
точністю. За початкове значення
була постійною із заданою
точністю. За початкове значення ![]() можна приймати довільне табличне
значення аргументу
можна приймати довільне табличне
значення аргументу ![]() .
.
Якщо таблиця значень функції
скінчена, то ![]() - число обмежене, а саме:
- число обмежене, а саме: ![]() не
може бути більше числа значень функції
не
може бути більше числа значень функції ![]() , зменшеного на одиницю.
, зменшеного на одиницю.
Відзначимо, що при застосуванні першої інтерполяційної формули Ньютона зручно використовувати горизонтальну таблицю різниць, так як потрібні значення різниць функції знаходяться у відповідному горизонтальному рядку таблиці.
1.2.2 Друга інтерполяційна формула Ньютона
Перша інтерполяційна формула Ньютона практично незручна для інтерполювання функції поблизу вузлів таблиці. В такому випадку зазвичай застосовують другу інтерполяційну формулу Ньютона. Виведемо цю формулу.
Нехай маємо систему значень функції ![]() для
рівновіддалених значень аргументу
для
рівновіддалених значень аргументу ![]() , де
, де ![]() - крок інтерполяції.
Побудуємо поліном наступного вигляду:
- крок інтерполяції.
Побудуємо поліном наступного вигляду:
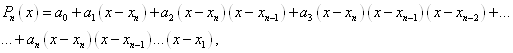
або, використовуючи узагальнену степінь, отримуємо:
![]() . (1. 2. 8)
. (1. 2. 8)
Наша задача полягає у визначенні
коефіцієнтів ![]() таким чином, щоб виконувались умови
(1. 2. 3). Для цього необхідно і достатньо, щоб
таким чином, щоб виконувались умови
(1. 2. 3). Для цього необхідно і достатньо, щоб
![]() (1. 2. 9)
(1. 2. 9)
Покладемо ![]() у формулі (1. 2. 8). Тоді будемо
мати:
у формулі (1. 2. 8). Тоді будемо
мати: ![]() ,
отже
,
отже ![]() .
.
Далі беремо від лівої і правої формули (1. 2. 8) кінцеві різниці першого порядку
![]() .
.
Звідси, вважаючи ![]() і враховуючи відношення
(1. 2. 9) будемо мати:
і враховуючи відношення
(1. 2. 9) будемо мати:
![]() . Отже
. Отже ![]() .
.
Покладаючи ![]() знаходимо:
знаходимо: ![]() . І таким чином
. І таким чином ![]() .
.
Характер закономірності коефіцієнтів ![]() достатньо
зрозумілий. Застосовуючи метод математичної індукції, можна строго довести, що
достатньо
зрозумілий. Застосовуючи метод математичної індукції, можна строго довести, що
![]() (1. 2. 10)
(1. 2. 10)
Підставляючи ці значення у формулу (1. 2. 8) будемо мати остаточно
![]()
![]() (1. 2. 11)
(1. 2. 11)
Формула (1. 2. 11) носить назву другої інтерполяційної формули Ньютона.
Введемо більш зручний запис формули (1.
2. 11). Нехай ![]() , тоді
, тоді
![]() і т. д.
і т. д.
Підставивши ці значення у формулу (1. 2. 11), отримаємо:
![]()
![]() . (1.2.12)
. (1.2.12)
Це і є загальний вигляд другої
інтерполяційної формули Ньютона. Для наближеного обчислення значень функції ![]() вважають,
що
вважають,
що ![]() .
.
Як перша, так и друга інтерполяційні
формули Ньютона можуть бути використані для екстраполяції, тобто, для
знаходження значень функції ![]() для значень аргументів
для значень аргументів ![]() ,
котрі лежать за межами таблиці. Якщо
,
котрі лежать за межами таблиці. Якщо ![]() і
і ![]() близько до
близько до ![]() , то
вигідно використовувати першу інтерполяційну формулу Ньютона, причому тоді
, то
вигідно використовувати першу інтерполяційну формулу Ньютона, причому тоді ![]() . Якщо
ж
. Якщо
ж ![]() і
і
![]() близько
до
близько
до ![]() ,
то зручніше використовувати другу інтерполяційну формулу Ньютона, причому тоді
,
то зручніше використовувати другу інтерполяційну формулу Ньютона, причому тоді ![]() .
Таким чином, перша інтерполяційна формула Ньютона використовується для
інтерполяції вперед і екстраполяції назад, а друга інтерполяційна формула
Ньютона, навпаки, – для інтерполяції назад і екстраполяції вперед (див. [8]).
.
Таким чином, перша інтерполяційна формула Ньютона використовується для
інтерполяції вперед і екстраполяції назад, а друга інтерполяційна формула
Ньютона, навпаки, – для інтерполяції назад і екстраполяції вперед (див. [8]).
Відмітимо, що операція екстраполяції, взагалі кажучи, менш точна, ніж операція інтерполяції у вузькому значенні слова.
1.2.3 Оцінка похибок інтерполяційних формул Ньютона
Для функції ![]() ми побудували
інтерполяційний поліном Ньютона
ми побудували
інтерполяційний поліном Ньютона ![]() , який приймає в точках
, який приймає в точках ![]() задані
значення
задані
значення ![]() . Виникає питання, наскільки
близько побудований поліном наближається до функції
. Виникає питання, наскільки
близько побудований поліном наближається до функції ![]() в інших точках, тобто
наскільки великий залишковий член
в інших точках, тобто
наскільки великий залишковий член ![]() . Для визначення цього степеня наближення накладемо на функцію
. Для визначення цього степеня наближення накладемо на функцію
![]() додаткові
обмеження. А саме, ми будемо припускати, що в області зміни
додаткові
обмеження. А саме, ми будемо припускати, що в області зміни ![]() :
: ![]() ,
котра містить вузли інтерполювання, функція
,
котра містить вузли інтерполювання, функція ![]() має всі похідні
має всі похідні ![]() до (п+1)-го порядку
включаючи.
до (п+1)-го порядку
включаючи.
Введемо допоміжну функцію
![]() , (1. 2. 12) де
, (1. 2. 12) де ![]() і
і
![]() - постійний коефіцієнт, котрий буде
обрано нижче.
- постійний коефіцієнт, котрий буде
обрано нижче.
Функція ![]() , очевидно, має п+1 корінь в точках
, очевидно, має п+1 корінь в точках ![]() . Підберемо тепер коефіцієнт
. Підберемо тепер коефіцієнт ![]() таким
чином, щоб
таким
чином, щоб ![]() мала (п+2)-ий корінь в будь-якій,
але фіксованій точці відрізка
мала (п+2)-ий корінь в будь-якій,
але фіксованій точці відрізка ![]() , яка не співпадає з вузлами
інтерполювання (мал. 1). Для цього достатньо покласти
, яка не співпадає з вузлами
інтерполювання (мал. 1). Для цього достатньо покласти
![]() .
.
Звідси, так як ![]() , то
, то
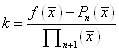 (1. 2. 13)
(1. 2. 13)
При цьому значення множника ![]() функції
функції ![]() має п+2 кореня на
відрізку
має п+2 кореня на
відрізку ![]() і буде обертатись в нуль на
кінцях кожного з відрізків
і буде обертатись в нуль на
кінцях кожного з відрізків
![]() . Застосовуючи теорему Ролля [11] до кожного із цих відрізків,
переконуємось, що похідна
. Застосовуючи теорему Ролля [11] до кожного із цих відрізків,
переконуємось, що похідна ![]() має не менше п+1 кореня на
відрізку
має не менше п+1 кореня на
відрізку ![]() .
.
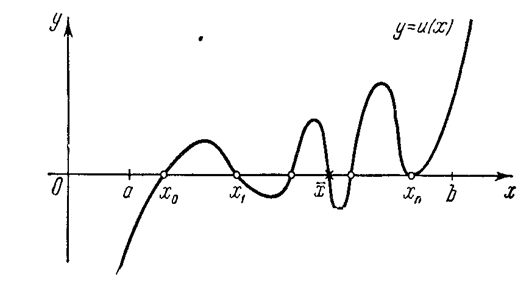
Малюнок 1. Графік функції ![]()
Застосовуючи теорему Ролля до
похідної ![]() , ми
переконаємося, що друга похідна
, ми
переконаємося, що друга похідна ![]() перетворюється в нуль не менше п
разів на відрізку
перетворюється в нуль не менше п
разів на відрізку ![]() .
.
Продовжуючи ці роздуми, прийдемо до
висновку, що на відрізку ![]() похідна
похідна ![]() має хоча б один корінь,
котрий позначимо через
має хоча б один корінь,
котрий позначимо через ![]() , тобто
, тобто ![]() .
.
Із формули (1. 2. 11) так як ![]() , маємо:
, маємо: ![]() . При
. При ![]() , отримуємо:
, отримуємо: ![]() Звідси
Звідси
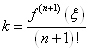 .
(1. 2. 14)
.
(1. 2. 14)
Порівнюючи праві частини формул (1. 2. 13) і (1. 2. 14), будемо мати:
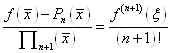 , тобто
, тобто
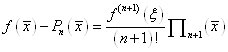 . (1. 2. 15)
. (1. 2. 15)
Так як ![]() довільне, то формулу (1. 2. 15) можна записати і так:
довільне, то формулу (1. 2. 15) можна записати і так:
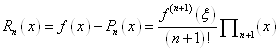 , (1. 2. 16)
, (1. 2. 16)
де ![]() залежить від
залежить від ![]() і лежить всередині відрізка
і лежить всередині відрізка ![]() .
.
Відмітимо, що формула (1. 2. 16) справедлива для всіх точок
відрізка ![]() , в тому числі і для вузлів
інтерполювання.
, в тому числі і для вузлів
інтерполювання.
На основі формули (1. 2. 16) отримаємо залишковий член першої інтерполяційної формули Ньютона:
![]() , (1. 2. 17)
, (1. 2. 17)
де ![]() - деяка внутрішня точка
найменшого проміжку, що містить всі вузли
- деяка внутрішня точка
найменшого проміжку, що містить всі вузли ![]() і точку
і точку ![]() .
.
Аналогічно, покладаючи в формулі (1. 2. 17) ![]() , отримаємо залишковий член другої
інтерполяційної формули Ньютона:
, отримаємо залишковий член другої
інтерполяційної формули Ньютона:
![]() , (1. 2. 18)
, (1. 2. 18)
де ![]() - деяка внутрішня точка
найменшого проміжку, що містить всі вузли
- деяка внутрішня точка
найменшого проміжку, що містить всі вузли ![]() і точку
і точку ![]() .
.
Зазвичай при практичних обчисленнях інтерполяційна формула Ньютона обривається на членах, що містять такі різниці, які в межах заданої точності можна вважати постійними.
Вважаючи, що ![]() майже постійними для
функції
майже постійними для
функції ![]() і
і ![]() достатньо малим, і
враховуючи, що
достатньо малим, і
враховуючи, що ![]() , наближено можна покласти:
, наближено можна покласти:
![]() .
.
В цьому випадку залишковий член першої інтерполяційної формули Ньютона наближено рівний
![]() .
.
При таких самих умовах для залишкового члена другої інтерполяційної формули Ньютона отримаємо вираз
![]() .
.
1.3 Інтерполяційні формули Гауса
При побудові інтерполяційних формул Ньютона використовуються лише значення функції, що лежать з однієї сторони початкового наближення, тобто, ці формули носять односторонній характер (див.[3]).
В багатьох випадках виявляються
корисними інтерполяційні формули, що містять як наступні, так і попередні
значення функції по відношенню до її початкового наближеного значення. Найбільш
вживаними серед них являються ті, що містять різниці, розміщені у
горизонтальному рядку діагональної таблиці різниць даної функції, що відповідає
початковим значенням ![]() і
і ![]() , або в рядках, що безпосередньо
примикають до неї. Ці різниці
, або в рядках, що безпосередньо
примикають до неї. Ці різниці ![]() називаються центральними різницями,
причому
називаються центральними різницями,
причому ![]() і т. д.
і т. д.
Відповідні їм формули називають інтерполяційними формулами із центральними різницями. До їх числа відносяться формули Гауса, Стірлінга і Бесселя.
Постановка задачі. Нехай маємо 2п+1 рівновіддалені вузли інтерполяції:
![]() ,
,
де ![]() , і для функції
, і для функції ![]() відомі її значення в цих вузлах
відомі її значення в цих вузлах ![]() , потрібно побудувати такий поліном
, потрібно побудувати такий поліном ![]() степені
не вище 2п, що
степені
не вище 2п, що ![]() . Із останньої умови
випливає, що
. Із останньої умови
випливає, що
![]() (1. 3. 1)
(1. 3. 1)
для всіх відповідних значень і та k.
Будемо шукати поліном у вигляді:

Вводячи узагальнені степені (див [3]), отримаємо:

Застосовуючи для обчислення
коефіцієнтів ![]() такий
же спосіб, що і при виведенні інтерполяційних формул Ньютона, і враховуючи
формулу (1. 3. 1), послідовно знаходимо:
такий
же спосіб, що і при виведенні інтерполяційних формул Ньютона, і враховуючи
формулу (1. 3. 1), послідовно знаходимо:
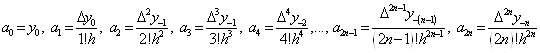
Далі вводячи змінну ![]() і зробивши
відповідну заміну у формулі (1. 3. 3), отримаємо першу інтерполяційну формулу
Гауса:
і зробивши
відповідну заміну у формулі (1. 3. 3), отримаємо першу інтерполяційну формулу
Гауса:

або, коротше,

де ![]() .
.
Перша інтерполяційна формула Гауса містить центральні різниці
![]() .
.
Аналогічно можна отримати другу
інтерполяційну формулу Гауса, котра містить центральні різниці ![]() . Друга інтерполяційна формула Гауса
має вигляд:
. Друга інтерполяційна формула Гауса
має вигляд:

або, в скорочених позначеннях,

де ![]() .
.
Формули Гауса застосовуються для
інтерполювання в середині таблиці поблизу ![]() . При цьому перша формула Гауса
застосовується при
. При цьому перша формула Гауса
застосовується при ![]() , а друга – при
, а друга – при ![]() .
.
1.4 Інтерполяційна формула Бесселя
Для того, щоб вивести формулу Бесселя використаємо другу інтерполяційну формулу Гауса (1. 3. 6).
Візьмемо ![]() рівновіддалених вузлів
інтерполювання
рівновіддалених вузлів
інтерполювання ![]() з кроком
з кроком ![]() , і нехай
, і нехай ![]() - задані
значення функції
- задані
значення функції ![]() .
.
Якщо обрати за початкове значення ![]() і
і ![]() , то,
використовуючи вузли
, то,
використовуючи вузли ![]() , будемо мати:
, будемо мати:

прикладний задача інтерполяційний формула
Візьмемо тепер за початкове значення ![]() і
і ![]() і
використаємо вузли
і
використаємо вузли ![]() . Тоді
. Тоді ![]() , причому відповідно
індекси всіх різниць в правій частині формули (1. 4. 1) зростуть на одиницю. Якщо
замінити в правій частині формули (1. 4. 1)
, причому відповідно
індекси всіх різниць в правій частині формули (1. 4. 1) зростуть на одиницю. Якщо
замінити в правій частині формули (1. 4. 1) ![]() на
на ![]() і збільшивши індекси
всіх різниць на 1, отримаємо допоміжну інтерполяційну формулу:
і збільшивши індекси
всіх різниць на 1, отримаємо допоміжну інтерполяційну формулу:
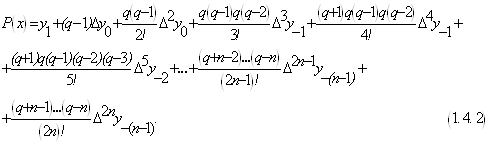
Взявши середнє арифметичне формул (1. 4. 1) і (1. 4. 2), після нескладних перетворень отримаємо інтерполяційну формулу Бесселя:
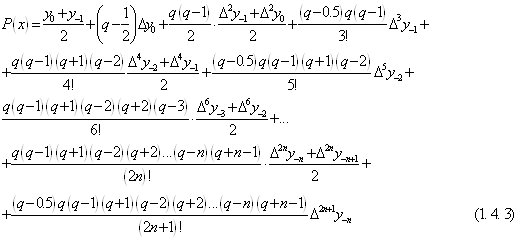
де ![]() .
.
Тобто, інтерполяційна формула Бесселя
(1. 4. 3), як слідує із способу отримання її, представляє собою поліном, який
співпадає з даною функцією ![]() в
в ![]() точках
точках ![]() .
.
В окремому випадку, при п=1, нехтуючи
різницею ![]() , маємо формулу квадратичної
інтерполяції по Бесселю:
, маємо формулу квадратичної
інтерполяції по Бесселю:
![]()
або ![]() , де
, де ![]() .
.
У формулі Бесселя всі члени, котрі
містять різниці непарного порядку, мають множник ![]() , тому при
, тому при ![]() формула (1. 4. 3) значно
спрощується:
формула (1. 4. 3) значно
спрощується:
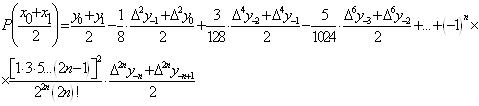
Цей спеціальний випадок формули Бесселя
називається формулою інтерполювання на середину. Якщо у формулі (1. 4. 3)
зробити заміну змінної за формулою ![]() , то вона приймає більш симетричний
вигляд:
, то вона приймає більш симетричний
вигляд:

де ![]() .
.
Формула Бесселя використовується для
інтерполювання всередині таблиці при значеннях q, близьких до 0.5. Практично
вона використовується при ![]() .
.
1.5 Інтерполяційна формула Стірлінга
Якщо взяти середнє арифметичне першої інтерполяційної формули Гауса (1. 3. 4) та другої формули Гауса (1. 3. 6), то отримаємо формулу Стірлінга:

де ![]() .
.
Легко бачити, що ![]() при
при ![]() .
.
Формула Стірлінга використовується
для інтерполювання в середині таблиці при значеннях ![]() , близьких до нуля.
Практично її використовують при
, близьких до нуля.
Практично її використовують при ![]() .
.
1.6 Оцінки похибок центральних інтерполяційних формул
Приведемо залишкові члени для формул Гауса, Стірлінга і Бесселя [12].
1. Залишковий член інтерполяційних формул Гауса (1. 3. 4) і (1. 3. 6) та інтерполяційної формули Стірлінга (1. 5. 1).
Якщо 2п – порядок максимальної різниці таблиці, яка використовується
і ![]() , то
, то 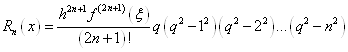 ,
,
де ![]() .
.
Якщо ж аналітичний вираз функції ![]() невідомий,
то при
невідомий,
то при ![]() малому покладають [2]:
малому покладають [2]: ![]() .
.
2. Залишковий член інтерполяційної формули Бесселя (1. 4. 3).
Якщо 2п+1 – порядок максимальної
використовуваної різниці таблиці і ![]() , то
, то
![]() ,
,
де ![]() .
.
Якщо ж функція ![]() задана таблично і крок h малий, то приймають:
задана таблично і крок h малий, то приймають:
![]() .
.
Найбільш простий вигляд формула має при q=0.5, так як всі члени, що містять різниці непарного порядку зникають. Цей спеціальний випадок формули Бесселя називається формулою інтерполювання на середину. Її використовують для ущільнення таблиць [4], тобто для складання таблиць з більш малим кроком. Для залишкового члена при q=0.5 маємо:
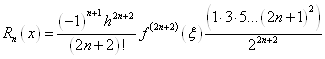 .
.
1.7 Інтерполяційна формула Ньютона для нерівновіддалених вузлів
Для побудови інтерполяційних формул у
випадку довільного розташування упорядкованих не співпадаючих вузлів ![]() на
проміжку
на
проміжку ![]() , замість кінцевих різниць
використовують розділені різниці, або інакше, різницеві відношення.
, замість кінцевих різниць
використовують розділені різниці, або інакше, різницеві відношення.
Через значення функції ![]() спочатку
визначають розділені різниці першого порядку:
спочатку
визначають розділені різниці першого порядку:
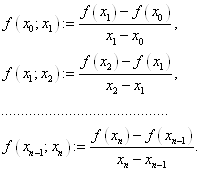 (1. 7. 1)
(1. 7. 1)
На різницях (1. 7. 1) шукаються розділені різниці другого порядку:
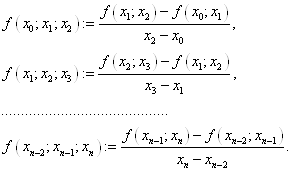
і т.д. Таким чином, якщо визначені
k-ті різницеві відношення ![]() , то
, то ![]() - ті визначаються завдяки ним рівністю:
- ті визначаються завдяки ним рівністю:
![]() (1. 7. 2)
(1. 7. 2)
Нехай ![]() - деяка функція із
відомими значеннями у вузлах
- деяка функція із
відомими значеннями у вузлах ![]() , а
, а ![]() - довільна фіксована
точка. За означенням розділеної різниці першого порядку (1. 7. 1) маємо:
- довільна фіксована
точка. За означенням розділеної різниці першого порядку (1. 7. 1) маємо: ![]() звідки
звідки
![]() (1. 7. 3)
(1. 7. 3)
Для розділеної різниці другого
порядку по точкам ![]() записуємо представлення:
записуємо представлення: ![]() наслідком
якого являється вираз
наслідком
якого являється вираз ![]() Підставляючи його у формулу (1. 7. 2),
приходимо до рівності
Підставляючи його у формулу (1. 7. 2),
приходимо до рівності
![]()
Формально, на основі рекурентного
відношення (1. 7. 2) цей процес може бути продовжений. В результаті можна
записати формулу, яка описує своєрідне розкладання ![]() по добуткам різниць
по добуткам різниць ![]() ,
коефіцієнтами якого являються розділені різниці різних порядків:
,
коефіцієнтами якого являються розділені різниці різних порядків:
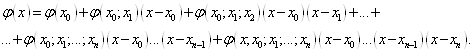 (1. 7. 4)
(1. 7. 4)
Якщо ![]() - многочлен степені п,
то процес подібного розкладання вичерпується. Розкладання буде складатись з п+1
доданка, і всі вони будуть мати конкретні коефіцієнти, так як остання, яка
містить
- многочлен степені п,
то процес подібного розкладання вичерпується. Розкладання буде складатись з п+1
доданка, і всі вони будуть мати конкретні коефіцієнти, так як остання, яка
містить ![]() , розділена різниця в (1. 7. 4), тобто
, розділена різниця в (1. 7. 4), тобто ![]() має (п+1)-ий
порядок і, значить, дорівнює нулю. Таким чином, для довільного многочленна
степені п справедлива тотожність
має (п+1)-ий
порядок і, значить, дорівнює нулю. Таким чином, для довільного многочленна
степені п справедлива тотожність
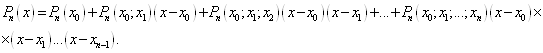
Припустимо, що цей многочлен ![]() являється
інтерполяційним для деякої функції
являється
інтерполяційним для деякої функції ![]() . Тоді у всіх вузлах
. Тоді у всіх вузлах ![]() він
повинен мати однакові з нею значення, а отже повинні бути однаковими і їх
розділені різниці. Звідси приходимо до інтерполяційної формули Ньютона для
нерівновіддалених вузлів:
він
повинен мати однакові з нею значення, а отже повинні бути однаковими і їх
розділені різниці. Звідси приходимо до інтерполяційної формули Ньютона для
нерівновіддалених вузлів:

Підставивши ![]() замість
замість ![]() у формулу (1. 7. 4), з урахуванням (1. 7. 5) отримуємо точну рівність
у формулу (1. 7. 4), з урахуванням (1. 7. 5) отримуємо точну рівність
![]()
другий доданок якої може розглядатись в якості залишкового члена, тобто
![]() , (1. 7. 6)
, (1. 7. 6)
де ![]() .
.
Так як для обчислення різниці ![]() необхідно
знання значення
необхідно
знання значення ![]() поряд з відомими значеннями
поряд з відомими значеннями ![]() ,
представлений формулою (1. 7. 5)
вираз
,
представлений формулою (1. 7. 5)
вираз ![]() фактично можна використовувати
тільки для оцінювання похибки інтерполювання за формулою (1. 7. 5) через максимальні величини модулів
розділених різниць (п+1)-го порядку або для одержання інших виразів залишкового
члена при тих чи інших припущеннях про дану функцію. Зокрема, якщо функція
фактично можна використовувати
тільки для оцінювання похибки інтерполювання за формулою (1. 7. 5) через максимальні величини модулів
розділених різниць (п+1)-го порядку або для одержання інших виразів залишкового
члена при тих чи інших припущеннях про дану функцію. Зокрема, якщо функція ![]() має
(п+1)-шу похідну, то залишковий член (1. 7. 6) може бути приведений до вигляду
має
(п+1)-шу похідну, то залишковий член (1. 7. 6) може бути приведений до вигляду 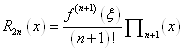 .
.
При практичному використання
інтерполяційної формули (1. 7. 5) доводиться покладатися на зменшення модулів доданків ![]() при
збільшенні номера доданка. Таке зменшення відбувається до деяких пір; потім
починається зростання їх модулів із-за впливу похибок заокруглення.
при
збільшенні номера доданка. Таке зменшення відбувається до деяких пір; потім
починається зростання їх модулів із-за впливу похибок заокруглення.
1.8 Приклади застосування інтерполяційних формул
1.8.1 Приклад 1
Використовуючи першу і другу
інтерполяційну формулу Ньютона і Гауса, а також інтерполяційні формули
Стірлінга і Бесселя необхідно знайти значення функції ![]() , заданої таблицею (табл. 1) при
значенні аргументу
, заданої таблицею (табл. 1) при
значенні аргументу ![]() . При цьому крок
. При цьому крок ![]() .
.
Таблиця 1. Значення функції
| xi | yi |
| 1,50 | 15,132 |
| 1,55 | 17,422 |
| 1,60 | 20,393 |
| 1,65 | 23,994 |
| 1,70 | 28,160 |
| 1,75 | 32,812 |
| 1,80 | 37,857 |
Розв’язання:
Складемо спочатку таблицю кінцевих різниць (табл. 2).
Таблиця 2. Кінцеві різниці
| і | xi | yi | yi | 2yi | 3yi |
| 2,290 | -0,051 | ||||
| 1 | 1,55 | 17,422 | 2,971 | 0,630 | -0,065 |
| 2 | 1,60 | 20,393 | 3,601 | 0,565 | -0,079 |
| 3 | 1,65 | 23,994 | 4,166 | 0,486 | -0,093 |
| 4 | 1,70 | 28,160 | 4,652 | 0,393 | |
| 5 | 1,75 | 32,812 | 5,045 | ||
| 6 | 1,80 | 37,857 |
При складанні таблиці різниць обмежимося різницями третього порядку, оскільки вони практично постійні.
·
За першою
інтерполяційною формулою Ньютона (1. 2. 7), приймаючи ![]() ,
, ![]() (табл. 2),
отримаємо:
(табл. 2),
отримаємо:
![]() ;
;
![]() ;
;

·
За другою
інтерполяційною формулою Ньютона (1. 2. 11), приймаючи ![]() ,
, ![]() (табл. 2),
отримаємо:
(табл. 2),
отримаємо:
![]() ;
;
![]() ;
;
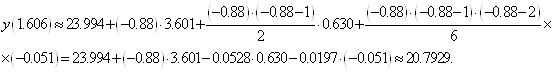
·
За першою
інтерполяційною формулою Гауса (1. 3. 4), приймаючи ![]() ,
, ![]() , матимемо:
, матимемо:
![]() .
.
Отже, отримаємо:

·
За другою
інтерполяційною формулою Гауса (1. 3. 6), приймаючи ![]() ,
, ![]() , отримаємо:
, отримаємо:
![]() ;
;
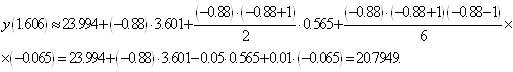
· За інтерполяційною формулою Стірлінга, підставляючи відповідні коефіцієнти із таблиці різниць (табл. 2) у формулу (1. 5. 1) отримаємо:

· За інтерполяційною формулою Бесселя, підставляючи відповідні коефіцієнти із таблиці різниць (табл. 2) в формулу (1. 4. 3) отримаємо:

Тепер проведемо оцінку отриманих результатів. Введемо наступні позначення:
ІФН – інтерполяційна формула Ньютона;
ІФГ - інтерполяційна формула Гауса;
ІФБ - інтерполяційна формула Бесселя;
ІФС - інтерполяційна формула Стірлінга.
Для зручності результати запишемо у вигляді таблиці (табл. 3):
| ІФН 1-ша | ІФН 2-га | ІФГ 1-ша | ІФГ 2-га | ІФБ | ІФС |
| 20,7930 | 20,7929 | 20,7931 | 20,79486 | 20,5784 | 20,7930 |
Таблиця 3. Отримані результати.
Тепер визначимо похибку отриманих результатів. Для цього від значення, отриманого за допомогою першої ІФН, віднімемо результати, отримані зі допомогою інших формул. В результаті отримаємо таку розрахункову табличку (табл. 4):
| ІФН 2-га | ІФГ 1-ша | ІФГ 2-га | ІФБ | ІФС |
| 0,00015 | 0,00013 | 0,00186 | 0,21457 | 0,00001 |
Таблиця 4. Абсолютні похибки результатів.
Тоді, щоб отримати відносну похибку
результату, необхідно абсолютні похибки поділити на відповідні отримані
наближені значення ![]() , отримані за формулами (1. 2. 7),
(1. 2. 11), (1. 3. 4), (1. 3. 6), (1. 4. 3), (1. 5. 1). Тобто маємо (табл. 5):
, отримані за формулами (1. 2. 7),
(1. 2. 11), (1. 3. 4), (1. 3. 6), (1. 4. 3), (1. 5. 1). Тобто маємо (табл. 5):
| ІФН 2-га | ІФГ 1-ша | ІФГ 2-га | ІФБ | ІФС |
| 0,00070% | 0,00062% | 0,00893% | 1,04270% | 0,00004% |
Таблиця 5. Відносні похибки.
Бачимо, найкраще наближення до значення, одержаного за ІФН 1-ою, досягається інтерполяційною формулою Стірлінга.
Висновок. Як зазначалося вище (див.
пункт 1.6), ІФС краще використовувати, для інтерполювання в середині таблиці, в
чому ми і переконалися в даному прикладі, оскільки ![]() знаходиться всередині таблиці.
знаходиться всередині таблиці.
Знайти значення функції ![]() ,
заданої таблицею (табл. 6) при значенню аргументу
,
заданої таблицею (табл. 6) при значенню аргументу ![]() , використовуючи
інтерполяційну формулу Ньютона для нерівновіддалених вузлів. При розрахунках
враховувати лише розділені різниці першого і другого порядків.
, використовуючи
інтерполяційну формулу Ньютона для нерівновіддалених вузлів. При розрахунках
враховувати лише розділені різниці першого і другого порядків.
Таблиця 6. Значення функції
| xi | f(xi) |
| 2,24382 | |
| 2,26446 | |
| 2,29841 | |
| 2,32221 | |
| 2,35164 | |
| 2,38690 | |
| 2,41162 | |
| 0,782 | 2,44777 |
Розв’язання:
Оскільки в умові сказано використовувати лише розділені різниці другого і третього порядку, то формула Ньютона для нерівновіддалених вузлів (1. 7. 5) матиме вигляд:
![]() ,
,
де ![]() .
.
Попередньо обчислимо необхідні значення розділених різниць (табл. 7).
Таблиця 7. Розділені різниці
| і | xi | f(xi) | f(xi,xi+1) | f(xi,xi+1,xi+2) |
| 0 | 0,698 | 2,22336 | 0,02046 | 0,00018 |
| 1 | 0,706 | 2,24382 | 0,02064 | 0,01331 |
| 2 | 0,714 | 2,26446 | 0,03395 | -0,01015 |
| 3 | 0,727 | 2,29841 | 0,02380 | 0,00563 |
| 4 | 0,736 | 2,32221 | 0,02943 | 0,00583 |
| 5 | 0,747 | 2,35164 | 0,03526 | -0,01054 |
| 6 | 0,760 | 2,38690 | 0,02472 | 0,01143 |
| 7 | 0,769 | 2,41162 | 0,03615 | |
| 8 | 0,782 | 2,44777 |
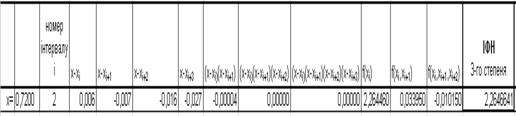
Для визначення ![]() приймаємо
приймаємо ![]() . Для
зручності складаємо допоміжну розрахункову таблицю (табл. 8), звідки отримаємо:
. Для
зручності складаємо допоміжну розрахункову таблицю (табл. 8), звідки отримаємо:
![]()
Таблиця 8. Розрахункова таблиця
1.9.1 Призначення програми
Дану програму було розроблено з метою надання можливості за допомогою ЕОМ обчислювати наближені значення функції у випадку, коли функція задана таблично, використовуючи для цього інтерполяційні формули для рівновіддалених вузлів (1. 2. 7), (1. 2. 11), (1. 3. 4), (1. 3. 6), (1. 4. 3), (1. 5. 1) та інтерполяційну формулу (1. 7. 5)- для нерівновіддалених вузлів. Крім того, враховано можливість отримання загального вигляду відповідного інтерполяційного поліному наближення з метою подальшого використання при, наприклад, плануванні експериментів в біології, фізиці, хімії, географії, медицині та ін. галузях науки.
Так як програма, більшою мірою, призначення для використання в навчальних цілях, то в ній передбачена можливість вибору початкових даних згідно варінтів лабораторних робіт, наведених в [7], що дає можливість зменшити витрати часу при введені даних для студентів.
Програмну реалізацію було здійснено в інтегрованому середовищі розробки Microsoft Visual Studio 2008 Team System у проекті типу Visual C# з використанням мови програмування С# на базі технології .NET Framework 2.0. Програма має назву «InterPolation».
Розглянемо основні процедури і функції програми та їх призначення:
![]() DeltaCount
– функція для побудови таблиці кінцевих різниць по заданим данним (вхідними
даними є введені користувачем значення функції типу double);
DeltaCount
– функція для побудови таблиці кінцевих різниць по заданим данним (вхідними
даними є введені користувачем значення функції типу double);
![]() Fact – функція для обчислення
факторіалів, необхідних для застосування формул (5), (9), (12), (13), (15), (16).
Вхідними даними для цієї функції слугує степінь полінома n, введеного користувачем, яка має тип
integer;
Fact – функція для обчислення
факторіалів, необхідних для застосування формул (5), (9), (12), (13), (15), (16).
Вхідними даними для цієї функції слугує степінь полінома n, введеного користувачем, яка має тип
integer;
![]() EvalNewtonNerivni – функція, яка
перевіряє, чи вузли інтерполяції є рівновіддаленими, чи нерівновіддаленим. У
випадку нерівновіддалених вузлів обчислює наближене значення функції за
формулою (20). Дана функція використовує вже написану функцію DeltaCount, для отримання
необхідних для формули данних.
EvalNewtonNerivni – функція, яка
перевіряє, чи вузли інтерполяції є рівновіддаленими, чи нерівновіддаленим. У
випадку нерівновіддалених вузлів обчислює наближене значення функції за
формулою (20). Дана функція використовує вже написану функцію DeltaCount, для отримання
необхідних для формули данних.
![]() EvalFFNewton – функція, яка застосовує
першу інтерполяційну формулу Ньютона згідно з введеними даними і використовуючи
функцію DeltaCount та функцію Fact. Результатом її виконання буде
наближене значення функції згідно формули (5) типу double;
EvalFFNewton – функція, яка застосовує
першу інтерполяційну формулу Ньютона згідно з введеними даними і використовуючи
функцію DeltaCount та функцію Fact. Результатом її виконання буде
наближене значення функції згідно формули (5) типу double;
![]() FFNewton – функція, що виводить
формулу (5) і обчислене згідно функції EvalFFNewton наближення функції;
FFNewton – функція, що виводить
формулу (5) і обчислене згідно функції EvalFFNewton наближення функції;
![]() EvalSFNewton - функція, яка застосовує
другу інтерполяційну формулу Ньютона згідно з введеними даними і використовуючи
функцію DeltaCount та функцію Fact. Результатом її виконання буде наближене значення функції згідно формули
(9) типу double;
EvalSFNewton - функція, яка застосовує
другу інтерполяційну формулу Ньютона згідно з введеними даними і використовуючи
функцію DeltaCount та функцію Fact. Результатом її виконання буде наближене значення функції згідно формули
(9) типу double;
![]() FFNewton – функція, що виводить
формулу (9) і обчислене згідно функції EvalSFNewton наближення функції;
FFNewton – функція, що виводить
формулу (9) і обчислене згідно функції EvalSFNewton наближення функції;
Аналогіно відповідно працють функції EvalFFGauss і FFGauss для першої формули Гауса, EvalSFGauss і SFGauss для другої формули Гауса, EvalFStirling і FStirling для формули Стірлінга та EvalFBessel і FBessel для формули Бесселя.
![]() GetX0 – функція для визначення умовного
нуля
GetX0 – функція для визначення умовного
нуля ![]() відповідно
до формул, які застосовуються, тобто тут також використовується функція DeltaCount;
відповідно
до формул, які застосовуються, тобто тут також використовується функція DeltaCount;
![]() PaintPlot – функція для побудови
графіку. В даному випадку сам графік будується в електронній таблиці Excel, результат імпортується в С# і відбувається вивід у вікно
програми;
PaintPlot – функція для побудови
графіку. В даному випадку сам графік будується в електронній таблиці Excel, результат імпортується в С# і відбувається вивід у вікно
програми;
![]() WhereIsX – функція, яка визначає, де
знаходиться х у таблиці кінцевих різниць (ближче до початку, кінця чи до середени)
і відповідно до того як написано вище в теоретичній частині у випадку, коли
користувач забуде обрати формулу для обчислень, сама обирає, яку формулу краще застосовувати;
WhereIsX – функція, яка визначає, де
знаходиться х у таблиці кінцевих різниць (ближче до початку, кінця чи до середени)
і відповідно до того як написано вище в теоретичній частині у випадку, коли
користувач забуде обрати формулу для обчислень, сама обирає, яку формулу краще застосовувати;
Тобто це основні функції та процедури, окрім них в програмі ще використовуються допоміжні функції для зчитування даних, для перевірки правильності введених даних, для зберігання результатів у файл, для запуску тестового прикладу, який розглядався в пункті 1.8.1 і т.д.
1.9.3 Інструкція по використанню програми
Для запуску програми «InterPolation» потрібно відкрити папку Release і запустити InterPolation.ехе. В результаті з’явиться вікно програми (мал. 2).
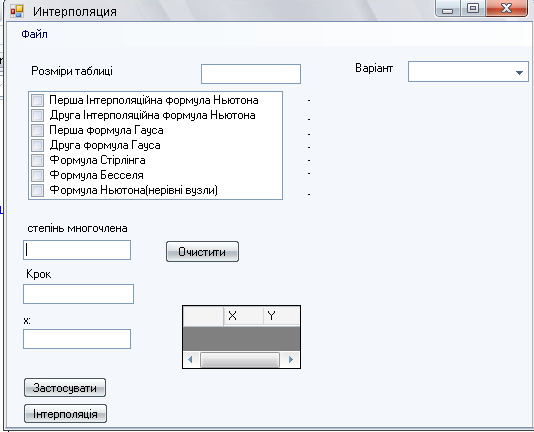
Мал. 2. Інтерфейс основної форми програми
У полі «х» вводиться значення аргументу, для якого необхідно наближено обчислити значення функції, заданої відповідною таблицею. У полі «степінь многочлена» користувачеві необхідно ввести степінь многочленна для наближення функції. У поле «крок» потрібно ввести крок h, а в полі «Розміри таблиці» вводиться кількість даних фіксованих значень функції. Потім у відповідному віконці обирається формула, яка застосовується для наближення. Після цього натискаємо кнопку «Застосувати» і у вікні ще з’являється табличка для вводу хі, уі. Після заповнення таблиці потрібно натиснути кнопку «Інтерполяція» для того, щоб програма виконала необхідні обчислення і видала результат. Крім того, з правого боку є випадаючий список «Варіант», де користувач може обрати один із 30-ти варіантів вихідних даних, що містяться в [7], потім знову ж таки обрати степінь полінома, х, формули, які хоче застосовувати. В меню «Файл» користувач може обрати «Тестовий варіант». В результаті програма виведе всі результати обчислень згідно прикладу 1 (пункт 1.8.1) (мал. 3):
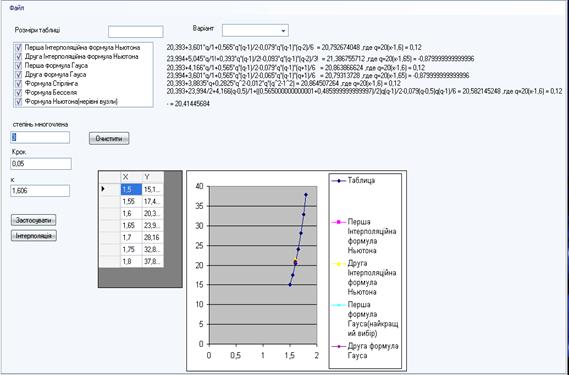
Мал. 3. Тестовий варіант
В меню файл користувач також може обрати «Зберегти». В результаті програма збереже результати роботи програми у файл. Тип файлу визначає сам користувач. Тобто, якщо, наприклад, зберегти результати обчислень тестового варіанту у текстовому документі, то відкривши цей файл будемо мати наступне (мал. 4):

Мал. 4. Лістинг результатів
1.9.4 Перевірка працездатності програми
Покажемо працездатність програми на
прикладі 1 (пункт 1.8.1). Для цього можна самостійно ввести всі необхідні дані
або обрати в меню файл, як зазначалося вище, пункт «тестовий варіант». Як видно
з результатів, отриманих при застосуванні програми (мал. 3), всі формули дають майже
однакове наближення, окрім формули Бесселя (дану формулу краще використовувати
при ![]() ). Особливо добре це видно з
графіка. Тепер порівняємо отриманий результат із розрахунками, отриманими за
допомогою електронної таблиці Excel (див. мал. 5).
). Особливо добре це видно з
графіка. Тепер порівняємо отриманий результат із розрахунками, отриманими за
допомогою електронної таблиці Excel (див. мал. 5).
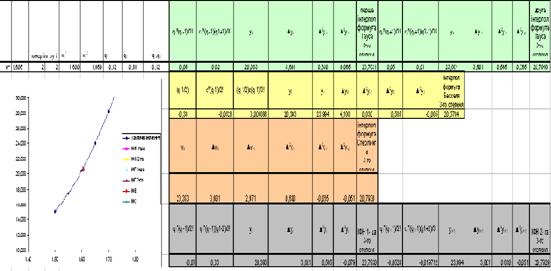
Мал. 5. Результати обчислень в електронній таблиці Excel
Тобто бачимо, що отримані результати дещо відрізняються (на 0,01). Це пов’язано з тим, що в електронній таблиці менша точність обчислень, ніж у програмі. Однак, збільшуючи степінь полінома отримаємо практично однакові результати.
Код програми в додатку 1.
1. Ильин В.А., Позняк Э. Г., Основы математического анализа, ч. II.- М.: Наука, 1980, с.50
2. Демидович Б. П., Марон И. А., Основы вычеслительной математики, Наука, 1970.
3. http://miest.narod.ru
4. Копченова Н.В., Марон И.А. – Вычислительная математика в примерах и задачах. «Наука» Москва, 1972г.
5. Турчак Л.И. – Основы численных методов. «Наука» Москва, 1987г.
6. Вержбицкий В. М., Численные методы. Математический анализ и обыкновенные дифференциальные уравнения. «Высшая школа» Москва, 2001
7. Воробьева Г. Н., Данилова А. Н. Практикум по вычислительной матиматике, изд.-II, «Высшая школа», Москва, 1990
8. Калиткин Н. П., Численные методы. - М.: Наука, 1978
9. Полия Г., Сеге Г. Теория функций (специальная часть).- М., 1978
10. Буслов В.А., Яковлев С.Л. Численные методы ІІ. Решение уравнений. Курс лекций. Санкт-Петербург, 2001
11. Бахвалов Н.С., Жидков Н.П., Кобельников Г.М. - Численные методы, М., Наука, 1987
12. Хаусхолдер А. С., Основы численного анализа.-М., 1953