
Рефераты по рекламе
Рефераты по философии
Рефераты по финансам
Рефераты по химии
Рефераты по цифровым устройствам
Рефераты по экологическому праву
Рефераты по экономико-математическому моделированию
Рефераты по экономической географии
Рефераты по экономической теории
Рефераты по этике
Рефераты по юриспруденции
Рефераты по языковедению
Рефераты по юридическим наукам
Рефераты по истории
Рефераты по компьютерным наукам
Рефераты по медицинским наукам
Рефераты по финансовым наукам
Рефераты по управленческим наукам
Рефераты по строительным наукам
Психология педагогика
Промышленность производство
Биология и химия
Языкознание филология
Издательское дело и полиграфия
Рефераты по краеведению и этнографии
Рефераты по религии и мифологии
Рефераты по медицине
Рефераты по сексологии
Рефераты по москвоведению
Рефераты по экологии
Краткое содержание произведений
Рефераты по физкультуре и спорту
Топики по английскому языку
Рефераты по математике
Рефераты по музыке
Остальные рефераты
Контрольная работа: Потрійний інтеграл
Контрольная работа: Потрійний інтеграл
ПОТРІЙНИЙ ІНТЕГРАЛ
1. Поняття потрійного інтеграла. Умови його існування та властивості
Схема побудови потрійного інтеграла така сама, як і звичайного визначеного інтеграла та подвійного інтеграла.
Нехай функція ![]() визначена в
обмеженій замкненій області
визначена в
обмеженій замкненій області ![]() . Розіб'ємо область
. Розіб'ємо область ![]() сіткою поверхонь на
сіткою поверхонь на ![]() частин
частин ![]() , які не мають спільних внутрішніх точок
і об'єми яких дорівнюють
, які не мають спільних внутрішніх точок
і об'єми яких дорівнюють ![]() . У кожній частині
. У кожній частині ![]() візьмемо довільну точку
візьмемо довільну точку
![]() і
утворимо суму
і
утворимо суму
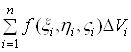 ,(1)
,(1)
яка називається інтегральною
сумою для функції ![]() за областю
за областю ![]() . Нехай
. Нехай ![]() – найбільший з діаметрів областей
– найбільший з діаметрів областей ![]() .
.
Якщо інтегральна
сума (1) при ![]() має скінченну границю, яка не
залежить ні від способу розбиття області
має скінченну границю, яка не
залежить ні від способу розбиття області ![]() на частини
на частини ![]() , ні від вибору в них
точок
, ні від вибору в них
точок ![]() , то
ця границя називається потрійним інтегралом і позначається одним із таких
символів:
, то
ця границя називається потрійним інтегралом і позначається одним із таких
символів:
![]() або
або ![]() .
.
Таким чином, за означенням
 ,(2)
,(2)
де ![]() – функція, інтегровна в
області
– функція, інтегровна в
області ![]() ;
; ![]() – область
інтегрування;
– область
інтегрування; ![]() і
і ![]() – змінні інтегрування;
– змінні інтегрування; ![]() (або
(або ![]() ) – елемент
об'єму.
) – елемент
об'єму.
Якщо по тілу ![]() розподілено
масу з об'ємною густиною
розподілено
масу з об'ємною густиною ![]() в точці
в точці ![]() , то маса
, то маса ![]() цього тіла знаходиться за
формулою
цього тіла знаходиться за
формулою
![]() . (3)
. (3)
Формула (3)
аналогічна формулі (1.8) і може розглядатися як механічний зміст потрійного
інтеграла, коли підінтегральна функція невід'ємна в області ![]() . Якщо всюди в області
покласти
. Якщо всюди в області
покласти ![]() ,
то з формули (2) випливає формула для обчислення об'єму
,
то з формули (2) випливає формула для обчислення об'єму ![]() тіла
тіла ![]() :
:
![]() .(4)
.(4)
Потрійний інтеграл є безпосереднім узагальненням подвійного інтеграла на тривимірний простір. Теорія потрійного інтеграла аналогічна теорії подвійного інтеграла, тому в більшості випадків ми обмежимося лише формулюваннями тверджень і короткими поясненнями.
Теорема (достатня умова інтегровності
функції). Якщо функція ![]() неперервна в обмеженій замкненій
області
неперервна в обмеженій замкненій
області ![]() ,
то вона в цій області інтегрована.
,
то вона в цій області інтегрована.
Властивості потрійних інтегралів.
1. Сталий множник можна винести за знак потрійного інтеграла:
![]() .
.
Потрійний інтеграл від суми кількох інтегровних функцій дорівнює сумі потрійних інтегралів від доданків:
![]() .
.
3. Якщо в області
інтегрування ![]() , то
, то
![]() .
.
4. Якщо функції ![]() та
та ![]() визначені в
одній і тій самій області
визначені в
одній і тій самій області ![]() і
і ![]() , то
, то
![]() .
.
5. (Адитивність
потрійного інтеграла.) Якщо область інтегрування ![]() функції
функції ![]() розбити на частини
розбити на частини ![]() і
і ![]() , які не мають спільних
внутрішніх точок, то
, які не мають спільних
внутрішніх точок, то
![]() .
.
6. (Оцінка
потрійного інтеграла.) Якщо функція ![]() неперервна в обмеженій замкненій
області
неперервна в обмеженій замкненій
області ![]() ,
яка має об'єм
,
яка має об'єм ![]() , то
, то
![]() ,
,
де ![]() і
і ![]() відповідно найменше і
найбільше значення функції
відповідно найменше і
найбільше значення функції ![]() в області
в області ![]() .
.
7. (Середнє
значення функції.) Якщо функція ![]() неперервна в обмеженій замкненій
області
неперервна в обмеженій замкненій
області ![]() ,
яка має об'єм
,
яка має об'єм ![]() , то в цій області існує така
точка
, то в цій області існує така
точка ![]() , що
, що
![]() .
.
Величина
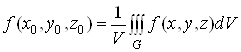
називається середнім
значенням функції ![]() в області
в області ![]() .
.
2. Обчислення потрійного інтеграла
Обчислення потрійного інтеграла зводять до обчислення повторних, тобто до інтегрування за кожною змінній окремо.
Нехай область ![]() обмежена знизу
і зверху поверхнями
обмежена знизу
і зверху поверхнями ![]() і
і ![]() , а з боків циліндричною
поверхнею, твірні якої паралельні осі
, а з боків циліндричною
поверхнею, твірні якої паралельні осі ![]() . Позначимо проекцію області
. Позначимо проекцію області ![]() на площину
на площину ![]() через
через ![]() (рис. 1) і
вважатимемо, що функції
(рис. 1) і
вважатимемо, що функції ![]() і
і ![]() неперервні в
неперервні в ![]() .
.
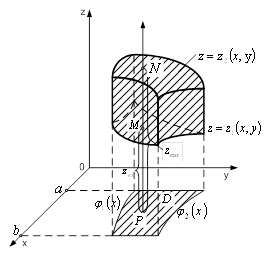
Рисунок 1 – Область ![]()
Якщо при цьому
область ![]() є
правильною, то область
є
правильною, то область ![]() називається правильною у напрямі
осі
називається правильною у напрямі
осі ![]() . Припустимо,
що кожна пряма, яка проходить через кожну внутрішню точку
. Припустимо,
що кожна пряма, яка проходить через кожну внутрішню точку ![]() паралельно осі
паралельно осі ![]() , перетинає
межу області
, перетинає
межу області ![]() у точках
у точках ![]() і
і ![]() . Точку
. Точку ![]() назвемо точкою входу в область
назвемо точкою входу в область ![]()
![]() , а точку
, а точку ![]() – точкою виходу з
області
– точкою виходу з
області ![]() ,
а їхні аплікати позначимо відповідно через
,
а їхні аплікати позначимо відповідно через ![]() і
і ![]() . Тоді
. Тоді ![]() ,
, ![]() і для будь-якої неперервної в
області
і для будь-якої неперервної в
області ![]() функції
функції
![]() має місце
формула
має місце
формула
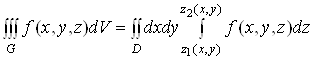 .(5)
.(5)
Зміст формули (5)
такий. Щоб обчислити потрійний інтеграл, потрібно спочатку обчислити інтеграл 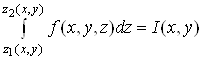 за змінною
за змінною ![]() , вважаючи
, вважаючи ![]() та
та ![]() сталими.
Нижньою межею цього інтеграла є апліката точки
сталими.
Нижньою межею цього інтеграла є апліката точки ![]() входу
входу ![]() , а верхньою – апліката
, а верхньою – апліката ![]() точки виходу
точки виходу ![]() . Внаслідок
інтегрування отримаємо функцію
. Внаслідок
інтегрування отримаємо функцію ![]() від змінних
від змінних ![]() та
та ![]() .
.
Якщо область ![]() , наприклад,
обмежена кривими
, наприклад,
обмежена кривими ![]() і
і ![]()
![]() , де
, де ![]() і
і ![]() – неперервні функції, тобто
– неперервні функції, тобто
![]() , то, переходячи від
подвійного інтеграла
, то, переходячи від
подвійного інтеграла ![]() до повторного (п. 1.3), отримаємо
формулу
до повторного (п. 1.3), отримаємо
формулу
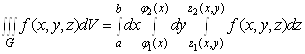 ,(6)
,(6)
яка зводить
обчислення потрійного інтеграла до послідовного обчислення трьох визначених
інтегралів. Порядок інтегрування може бути й іншим, тобто змінні ![]() і
і ![]() у правій частині
формули (6) за певних умов можна міняти місцями.
у правій частині
формули (6) за певних умов можна міняти місцями.
Якщо, наприклад,
область ![]() правильна
в напрямі осі
правильна
в напрямі осі ![]() :
:
![]() ,
,
де ![]() – неперервні функції, то
– неперервні функції, то
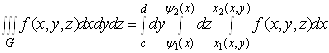 .
.
Зокрема, якщо областю інтегрування є паралелепіпед:
![]() ,
,
то
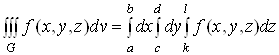 . (7)
. (7)
У цьому разі
інтегрування виконується в будь-якому порядку, оскільки область ![]() правильна у напрямі
всіх трьох координатних осей
правильна у напрямі
всіх трьох координатних осей ![]() .
.
3. Заміна змінних в потрійному інтегралі
Заміну змінної в
потрійному інтегралі виконують за таким правилом: якщо обмежена замкнена
область ![]() взаємно
однозначно відображується на область
взаємно
однозначно відображується на область ![]() за допомогою неперервно
диференційовних функцій
за допомогою неперервно
диференційовних функцій ![]() ,
, ![]() ,
, ![]() , якобіан
, якобіан ![]() в області
в області ![]() не дорівнює нулю:
не дорівнює нулю:

і ![]() – неперервна в
– неперервна в ![]() , то справедлива формула
, то справедлива формула
![]() . (8)
. (8)
На практиці
найуживанішими є циліндричні та сферичні координати. При переході від
прямокутних координат ![]() до циліндричних
до циліндричних ![]() (рис.4, а), пов'язаних
з
(рис.4, а), пов'язаних
з ![]() співвідношеннями
співвідношеннями
![]() ;
;
![]() ,
,
якобіан перетворення
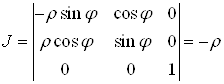 .
.
З формули (8) отримуємо потрійний інтеграл у циліндричних координатах:
![]() .(9)
.(9)
Назва
«циліндричні координати» пов'язана з тим, що координатна поверхня ![]() є циліндром,
прямолінійні твірні якого паралельні осі
є циліндром,
прямолінійні твірні якого паралельні осі ![]() .
.
При переході від
прямокутних координат ![]() до сферичних
до сферичних ![]()
(рис. 4, б), які
пов'язані з ![]() формулами
формулами
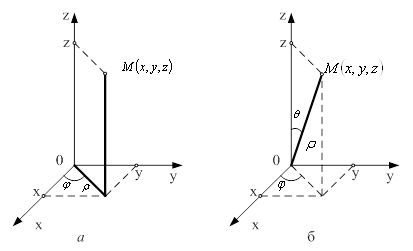
Рисунок 4 – Координати: а) циліндричні; б) сферичні
![]() ;
;
![]() ,
,
якобіан перетворення
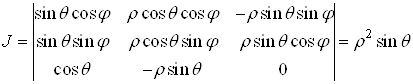 .
.
З формули (8) знаходимо потрійний інтеграл у сферичних координатах:
![]() . (10)
. (10)
Назва «сферичні
координати» пов'язана з тим, що координатна поверхня ![]() є сферою. При обчисленні
потрійного інтеграла в циліндричних чи сферичних координатах область
є сферою. При обчисленні
потрійного інтеграла в циліндричних чи сферичних координатах область ![]() , як правило,
не будують, а межі інтегрування знаходять безпосередньо за областю
, як правило,
не будують, а межі інтегрування знаходять безпосередньо за областю ![]() , користуючись
геометричним змістом нових координат. При цьому рівняння поверхонь
, користуючись
геометричним змістом нових координат. При цьому рівняння поверхонь ![]() та
та ![]() , які обмежують
область
, які обмежують
область ![]() ,
записують у нових координатах.
,
записують у нових координатах.
Зокрема, якщо
область ![]() обмежена
циліндричною поверхнею
обмежена
циліндричною поверхнею ![]() та площинами
та площинами ![]() , то всі межі
інтегрування в циліндричній системі координат сталі:
, то всі межі
інтегрування в циліндричній системі координат сталі:
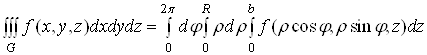
і не змінюються
при зміні порядку інтегрування. Те саме буде у сферичних координатах у випадку,
коли ![]() –
куля:
–
куля: ![]() або
кульове кільце. Наприклад, якщо
або
кульове кільце. Наприклад, якщо ![]() – кульове кільце з внутрішньою
сферою
– кульове кільце з внутрішньою
сферою ![]() , то
рівняння цієї сфери в сферичних координатах має вигляд
, то
рівняння цієї сфери в сферичних координатах має вигляд
![]()
або
![]() ,
,
звідки ![]() . Аналогічно
. Аналогічно ![]() – рівняння
зовнішньої сфери, тому
– рівняння
зовнішньої сфери, тому
![]() .
.
У випадку, коли ![]() – куля
– куля ![]() , у цій
формулі слід покласти
, у цій
формулі слід покласти ![]() . Інших будь-яких загальних
рекомендацій, коли необхідно переходити до тієї чи іншої системи координат,
дати неможливо. Це залежить і від області інтегрування, і від підінтегральної
функції. Іноді потрібно написати інтеграл у різних системах координат і лише
після цього вирішити, в якій з них обчислення буде найпростішим.
. Інших будь-яких загальних
рекомендацій, коли необхідно переходити до тієї чи іншої системи координат,
дати неможливо. Це залежить і від області інтегрування, і від підінтегральної
функції. Іноді потрібно написати інтеграл у різних системах координат і лише
після цього вирішити, в якій з них обчислення буде найпростішим.
Приклад
1. Обчислити
інтеграл ![]() ,
якщо область
,
якщо область ![]() обмежена поверхнями
обмежена поверхнями ![]() і
і ![]() .
.
Розв’язання
Область ![]() є конусом
(рис. 5).
є конусом
(рис. 5).
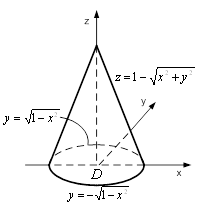
Рисунок 5 – Область ![]()
Рівняння конічної
поверхні, яка обмежує область ![]() , можна записати у вигляді
, можна записати у вигляді ![]() , а саму
область
, а саму
область ![]() подати
таким чином:
подати
таким чином: ![]() , де
, де ![]() – круг радіуса
– круг радіуса ![]() з центром
з центром ![]() . Тому даний
потрійний інтеграл можна звести до послідовного обчислення трьох визначених
інтегралів у прямокутних координатах:
. Тому даний
потрійний інтеграл можна звести до послідовного обчислення трьох визначених
інтегралів у прямокутних координатах:
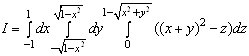 .
.
Проте зручніше
перейти до циліндричних координат ![]() . Тоді прообраз круга
. Тоді прообраз круга ![]() є прямокутник
є прямокутник ![]() , прообраз
конічної поверхні – плоска поверхня
, прообраз
конічної поверхні – плоска поверхня ![]() , а прообраз області
, а прообраз області ![]() – область
– область ![]() . Якобіан
переходу до циліндричних координат дорівнює
. Якобіан
переходу до циліндричних координат дорівнює ![]() , підінтегральна функція в
циліндричних координатах дорівнює
, підінтегральна функція в
циліндричних координатах дорівнює![]() . Зводячи потрійний інтеграл за
областю
. Зводячи потрійний інтеграл за
областю ![]() до
послідовного обчислення трьох визначних інтегралів, отримаємо
до
послідовного обчислення трьох визначних інтегралів, отримаємо
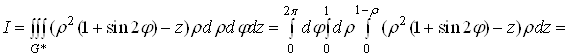
![]()
Зазначимо, що
розставлення меж інтегрування в циліндричних координатах, як правило, виконують,
розглядаючи не область ![]() , а зміну циліндричних координат в
області
, а зміну циліндричних координат в
області ![]() . Наочно видно, що в області
. Наочно видно, що в області ![]() змінна
змінна ![]() змінюється від
змінюється від ![]() до
до ![]() , при кожному значенні
, при кожному значенні ![]() змінна
змінна ![]() змінюється від
змінюється від ![]() до
до ![]() , а для кожної точки
, а для кожної точки ![]() області
області ![]() змінна
змінна ![]() змінюється в області
змінюється в області ![]() від
від ![]() (значення
(значення ![]() в області
в області ![]() ) до
) до ![]() (значення
(значення ![]() на конічній
поверхні).
на конічній
поверхні).
4. Деякі застосування потрійного інтеграла
інтеграл потрійний обчислення змінний
1. Обчислення об'ємів. Якщо деяке тіло є обмеженою і замкненою
областю ![]() , що має об'єм
, що має об'єм ![]() , то згідно з
формулою (4)
, то згідно з
формулою (4)
![]() .(11)
.(11)
Застосування у
механіці. Нехай ![]() – обмежена
замкнена область простору
– обмежена
замкнена область простору ![]() , яку займає деяке матеріальне
тіло з густиною
, яку займає деяке матеріальне
тіло з густиною ![]() , де
, де ![]() – неперервна функція в області
– неперервна функція в області ![]() , тоді:
, тоді:
а)маса цього тіла
![]() ;(12)
;(12)
б)моменти інерції
![]() тіла
відносно координатних осей
тіла
відносно координатних осей ![]() відповідно дорівнюють
відповідно дорівнюють
![]() . (13)
. (13)
Моменти інерції ![]() тіла відносно
координатних площин
тіла відносно
координатних площин ![]() обчислюються за формулами
обчислюються за формулами
![]() .(14)
.(14)
Момент інерції тіла відносно початку координат
![]()
![]() (15)
(15)
в) статичні
моменти ![]() тіла
відносно координатних площин
тіла
відносно координатних площин ![]() обчислюються за формулами
обчислюються за формулами
![]() ;(16)
;(16)
г) координати ![]() центра маси
тіла визначаються за формулами
центра маси
тіла визначаються за формулами
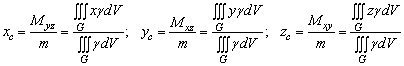 . (17)
. (17)
Доведення формули (11), як уже зазначалося, випливає з означення потрійного інтеграла:
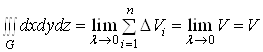 .
.